 |

 |

| LastUpdate 2024/04/17 |
| @wfq`odrxâwe u
xÍAÖĚŽđăüˇéžŻĹA˘ĆŕČPÉOtđ`˘ÄľÜ¤DGČt[\tgĆľÄLźĹˇB @ZĚwĚöĆĹQÖĚOtĚwąđˇéęAÎ\đ쏾AŔW˝ĘÉ_đvbgľÄAČßçŠČČüĹ_Ć_đńĹOtđ`ŠšéąĆŠçnßܡB @@wfq`odrxâwe u xÍAÖĚŽđăüˇéžŻĹOtđ`˘ÄľÜ¤˝ßAťąÉÍÎ\đ쏾A_đvbgľÄAČßçŠČČüĹÔ´oÍŮĆńÇ čÜšńB @ľŠľAÎ\đ쏾A_đvbgľÄAČßçŠČČüĹÔ´oĹOtđ`ąĆđRs [^ăĹŕÂ\ɡéĚŞA˝żŞúíćgÁĢéu\vZ\tgwd xvČĚšB @ß]Ě éö§Ě}ŮÉsÁ˝ĆŤAud ĹwÔâłľ˘w@(OpÖŠç÷ĎŞÜĹ)@űü´KvEn粪ę@¤@I[Đ oĹvƢ¤{đôRŠÂŻÜľ˝Bwd xđgÁ˝ÖĚOtĚ`ŤűâAńĚlŚűŞÜłÉwd xĚRs[@\ťĚŕĚĹ éąĆÉCĂŠšçęéLqđŠľÜľ˝B @Ü˝AÚĚPQ`PSĚuV~ [VvAufĆŽSvAuÉűöŽvĹÍAwd xđg¤ĆąńČąĆÜĹōľܤƢ¤ąĆđĐîľÜľ˝BĽńA§íľÄÝÄžł˘BźĚąĆÉŕpĹŤé͸šB @gÉtŻÄŮľ˘´oâZ\EmŻĚá˘ÉćÁÄA@wfq`odrxAwe u xAwd xđg˘ŞŻéąĆĹAćčřĘĚ éöĆđgݧÄéąĆŞĹŤéĆlŚÜˇB@ |
| http://kn-makkun.com/MakkunWp/excels.html |
| No | Ú@ |
| P | @QÖ |
| Q | @OpÖ |
| R | @wÖ |
| S | @ÎÖ |
| T | @˘ë˘ëČČü |
| U | @÷ŞiťĚPj |
| V | @÷ŞiťĚQj |
| W | @ĎŞ |
| X | @ń |
| PO | @Ąf |
| PP | @˝űŞĚp |
| PQ | @V~ [V @ |
| PR | @fĆŽS@ |
| PS | @ÉűöŽ@ |
| PT | @_E[h@ |
| PU | @Tvf[^Ěg˘ű |
| gbvy[WÖßé |
| @ÚÖ@ |
| @yPOPz QÖ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@|S@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{P@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B20đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@aPQOQ@đźpĹü͡éB @@@@@@@ZD12É@QaPQOQ@đźpĹü͡éB @@@@@@@ZE12É@RaPQOQ@đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C20đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč5.0 @@@@@@¨ Âśé @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 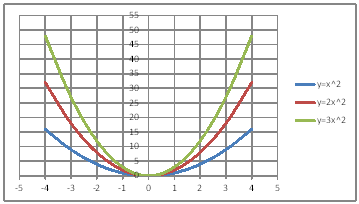 @@@l@P @@@@@@ @@@l@Q @@@@@@ |
| @yPOQz QÖ |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yPOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@ (2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč5.0 @@@@@@¨ Âśé @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ @@@@@@ 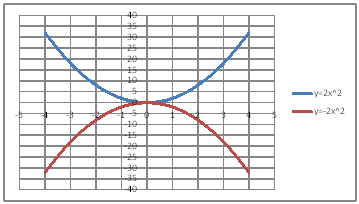 @@@@@@ @@@l@P @@@@@@ @@@l@Q @@@@@@ @@@@@ÇĚć¤ÉČÁĢéĆžŚéŠB |
| @yPORz QÖ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yPOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč5.0 @@@@@@¨ Âśé @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 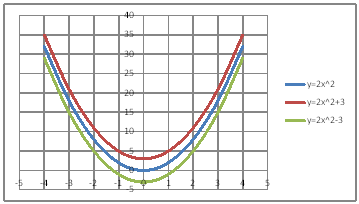 @@@l@P @@@@@@@ @@@@@@ärľČł˘B @@@l@Q @@@@@@@ @@@@@@q×Čł˘B @@@l@R @@@@@@@ @@@@@@ÇĚć¤ÉČÁĢéĆžŚéŠB |
| @yPOSz QÖ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yPOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč5.0 @@@@@@¨ Âśé @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 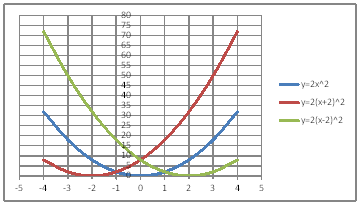 @@@l@P @@@@@@@ @@@@@@ärľČł˘B @@@l@Q @@@@@@@ @@@@@@q×Čł˘B @@@l@R @@@@@@@ @@@@@@ÇĚć¤ÉČÁĢéĆžŚéŠB |
| @yPOTz QÖ |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yPOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 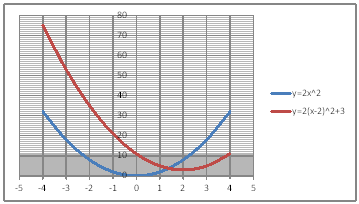 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@l@R @@@@@@@ @@@@@@ÇĚć¤ÉČÁĢéĆžŚéŠB |
| @yPOUz QÖ |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yPOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@(3) OAĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 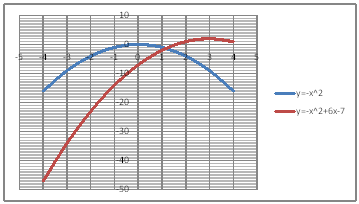 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ |
| @ÚÖ@ |
| @yQOPz OpÖ Ć Q Ć R ĚOtđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@rhm(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@rhm(q`ch`mr(QaPQ))@đźpĹü͡éB @@@@@@@ZE12É@rhm(q`ch`mr(RaPQ))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 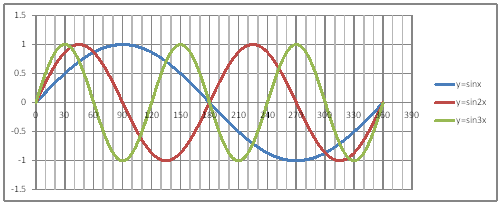 @@@l@P @@@@@@@@ĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@QĚOtĚüúđOtŠçßČł˘B@ @@@l@R @@@@@@@@RĚOtĚüúđOtŠçßČł˘B@ @@@l@S @@@@@@@@ęĘÉAĚOtĚüúÉ¢ÄAÇĚć¤ČąĆŞžŚéŠB |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B372đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@rhm(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@rhm(q`ch`mr(aPQ^Q))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C372đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D372đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 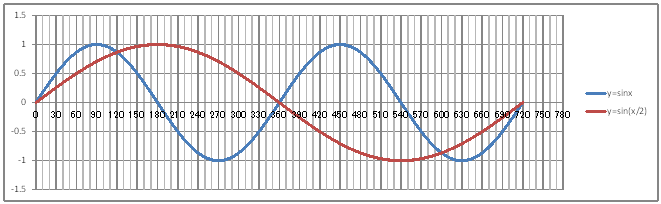 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ęĘÉA @@@@@@@ @ |
| @yQORz OpÖ Ć Q Ć R ĚOtđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@rhm(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@Qrhm(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZE12É@Rrhm(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 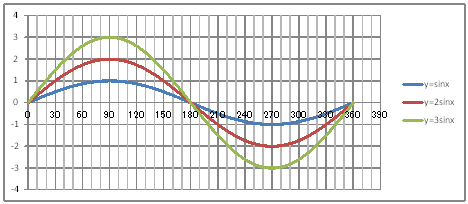 @@@l@P @@@@@@@@QĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@RĚOtĚüúđOtŠçßČł˘B@ @@@l@R @@@@@@@@ ĚOtĆ Q ĚOtĆ R ĚOtĚ @@@@@@@á˘đq×Čł˘B@ @@@l@S @@@@@@@@ęĘÉAĚOtĚUÉ¢ÄAÇĚć¤ČąĆŞžŚéŠB |
| @yQOSz OpÖ Q(|UO) ĚOtđ`B | ||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B222đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@Qrhm(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@Qrhm(q`ch`mr(aPQ|UO))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C222đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D222đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 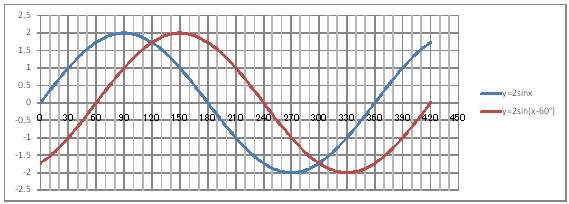 @@@l@ @@@@@@@Q(|UO) ĚOtÍAQ ĚOtđ˛űüÉ{UOžŻA @@@@@@˝sÚŽľ˝ŕĚĹ éąĆđmŠßČł˘B |
| @yQOTz OpÖ Ć Q Ć R ĚOtđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@bnr(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@bnr(q`ch`mr(QaPQ))@đźpĹü͡éB @@@@@@@ZE12É@bnr(q`ch`mr(RaPQ))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 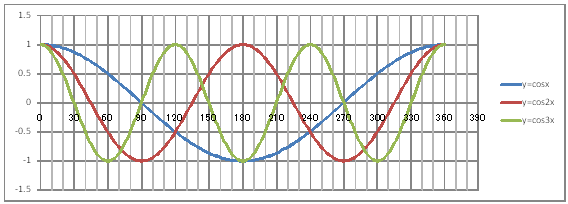 @@@l@P @@@@@@@@ĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@QĚOtĚüúđOtŠçßČł˘B@ @@@l@R @@@@@@@@RĚOtĚüúđOtŠçßČł˘B@ @@@l@S @@@@@@@@ęĘÉAĚOtĚüúÉ¢ÄAÇĚć¤ČąĆŞžŚéŠB |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B372đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@bnr(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@bnr(q`ch`mr(aPQ^Q))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C372đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D372đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 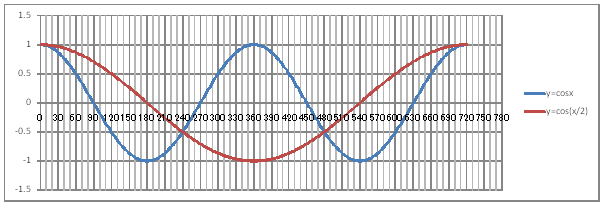 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ęĘÉA @@@@@@@ |
| @yQOVz OpÖ Ć Q Ć R ĚOtđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@bnr(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@Qbnr(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZE12É@Rbnr(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 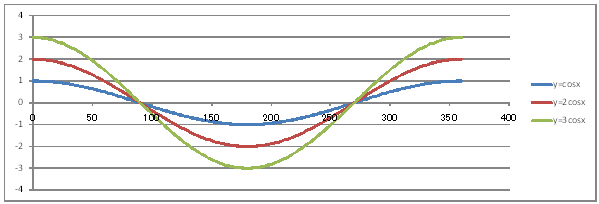 @@@l@P @@@@@@@@QĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@RĚOtĚüúđOtŠçßČł˘B@ @@@l@R @@@@@@@@ ĚOtĆ Q ĚOtĆ R ĚOtĚ @@@@@@@á˘đq×Čł˘B@ @@@l@S @@@@@@@@ęĘÉAĚOtĚUÉ¢ÄAÇĚć¤ČąĆŞžŚéŠB |
| @yQOWz OpÖ Q({UO) ĚOtđ`B | ||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@|UO@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B222đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@Qbnr(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZD12É@Qbnr(q`ch`mr(aPQ{UO))@đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C222đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D222đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 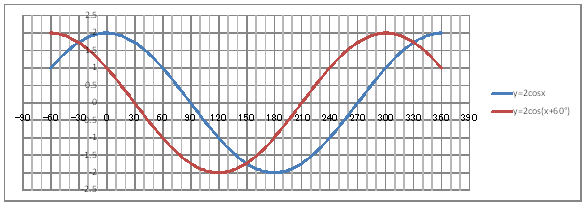 @@@l@ @@@@@@@Q({UO) ĚOtÍAQ ĚOtđ˛űüÉ|UOžŻA @@@@@@˝sÚŽľ˝ŕĚĹ éąĆđmŠßČł˘B |
| @yQOXz OpÖ x ĚOtđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |PWOđźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B56đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZB58É |WWđźpĹü͡éB @@@@@@@ZB59ÉAaTW{Q@đźpĹü͡éB @@@@@@@ZB59đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB60:B146đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZB148É XQ đźpĹü͡éB @@@@@@@ZB149ÉAaPSW{Q@đźpĹü͡éB @@@@@@@ZB149đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB150:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@s`m(q`ch`mr(aPQ))@đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľ Ä\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 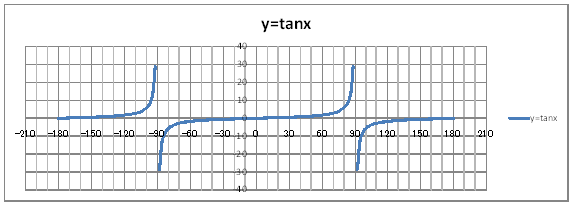 @@@l@P @@@@@@@@ĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@źü XOA|XOŞQßüÉČÁĢéąĆđmŠß Čł˘B@ |
| @yQPOz OpÖ Qx ĚOtđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |XOđźpĹü͡éB @@@@@@@ZB13ÉAaPQ{P@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B56đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZB58É |SSđźpĹü͡éB @@@@@@@ZB59ÉAaTW{P@đźpĹü͡éB @@@@@@@ZB59đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB60:B146đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZB148É SU đźpĹü͡éB @@@@@@@ZB149ÉAaPSW{P@đźpĹü͡éB @@@@@@@ZB149đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB150:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12És`m(q`ch`mr(QaPQ))đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľ Ä\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAOtGAđ @@@@@@@@śEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč15.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč5.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 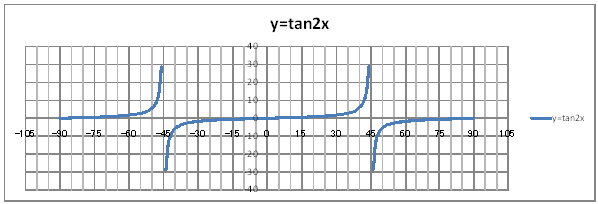 @@@l@P @@@@@@@@QĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@źü STA|STŞQßüÉČÁĢéąĆđmŠßČł˘B@ @@@l@R @@@@@@@@ęĘÉAĚOtĚüúÉ¢ÄAÇĚć¤ČąĆŞžŚéŠB |
| @yQPPz OpÖ x Ć Q ĚOtđ`B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@@@@@Ql @@@@@@@@@@yQOXzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[Aă[Ćş[đťęźęhbOľÄAO @@@@@@@@tGAđăşśEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč15.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč5.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@ B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 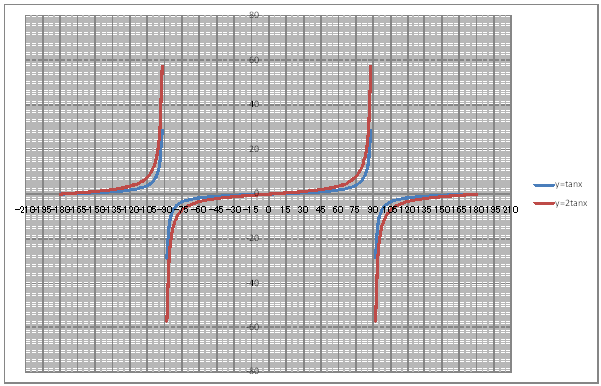 @@@l@P @@@@@@@@QĚOtĚüúđOtŠçßČł˘B@ @@@l@Q @@@@@@@@ Ć QĚOtĚĘuÖWÉ¢Äq×Čł˘B@ @@@l@R @@@@@@@@ęĘÉA Ć ĚOtĚĘuÖWÉ¢Äq×Čł˘B@ |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@@@@@Ql @@@@@@@@@@yQOXzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C372đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[Aă[Ćş[đťęźęhbOľÄAO @@@@@@@@tGAđăşśEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 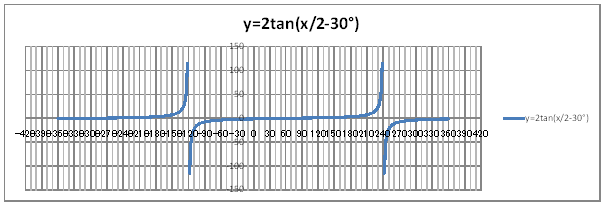 @@@l@P @@@@@@@ @@@@@@ @@@l@Q @@@@@@@ @@@@@@ |
| @yQPRz 0
360ĚĆŤA @@@@@@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@O@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É@O@đźpĹü͡éB @@@@@@@ZD13ÉAcPQ{Q@đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@bnr(q`ch`mr(QaPQ)){Qrhm(q`ch`mr(aPQ)){Q@ @@@@@@đźpĹü͡éB @@@@@@@ZE12É@|Qrhm(q`ch`mr(aPQ))OQ{Qrhm(q`ch`mr(aPQ)){R@ @@@@@@đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAśEÉLΡB @@@@@@C ăL(1)ĚÎ\ĚZĚÍÍD11:E192đhbOľÄIđˇéB @@@@@@D m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@E OtGAĚś[ĆE[đťęźęhbOľÄAśEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđťęźęŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 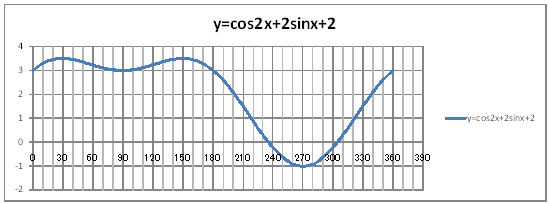 @@@@@@ 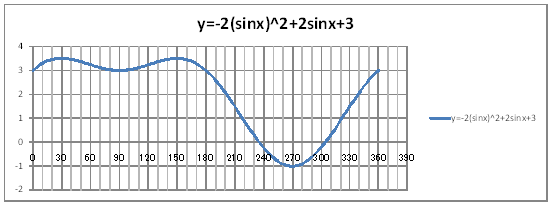 @@@l@ @@@@@@@ @@@@@@ĚOtÍŻśĹ éąĆđmŠßČł˘B |
| @yQPSz 0
360ĚĆŤA @@@@@@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@QlsăĚ[NV[gĚüÍű@t @@@@@@ZB12É@O@đźpĹü͡éB @@@@@@ZB13ÉAaPQ{Q@đźpĹü͡éB @@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@ZD12É@O@đźpĹü͡éB @@@@@@ZD13ÉAcPQ{Q@đźpĹü͡éB @@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@ZĚÍÍD14:D192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@ZC12É@rhm(q`ch`mr(aPQ)){bnr(q`ch`mr(aPQ))@ @@@@@đźpĹü͡éB @@@@@@ZE12É@rpqs(Q)rhm(q`ch`mr(aPQ{ST))@đźpĹü͡éB @@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@ZĚÍÍE13:E192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľÄAśEÉLΡB @@@@@@C ăL(1)ĚÎ\ĚZĚÍÍD11:E192đhbOľÄIđˇéB @@@@@@D m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@E OtGAĚś[ĆE[đťęźęhbOľÄAśEÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđťęźęŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč30.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 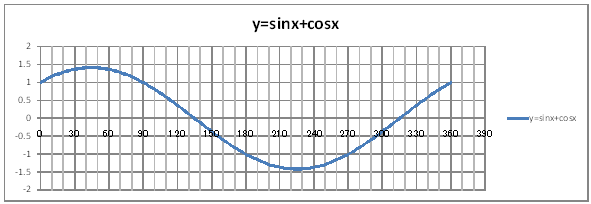 @@@@@@ 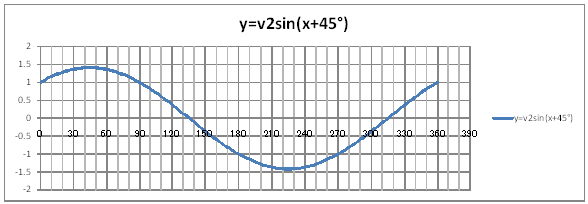 @@@l@ @@@@@@@{ Ć @@@@@@mŠßČł˘B |
| @ÚÖ@ |
| @yROPz |
|||||||||||||||||||||||||||||||||||
| @ @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É@|Q@đźpĹü͡éB @@@@@@@ZB13ÉAaPQ{P@đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B16đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É@onvdq(QCaPQ)@đźpĹü͡éB @@@@@@@ZD12É@onvdq(RCaPQ)@đźpĹü͡éB @@@@@@@ZE12É@onvdq(SCaPQ)@đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C16đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E16đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 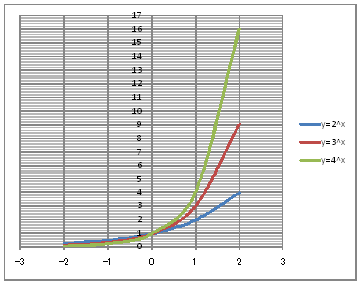 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@l@R @@@@@@@ |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yROPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E16đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 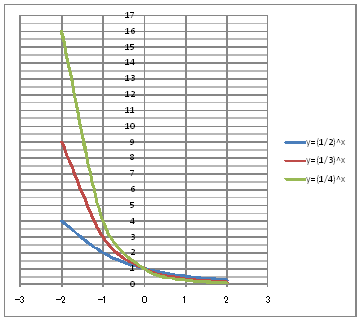 @@@l@P @@@@@@@ @@@@@@đßČł˘B @@@l@Q @@@@@@@ @@@@@@Čł˘B @@@l@R @@@@@@@ |
@č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yROPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D18đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 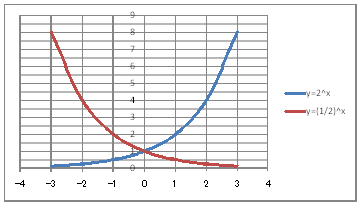 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@@@@˘éĆžŚéŠB |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@yROPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E18đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč5.0 @@@@@@¨ Âśé @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 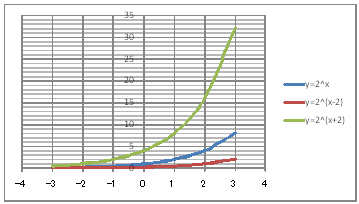 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@@@@ĆžŚéŠB |
| @č @@@@@@@@ @@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yROPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč10.0 @@@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 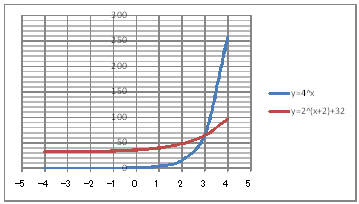 @@@l@ @@@@@@ @@@@@ |
| @č @@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@yROPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D16đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 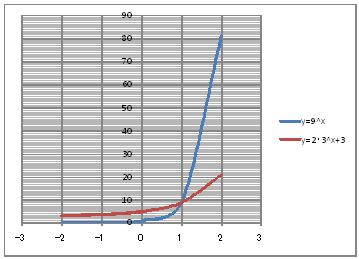 @@@l@ @@@@@@ @@@@@@ @ |
| @yROVz |
||||||||||||
| @č @@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12AB13AB14ÉAăĚ[NV[gĚć¤Éü͡éB @@@@@@@ZC12ÉAonvdq(WCP^S) đźpĹü͡éB @@@@@@@ZC13ÉAonvdq(PUCP^R) đźpĹü͡éB @@@@@@@ZC14ÉAonvdq(USCP^T) đźpĹü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB12:C14đhbOľÄIđˇéB @@@@@@A m}ün¨mc_n¨m2-Dc_ĚWc_nđś¸ŘŻ¸ˇéB @@@@@@  @@@l@ @@@@@@ @@@@@@ |
| @ÚÖ@ |
| @ySOPz ÎÖ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB12:B20đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@@ŞŢŠçlđIđľAŹ_ČşĚ đTɡéB @@@@@@@ZB12É 1/16 đźpĹü͡éBiŹĹ\Śłęéj @@@@@@@ZĚÍÍB13:B20ÉAăĚ[NV[gĚć¤ÉźpĹü͡éB @@@@@@@ZC12É knf(aPQCQ) đźpĹü͡éB @@@@@@@ZD12É knf(aPQCR) đźpĹü͡éB @@@@@@@ZE12É knf(aPQCS) đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C20đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 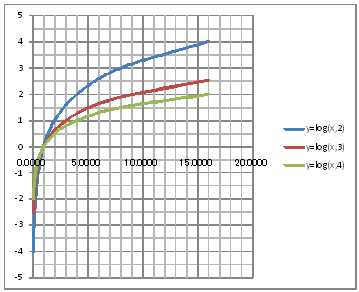 @@@l@P @@@@@@@ @@@@@@¤ĘľÄĘé_ĚŔWđßČł˘B @@@l@Q @@@@@@@ @@@@@@¤ĘˇéQßüđßČł˘B @@@l@R @@@@@@@ @@@@@@á˘đq×Čł˘B @ |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@ySOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 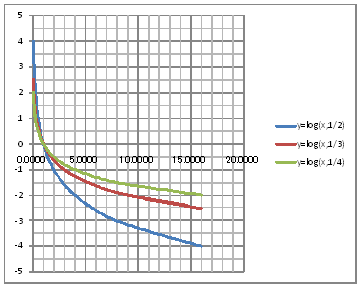 @@@l@P @@@@@@@ @@@@@@¤ĘľÄĘé_ĚŔWđßČł˘B @@@l@Q @@@@@@@ @@@@@@¤ĘˇéQßüđßČł˘B @@@l@R @@@@@@@ @@@@@@á˘đq×Čł˘B @ |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@ySOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@ 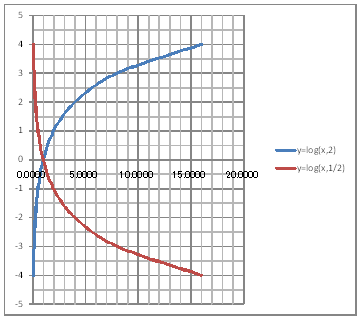 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@@@@ÇĚć¤ÉČÁĢéĆžŚéŠB |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@ySOPzĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@  @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@@@@ÇĚć¤ÉČÁĢéĆžŚéŠB @ |
| @ySOTz |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@@y401zĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D20đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.1 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@  @@@l@ @@@@@@@ @@@@@@ |
| @ySOUz |
||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@y401zĚ[NV[gĚüÍű@đQƾĞł˘B
@@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D18đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝üĆ}[J[nđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľÄAOtGAđ @@@@@@@@ăşÉLΡB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.1 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@(4) OtŠçÎ\Ě_(}[J[)đÁˇéB @@@@@@@ OtGAđś¸ŘŻ¸ľÄANeBuɡéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@  @@@l@ @@@@@@@ @@@@@@@ @@@@@@ |
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12AB13AB14ÉAăĚ[NV[gĚć¤Éü͡éB @@@@@@@ZĚÍÍC12:C14đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@ ŞŢŠçlđIđľAŹ_ČşĚ đTɡéB @@@@@@@ZC12ÉAP^Q đźpĹü͡éB @@@@@@@ZC13ÉA|Pknf(P^RCQ) đźpĹü͡éB @@@@@@@ZC14ÉAknf(VCP^Q) đźpĹü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB12:C14đhbOľÄIđˇéB @@@@@@A m}ün¨mc_n¨m2-Dc_ĚWc_nđś¸ŘŻ¸ˇéB @@@@@@  @@@l@ @@@@@@@ @@@@@@ |
| @ÚÖ@ |
| @yTOPz |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |X đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B132đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É S{SQRT(RU|(aPQ{R)OQ) đźpĹü͡éB @@@@@@@ZD12É S|SQRT(RU|(aPQ{R)OQ) đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C132đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D132đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 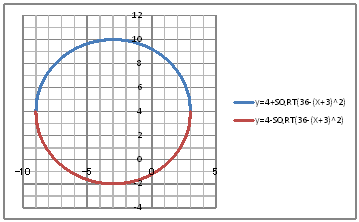 @@@l@ @@@@@@@S(|RCS)AźaUĚ~ÉČÁĢéąĆđmFľČł˘B @ |
| yTOQz |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |QDQRU đźpĹü͡éB @@@@@@@ZB13É |QDQ đźpĹü͡éB @@@@@@@ZB14É aPR{ODP đźpĹü͡éB @@@@@@@ZB14đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB15:B57đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZB58É QDQRU đźpĹü͡éB @@@@@@@ZC12É SQRT(T|aPQOQ) đźpĹü͡éB @@@@@@@ZD12É |SQRT(T|aPQOQ) đźpĹü͡éB @@@@@@@ZE12É |aPQ{P đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C58đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E58đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 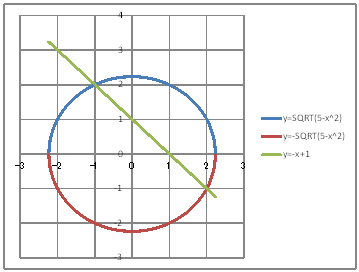 @@@l@ @@@@@@@ @@@@@@¤L_ĚŔWđßČł˘B @ |
| yTORz Qč_(RCO)A(|RCO)ŠçĚŁĚaŞPOĹ éČ~đ`B | ||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@R @@@@@@@@@@QPOćčAT @@@@@@@@@@ @@@@@@@@@@S @@@@@@@@@@ćÁÄA @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |T đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B112đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É SSQRT(P|aPQOQ^QT) đźpĹü͡éB @@@@@@@ZD12É |SSQRT(P|aPQOQ^QT) đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C112đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D112đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 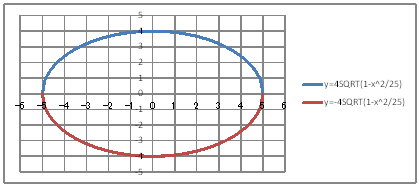 @@@l@ @@@@@@@ |
| yTOSz č_(QCO)Aźü |Q ŠçĚŁŞľ˘ú¨üđ`B | ||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É O đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B52đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É QSQRT(QaPQ) đźpĹü͡éB @@@@@@@ZD12É |QSQRT(QaPQ) đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C52đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D52đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 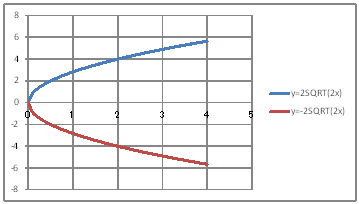 @@@l@ @@@@@@@ |
| @yTOTz Qč_(TCO)A(|TCO)Šç̡̣ŞUĹ éoČüđ`B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@TAQUA @@@@@@@@@@ćÁÄA @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É PO đźpĹü͡éB @@@@@@@ZB13É aPQ|ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B82đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZB84É |R đźpĹü͡éB @@@@@@@ZB85É aWS|ODP đźpĹü͡éB @@@@@@@ZB85đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB86:B154đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É SSQRT(aPQOQ^X|P) đźpĹü͡éB @@@@@@@ZD12É |SSQRT(aPQOQ^X|P) đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C154đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@y504zđQĆ @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 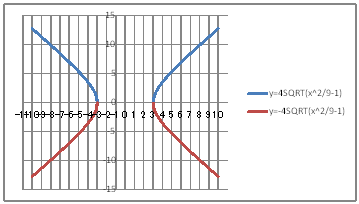 @@@l@ @@@@@@@ |
| @ÚÖ@ |
| @yUOPz |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |R đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B72đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É |QaPQOR{UaPQ{P đźpĹü͡éB @@@@@@@ZD12É |UaPQOQ{U đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbNľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C72đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D72đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 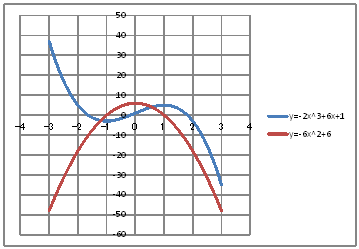 @@@l@P @@@@@@@ @@@l@Q @@@@@@@ @@@l@R @@@@@@@ @ |
| yUOQz @@@@@ĹĺlĆĹŹlđßéB |
|||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |Q đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B72đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É QaPQOR|RaPQOQ|PQaPQ|U đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C72đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C72đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 1.0 @@@@@@¨ Âśé ¨ ˛ĚđENbN ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč 1.0 @@@@@@¨ Âśé ¨ ˛ĚđENbN ¨ âÚˇüĚÇÁ @@@@@@B ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 5.0 @@@@@@¨ Âśé @@@@@@ 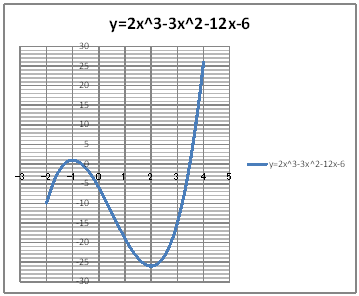 @@@l@P @@@@@@@|Q S ĚĆŤĚĹĺlđOtŠçßČł˘B @@@l@Q @@@@@@@|Q S ĚĆŤĚĹŹlđOtŠçßČł˘B @ |
| yUORz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB8É đü͡éB @@@@@@@ZC8É P đźpĹü͡éB @@@@@@@ZB12É |Q đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B72đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQOR|RaPQOQ đźpĹü͡éB @@@@@@@ZD12É bW đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbOľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C72đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:D72đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč 1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 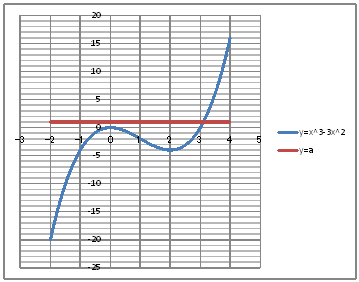 @@@l@P @@@@@@@PA|T@ĚĆŤAŮČéŔđĚÂđßČł˘B @@@l@Q @@@@@@@OA|S@ĚĆŤAŮČéŔđĚÂđßČł˘B @@@l@R @@@@@@@|Q@ĚĆŤAŮČéŔđĚÂđßČł˘B @@@l@S @@@@@@@ŮČéŔđĚÂÍAčĚlÉćÁÄÇĚć¤ÉĎíéŠB |
| yUOSz |
|||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É O đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B44đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQOR|RaPQOQ{S đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C44đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C44đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 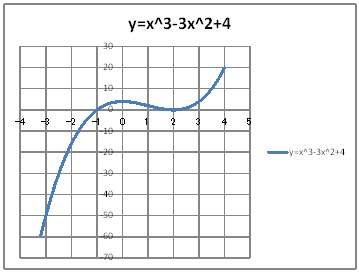 @@@l@ @@@@@@@O ĚĆŤA @@@@@@@ @ |
| @yUOTz Čü ĚOtĆAťĚăĚ_o(PCO)ɨŻéÚüĆ@üđ`B | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@Úü F |OPi|Pj@@@@@|P @@@@@@@@@@@ü F |O|Pi|Pj@@ @|{P @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É ODOT đźpĹü͡éB @@@@@@@ZB13É aPQ{ODOT đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B111đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É km(aPQ) đźpĹü͡éB @@@@@@@ZD12É aPQ|P đźpĹü͡éB @@@@@@@ZE12É |aPQ{P đźpĹü͡éB @@@@@@@ZĚÍÍC12:E12đhbOľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C111đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E111đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 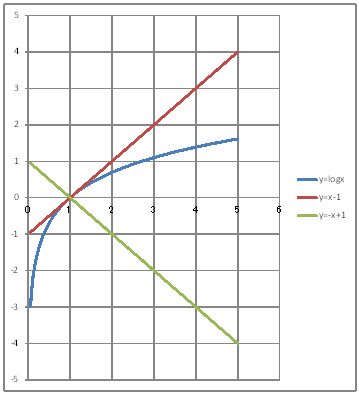 @@@l@P @@@@@@@|P Ş ăĚ_(PCO)ɨŻéÚüÉČÁĢéąĆđmŠßČł˘B @@@l@Q @@@@@@@|{P Ş ăĚ_(PCO)ɨŻé@üÉČÁĢéąĆđmŠßČł˘B |
| @č @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |Q đźpĹü͡éB @@@@@@@ZB13É aPQ{ODOT đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B92đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É rpqs(P|aPQOQ^S) đźpĹü͡éB @@@@@@@ZD12É |rpqs(P|aPQOQ^S) đźpĹü͡éB @@@@@@@ZE12É |RaPQ^W{T^S đźpĹü͡éB @@@@@@@ZÍÍC12:E12đhbOľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C92đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:E92đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚś[ĆE[Aă[Ćş[đđťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 1.0 ¨ Âśé @@@@@@¨ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč 0.2¨ Âśé @@@@@@¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč @@@@@@¨ âÚˇÔu Ĺč 0.2 ¨ Âśé ¨ ˛ĚđENbN @@@@@@¨ âÚˇüĚÇÁ @@@@@@ 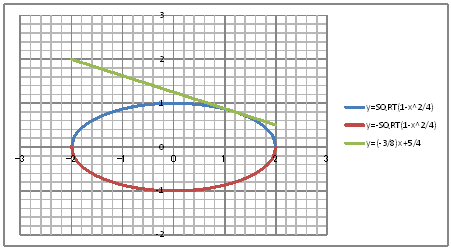 @@@l@ @@@@@@@ @@@@@@ČÁĢéąĆđmŠßČł˘B |
| @ÚÖ@ |
| @yVOPz |
|||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |R đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B72đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQrpqs(X|aPQOQ) đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C72đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C72đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč1.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@A ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ âÚˇÔu Ĺč0.5 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ âÚˇüĚÇÁ @@@@@@ 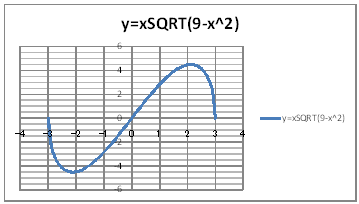 @@@l@P @@@@@@@OtŠçÉĺlđßČł˘B @@@l@Q @@@@@@@OtŠçÉŹlđßČł˘B @@@l@R @@@@@@@OtŠçĹĺlđßČł˘B @@@l@S @@@@@@@OtŠçĹŹlđßČł˘B @ |
| yVOQz O QΠɨ˘ÄAÖ {Q ĚOtđ`B | |||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É O đźpĹü͡éB @@@@@@@ZB13É aPQ{Q đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É @@@@@@@@q`ch`mr(aPQ){QSIN(q`ch`mr(aPQ)) đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C192đhbOľÄIđˇéB@ @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ˛ĚŽÝč ¨ ÚˇÔu Ĺč 60.0 @@@@@@¨ Âśé ¨ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 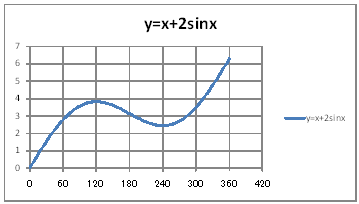 @@@l@P @@@@@@@O QΠɨŻéÉĺlđĆéĆŤĚĚlđOtđpľÄßA @@@@@@ÉĺlđvZľČł˘B @@@l@Q @@@@@@@O QΠɨŻéÉŹlđĆéĆŤĚĚlđOtđpľÄßA @@@@@@ÉŹlđvZľČł˘B @@@l@R @@@@@@@O QΠɨŻéĹĺlđĆéĆŤĚĚlđOtđpľÄßA @@@@@@ĹĺlđvZľČł˘B @@@l@S @@@@@@@O QΠɨŻéĹŹlđĆéĆŤĚĚlđOtđpľÄßA @@@@@@ĹŹlđvZľČł˘B @ |
| yVORz |
|||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |Q đźpĹü͡éB @@@@@@@ZB13É aPQ{ODP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B52đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQ{rpqs(S|aPQOQ) đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C52đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC52É Q đźpĹü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C52đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 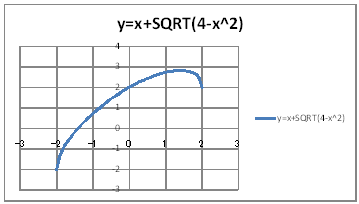 @@@l@ @@@@@@@OtŠçĹŹlĆťĚĆŤĚĚlđßČł˘B |
| yVOSz |
|||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É |P đźpĹü͡éB @@@@@@@ZB13É aPQ{ODOT đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B52đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É dwo(QaPQ)|Qdwo(aPQ){P đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C52đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB11:C52đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@@@@ 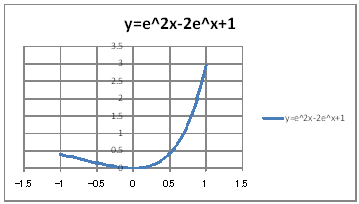 @@@l@P @@@@@@@|P P ĚĆŤĚĹĺlĆťĚĆŤĚĚlđOtđpľÄßČł˘B @@@l@Q @@@@@@@|P P ĚĆŤĚĹŹlĆťĚĆŤĚĚlđOtđpľÄßČł˘B @ |
| @ÚÖ@ |
| @yWOPz |
||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É ODOP đźpĹü͡éB @@@@@@@ZB13É aPQ{ODOP đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B111đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQOQ đźpĹü͡éB @@@@@@@ZD12É ODOPbPQ đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C111đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçćŞĎđßéB @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍD12:D111ĚađßéB @@ @@@@@@[NV[gĚZD112É rtl(cPQFcPPP) đźpĹü͡éB @@@l@P @@@@@@@ĚčĎŞđvZľÄAČü @@@@@@ßČł˘B @@@@@@@ @@@l@Q @@@@@@@l@PĹß˝čĎŞĚlĆA[NV[gĚÎ\ĚZĚÍÍD12:D111 @@@@@@ĚaĹ éZcPPQĚlđärľČł˘B @ |
| @yWOQz TCNCh |AP| (O QÎ)ĚOtđ`BÜ˝AťĚˇłđßéB | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É O đźpĹü͡éB @@@@@@@ZB13É aPQ{Q đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É @@@@@@@@q`ch`mr(aPQ)|SIN(q`ch`mr(aPQ)) đźpĹü͡éB @@@@@@@ZD12É @@@@@@@@P|COS(q`ch`mr(aPQ)) đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbOľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C192đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE13É bPR|bPQ đźpĹü͡éB @@@@@@@ZF13É cPR|cPQ đźpĹü͡éB @@@@@@@ZG13É rpqs(dPROQ{ePROQ) đźpĹü͡éB @@@@@@@ZĚÍÍE13:G13đhbOľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE14:E192đhbNľAENbNľÄ\čtŻđIđˇéB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍC11:D192đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨m˝ünđś¸ŘŻ¸ˇéB @@@@@@B OtGAĚă[Ćş[đťęźęhbOľLkľÄ˛ŽˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚđE¸ŘŻ¸ ¨ ÚˇüĚÇÁ @@@(4) ăL(1)ĚÎ\ŠçTCNCh̡łđßéB @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍG13:G192ĚađßéB @@ @@@@@@[NV[gĚZG193É rtl(fPRFfPXQ) đźpĹü͡éB @@@@@@ 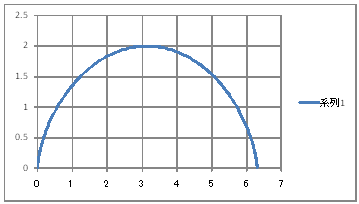 @@@l@P @@@@@@@ĚčĎŞđvZľÄATCNCh |AP| (O QÎ) @@@@@@̡łđßČł˘B @@@@@@@ 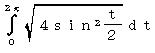 @@@l@Q @@@@@@@l@PĹß˝čĎŞĚlĆA[NV[gĚÎ\ĚZĚÍÍG13:G192 @@@@@@ĚaĹ éZfPXRĚlđärľČł˘B @ |
| @ÚÖ@ |
| @yXOPz ćRŞTAćPQŞTXĹ éˇńĚęĘđßéB | |||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@@ĆAđA§ľÄđĆA|VAU @@@@@@@@@@ćÁÄA @@@@@@@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B111đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É UaPQ|PR đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C111đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@P @@@@@@@ @@@@@@@PSRŞćQUĹ éąĆđ[NV[gĹmFľČł˘B @@@l@Q @@@@@@@ @@@@@@ćXUŞTURĹ éąĆđ[NV[gĹmFľČł˘B @ |
| @yXOQz ćRŞPQAćVŞPXQĹ éäńĚęĘđßéB | ||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@@ĆAđA§ľÄđĆARA}Q @@@@@@@@@@ćÁÄA @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:D11Éă\Ěć¤Éü͡éB @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É RQO(aPQ|P) đźpĹü͡éB @@@@@@@ZD12É R(|Q)O(aPQ|P) đźpĹü͡éB @@@@@@@ZĚÍÍC12:D12đhbOľAENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@P @@@@@@@ @@@@@@@ @@@@@@@ćWŞRWSĆ|RWSĹ éąĆđ[NV[gĹmFľČł˘B @@@l@Q @@@@@@@ @@@@@@@ @@@@@@@VWUSRQŞćPXĹ éąĆđ[NV[gĹmFľČł˘B @ |
| @yXORzŞTOAöˇŞ|U̡ńĚŠçćÜĹĚađßéB | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:E11đhbNľAENbNľÄZĚŽđIđˇéB @@@@@@\`Ž ¨ ŞŢĚśń ¨ nj đIđˇéB @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B61đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É |UaPQ{TU đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C61đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É TO đźpĹü͡éB @@@@@@@ZD13É cPQ{bPR đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D61đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É |RaPQOQ{TRaPQ đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E61đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@P @@@@@@@[NV[gDńĚaĆEńĚ -3n^2+53n ŞęvľÄ˘éąĆđmŠßČł˘B @@@l@Q @@@@@@@ @@@@@@@ @@@@@@@ćÁÄAX ĚĆŤAĹĺÉČéB @@@@@@@X ĚĆŤĹĺĹ éąĆđ[NV[gĹmFľČł˘B |
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É QO(aPQ|Q) đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É ODT đźpĹü͡éB @@@@@@@ZD13É cPQ{bPR đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D46hbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É (QOaPQ|P)^Q đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E46đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@P @@@@@@@[NV[gDńĚaĆEńĚ (2^n-1)/2 ŞęvľÄ˘éąĆđmŠßČł˘B @@@l@Q @@@@@@@ @@@@@@@ąęđđ˘ÄAPP ÉČéB @@@@@@@aŞßÄPOOOđ´ŚéĚÍAćPPÜĹĚaĹ éąĆđ[NV[gĹ @@@@@@mFľČł˘B @ |
| @yXOTz |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQOQ đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É P đźpĹü͡éB @@@@@@@ZD13É cPQ{bPR đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D46hbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É aPQ(aPQ{P)(QaPQ{P)^U đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E46đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@ @@@@@@@[NV[gDńĚaĆEńĚ n(n+1)(2n+1)/6 ŞęvľÄ˘éąĆđmŠßČł˘B |
| @yXOUz |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É aPQOR đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É P đźpĹü͡éB @@@@@@@ZD13É cPQ{bPR đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D46hbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É (aPQ(aPQ{P)^Q)OQ đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E46đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@ @@@@@@@[NV[gDńĚaĆEńĚ {n(n+1)/2}^2 ŞęvľÄ˘éąĆđmŠßČł˘B |
| @yXOVzĚńĚęĘđßéB @@@@@@RCSCUCPOCPWCRSCEEE |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC13É QO(aPR|Q) đźpĹü͡éB @@@@@@@ZC13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC14:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É R đźpĹü͡éB @@@@@@@ZD13É cPQ{bPR đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D46hbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É QO(aPQ|P){Q đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E46đhbNľAENbNľÄ\čtŻđIđˇéB @@@l@ @@@@@@@[NV[gDńĚaĆEńĚ 2^(n-1)+2 ŞęvľÄ˘éąĆđmŠßČł˘B |
| @yXOWzĚQťŽĹčßçę˝ń{}ĚęĘđßéB @@@@@@ @@@@@@ |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É P đźpĹü͡éB @@@@@@@ZC13É QbPQ{R đźpĹü͡éB @@@@@@@ZC13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC14:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É QO(aPQ{P)|R đźpĹü͡éB @@@@@@@ZD12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD13:D46hbNľAENbNľÄ\čtŻđIđˇéB @@@l@ @@@@@@@[NV[gCńĚQťŽĆDńĚ 2^(n+1)-3 ŞęvľÄ˘éąĆđmŠßČł˘B |
| @yXOXz @@@@@@@@ @@@@@@@@ @@@@@@@@ |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@ąĚQťŽđđ˘ÄęĘđßéĆA @@@@@@@@@@ 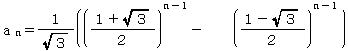 @ĆČéB @ĆČéB@@@@@@@@@@ @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É O đźpĹü͡éB @@@@@@@ZC13É P đźpĹü͡éB @@@@@@@ZC14É (QbPR{bPQ)^Q đźpĹü͡éB @@@@@@@ZC14đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC15:C46đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É @@@@@@@@(((1+SQRT(3))/2)^(B12-1)-((1-SQRT(3))/2)^(B12-1))/SQRT(3) @@@@@@@đźpĹü͡éB @@@@@@@ZD12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD13:D46hbNľAENbNľÄ\čtŻđIđˇéB @@@l@ @@@@@@@[NV[gCńĚQťŽĆDńĚęĘ ŞęvľÄ˘éąĆđmŠß Čł˘B |
| @yXPOz ĚQťŽĹčßçę˝tB{ib`ńđlŚéB @@@@@@@ @@@@@@@ @@@@@@@ |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É P đźpĹü͡éB @@@@@@@ZB13É aPQ{P đźpĹü͡éB @@@@@@@ZB13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍB14:B61đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZC12É P đźpĹü͡éB @@@@@@@ZC13É P đźpĹü͡éB @@@@@@@ZC14É bPQ{bPR đźpĹü͡éB @@@@@@@ZC14đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC15:C61đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD13É bPR^bPQ đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D61hbNľAENbNľÄ\čtŻđIđˇéB @@@l@ @@@@@@@ @@@@@@ÉߢąĆđmŠßČł˘B |
| @ÚÖ@ |
| @y1001z OpÖĚtÖ Ć Ęx@Šçx@ÖĚϡ @@@@@@i`rhmÖA`bnrÖA`s`mÖAcdfqddrÖj |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB12:B20đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@@\Ś`Ž ¨ ŞŢĚśń ¨ nj đIđˇéB @@@@@@@ZĚÍÍB12:B20ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZĚÍÍD12:D20đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@@\Ś`Ž ¨ ŞŢĚśń ¨ nj đIđˇéB @@@@@@@ZĚÍÍD12:D20ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZĚÍÍF12:F20đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@@\Ś`Ž ¨ ŞŢĚśń ¨ nj đIđˇéB @@@@@@@ZĚÍÍF12:F18ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC12É cdfqddr(`rhm(|P)) đü͡éB @@@@@@@ŻlÉľÄAC13ŠçC20ÜĹAcdfqddr(`rhm(ańĚŻśsĚl)) đ @@@@@@źpĹü͡éB @@@@@@@ZE12É cdfqddr(`bnr(P)) đü͡éB @@@@@@@ŻlÉľÄAE13ŠçE20ÜĹAcdfqddr(`bnr(cńĚŻśsĚl)) đ @@@@@@źpĹü͡éB @@@@@@@ZG12É cdfqddr(`s`m(|rpqs(R))) đü͡éB @@@@@@@ŻlÉľÄAG13ŠçG18ÜĹAcdfqddr(`s`m(eńĚŻśsĚl)) đ @@@@@@źpĹü͡éB @@@ÖÉÂ˘Ä @@@@@@@`rhmÖ ĽĽĽ ASIN(ŔlP) @@@@@@@@@@ŔlPÉČérhmĚpxđWAPĘĹÔˇB @@@@@@@`bnrÖ ĽĽĽ ACOS(ŔlP) @@@@@@@@@@ŔlPÉČébnrĚpxđWAPĘĹÔˇB @@@@@@@`s`mÖ ĽĽĽ ATAN(ŔlP) @@@@@@@@@@ŔlPÉČés`mĚpxđWAPĘĹÔˇB @@@@@@@cdfqddrÖ ĽĽĽ DEGREES(WA) @@@@@@@@@@WAPĘĚpxđx@ĚpxÉϡˇéB @ |
| @y1002z ĄfĚQćĚa @@@@@@irtlrpÖj |
||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:B20đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@@\Ś`Ž ¨ ŞŢĚśń ¨ nj đIđˇéB @@@@@@@ZĚÍÍB11:B20ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC12É rpqs(O) đźpĹü͡éB @@@@@@@ZC13É rpqs(P) đźpĹü͡éB @@@@@@@ZC14É rpqs(Q) đźpĹü͡éB @@@@@@@ZC15É rpqs(R) đźpĹü͡éB @@@@@@@ZC16É rpqs(S) đźpĹü͡éB @@@@@@@ZC17É rpqs(T) đźpĹü͡éB @@@@@@@ZC18É rpqs(U) đźpĹü͡éB @@@@@@@ZC19É rpqs(V) đźpĹü͡éB @@@@@@@ZC20É rpqs(W) đźpĹü͡éB @@@@@@@ZD13É rtlrp(bPQCbPR) đźpĹü͡éB @@@@@@@ZD13đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD14:D20đhbNľAENbNľÄ\čtŻđIđˇéB @@@ÖÉÂ˘Ä @@@@@@@rtlrpÖ ĽĽĽ SUMSQ(ŔlPCŔlQ) @@@@@@@@@@ @ |
| @y1003z ĄfĚlĽvZaˇĎ¤ Ć Ąf`ŽÉ\Ś @@@@@@ihlrtlÖAhlrtaÖAhloqnctbsÖAhlchuÖAbnlokdwÖj |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZC11É ` đü͡éB @@@@@@@ZC12É a đü͡éB @@@@@@@ZD11É bnlokdw(TC|R) đźpĹü͡éB @@@@@@@ZD12É bnlokdw(|QCV) đźpĹü͡éB @@@@@@@ZF11É b đźpĹü͡éB @@@@@@@ZF12É c đźpĹü͡éB @@@@@@@ZG11É bnlokdw(QCP) đźpĹü͡éB @@@@@@@ZG12É bnlokdw(QC|P) đźpĹü͡éB @@@@@@@ZĚÍÍB14:B17ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZĚÍÍC14:C17ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZD14É hlrtl(cPPCcPQ) đźpĹü͡éB @@@@@@@ZD15É hlrta(cPPCcPQ) đźpĹü͡éB @@@@@@@ZD16É hloqnctbs(cPPCcPQ) đźpĹü͡éB @@@@@@@ZD17É hlchu(fPPCfPQ) đźpĹü͡éB @@@ÖÉÂ˘Ä @@@@@@@hlrtlÖ ĽĽĽ IMSUM(ĄfPCĄfQ) @@@@@@@@@@ĄfP{ĄfQ ĚlđÔˇB @@@@@@@hlrtaÖ ĽĽĽ IMSUB(ĄfPCĄfQ) @@@@@@@@@@ĄfP|ĄfQ ĚlđÔˇB @@@@@@@hloqnctbsÖ ĽĽĽ IMPRODUCT(ĄfPCĄfQ) @@@@@@@@@@ĄfP~ĄfQ ĚlđÔˇB @@@@@@@hlchuÖ ĽĽĽ IMDIV(ĄfPCĄfQ) @@@@@@@@@@ĄfPĄfQ ĚlđÔˇB @@@@@@@bnlokdwÖ ĽĽĽ COMPLEX(ŔlPCŔlQ) @@@@@@@@@@ĄfĚ` (ŔlP){(ŔlQ) đÔˇB |
| @y1004z¤đČĄf Ć âÎl @@@@@@ihlbnmitf`sdÖAhl`arÖj |
||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZB12É R{S đźpĹü͡éB @@@@@@@ZB13É R đźpĹü͡éB @@@@@@@ZB14É R đźpĹü͡éB @@@@@@@ZC12É hlbnmitf`sd(aPQ) đźpĹü͡éB @@@@@@@ZC13É hlbnmitf`sd(aPR) đźpĹü͡éB @@@@@@@ZC14É hlbnmitf`sd(aPS) đźpĹü͡éB @@@@@@@ZD12É hl`ar(aPQ) đźpĹü͡éB @@@@@@@ZD13É hl`ar(aPR) đźpĹü͡éB @@@@@@@ZD14É hl`ar(aPS) đźpĹü͡éB @@@ÖÉÂ˘Ä @@@@@@@hlbnmitf`sdÖ ĽĽĽ IMCONJUGATE(ĄfP) @@@@@@@@@@ĄfPɤđČĄfđÔˇB @@@@@@@hl`arÖ ĽĽĽ IMABS(ĄfP) @@@@@@@@@@ĄfPĚâÎlđÔˇB @ |
| @y1005zĄfĚÎpAŔŞAŞ @@@@@@ihl`qftldmsÖAhlqd`kÖAhl`fhm`qxÖj |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:B20đhbNľAENbNľÄZĚŽÝčđIđˇéB @@@@@@\Ś`Ž ¨ ŞŢĚśń ¨ nj đIđˇéB @@@@@@@ZĚÍÍB11:B20ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC12É bnlokdw(PCO) đźpĹü͡éB @@@@@@@ZC13É bnlokdw(rpqs(R)CP) đźpĹü͡éB @@@@@@@ZC14É bnlokdw(PCP) đźpĹü͡éB @@@@@@@ZC15É bnlokdw(PCrpqs(R)) đźpĹü͡éB @@@@@@@ZC16É bnlokdw(OCP) đźpĹü͡éB @@@@@@@ZC17É bnlokdw(|PCrpqs(R)) đźpĹü͡éB @@@@@@@ZC18É bnlokdw(|PCP) đźpĹü͡éB @@@@@@@ZC19É bnlokdw(|rpqs(R)CP) đźpĹü͡éB @@@@@@@ZC20É bnlokdw(|PCO) đźpĹü͡éB @@@@@@@ZD12É cdfqddr(hl`qftldms(bPQ)) đźpĹü͡éB @@@@@@@ZD12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD13:D20đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É hlqd`k(bPQ) đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E20đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZF12É hl`fhm`qx(bPQ) đźpĹü͡éB @@@@@@@ZF12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍF13:F20đhbNľAENbNľÄ\čtŻđIđˇéB @@@ÖÉÂ˘Ä @@@@@@@hl`qftldmsÖ ĽĽĽ IMARGUMENT(ĄfP) @@@@@@@@@@ĄfP ĚÎpđWAPĘĹÔˇB @@@@@@@hlqd`kÖ ĽĽĽ IMREAL(ĄfP) @@@@@@@@@@ĄfPĚŔŞđÔˇB @@@@@@@hl`fhm`qxÖ ĽĽĽ IMAGINARY(ĄfP) @@@@@@@@@@ĄfPĚŞđÔˇB |
| @y1006z @@@@@@@@@@hEAuĚč @@@@@@@@@@@@ @@@@@@@@@@@@ihlonvdqÖj |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB @@@Ql @@@@@y401zĚ[NV[gĚüÍű@đQƾĞł˘B
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB9:B23ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC9É bnlokdw(PCrpqs(R)) đźpĹü͡éB @@@@@@@ZC11É ăĚ\Ěć¤Éü͡éB @@@@@@@ZC12É hlonvdq(bXCaPQ) đźpĹü͡éB @@@@@@@ZC12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍC13:C23đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZD12É cdfqddr(hl`qftldms(bPQ))đźpĹü͡éB @@@@@@@ZD12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍD13:D23đhbNľAENbNľÄ\čtŻđIđˇéB @@@@@@@ZE12É hl`ar(bPQ) đźpĹü͡éB @@@@@@@ZE12đENbNľÄRs[đIđˇéB @@@@@@@ZĚÍÍE13:E23đhbNľAENbNľÄ\čtŻđIđˇéB @@@ÖÉÂ˘Ä @@@@@@@hlonvdqÖ ĽĽĽ IMPOWER(ĄfPC) @@@@@@@@@@ |
| @y1007z@ @@@@@@@ťęźęA`abơéĆŤAÚ`baĚ即đßéB |
||||||||||||||||||||||||||||||||||||
| @č @@@@@@@@@@_`(ż)Aa(Ŕ)Ab(Á)ÉÎľÄA @@@@@@@@@@ @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:B18ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC11É bnlokdw(P{rpqs(R)C|Q{rpqs(R)) đźpĹü͡éB @@@@@@@ZC12É bnlokdw(OC|P) đźpĹü͡éB @@@@@@@ZC13É bnlokdw(PC|Q) đźpĹü͡éB @@@@@@@ZC15É hlrta(bPPCbPR) đźpĹü͡éB @@@@@@@ZC16É hlrta(bPQCbPR) đźpĹü͡éB @@@@@@@ZC18ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZD18É @@@@@@ @@cdfqddr(hl`qftldms(hlchu(bPUCbPT))) @@@@@@@đźpĹü͡éB @@@l@ @@@@@@@ @@@@@@@Ŕ|Á||(P|Q)|P{ @@@@@@@ |
| @ÚÖ@ |
| @y1101z@ |
|||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:B16ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC11É sqtmb(rpqs(T)) đźpĹü͡éB @@@@@@@ZC12É rpqs(T)|bPP đźpĹü͡éB @@@@@@@ZC14É onvdq(bPPCQ)|onvdq(bPQCQ) đźpĹü͡éB @@@@@@@ZC16É Srpqs(T)|T đźpĹü͡éB @@@ÖÉÂ˘Ä @@@@@@@onvdqÖ ĽĽĽ POWER(ŔlPC) @@@@@@@@@@ @@@@@@@sqtmbÖ ĽĽĽ TRUNC(ŔlP) @@@@@@@@@@ŔlPĚŹŞđŘčĚÄÄÔˇB @@@l@ @@@@@@@ @@@@@@@ @@@@@@@ @@@@@@mFľČł˘B @ |
| @y1102z@ |
|||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB11:B14ÉăĚ\Ěć¤Éü͡éB @@@@@@@ZC11É sqtmb(rpqs(QR)) đźpĹü͡éB @@@@@@@ZC12É rpqs(QR)|bPP đźpĹü͡éB @@@@@@@ZC14É onvdq(bPQCQ){WbPQ đźpĹü͡éB @@@ÖÉÂ˘Ä @@@@@@@onvdqÖ ĽĽĽ POWER(ŔlPC) @@@@@@@@@@ @@@@@@@sqtmbÖ ĽĽĽ TRUNC(ŔlP) @@@@@@@@@@ŔlPĚŹŞđŘčĚÄÄÔˇB @@@l@ @@@@@@@ @@@@@@@ @@@@@@@[NV[gĚ ^2{W ĚlĆęvľÄ˘éąĆđmFľČł˘B @ |
| @ÚÖ@ |
| @y1201z@new@ @ @@@@@@@@ Ş|QDWČăAQDPČşĚÍÍđŽĆŤĚÚüĚlqđĎ@ˇéB |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍA2:A62ÉăĚ\Ěć¤É0.1Ť´ÝĹü͡éB @@@@@@@ZB2É A2^3+A2^2-2*A2 đźpĹü͡éB @@@@@@@ZB2đ ZĚÍÍB3:B62ÉRs[ˇéB @@@@@@@ZC2É (3*$F$2^2+2*$F$2-2)*A2-2*$F$2^3-$F$2^2 đźpĹü͡éB @@@@@@@ZC2đ ZĚÍÍC3:C62ÉRs[ˇéB @@@@@@@ZG2É F2^3+F2^2-2*F2 đźpĹü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍA1:C62đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨mUz}i˝üjnđś¸ŘŻ¸ˇéB @@@@@@B }áđíˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚÚˇčđ|RČăRČşĹAÚˇÔuđ PɡéB @@@@@@A ˛ĚÚˇčđ|POČăPOČşĹAÚˇÔuđ PɡéB @@@@@@B ˛A˛ĆŕÉAÚˇüĚX^Cđ_üɡéB 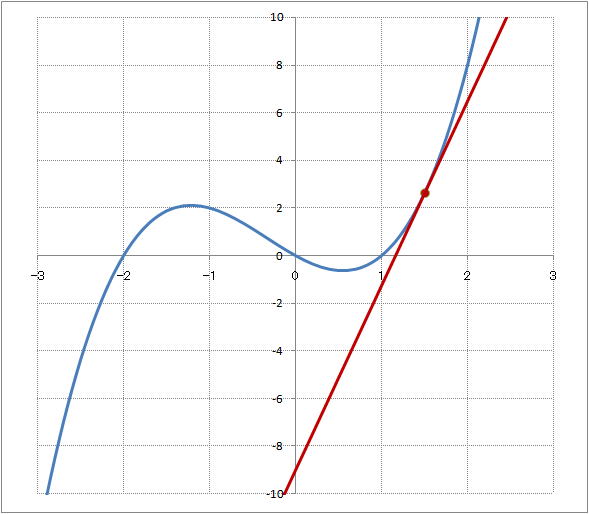 @@@}NÉÂ˘Ä @@@@@@@ @@@@@Sub Sessen() @@@@@@@@Dim t As Single @@@@@ @'P¸xŽŹ_^ĆľÄ鞡é @@@@@@@@DoEvents @@@@@@@@@@ 'ForNextJčÔľŠç§IɲŻošéć¤Éˇé @@@@@@@@For t = -2.8 To 2.1 Step 0.01 @@@@@@@@@@@Cells(2, "F") = t @@@'2sFńÉtĚlđăüˇé @@@@@@@@@@@Calculate @@@@@@@ 'ÄvZˇé @@@@@@@@Next @@@@@End Sub @@@l@ @@@@@@@}NđŔsłšÄAÚüĚŽŤđĎ@ľÄÝć¤B @@@@@@@Ú_ĚŔWŞ|QDWŠçQDPÜĹĎťˇéĆŤĚÚüĚlqŞĎ@ōܡB @ |
| @y1202z@new@ @@@@@@@@@@˛űüÉ{žŻA˝sÚŽľ˝ŕĚĹ éąĆđĎ@ˇéB |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍB3:B63ÉăĚ\Ěć¤É0.1Ť´ÝĹü͡éB @@@@@@@ZC3É $G$2*(B3-$G$3)^2+$G$4 đźpĹü͡éB @@@@@@@ZC3đ ZĚÍÍC4:C63ÉRs[ˇéB @@@@@@@ZD3É $G$2*(B3-$I$8)^2+$J$8 đźpĹü͡éB @@@@@@@ZD3đ ZĚÍÍD4:D63ÉRs[ˇéB @@@@@@@ZI7É I8 đźpĹü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍB2:D63đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨mUz}i˝üjnđś¸ŘŻ¸ˇéB @@@@@@B }áđíˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚÚˇčđ|RČăRČşĹAÚˇÔuđ PɡéB @@@@@@A ˛ĚÚˇčđ|POČăPOČşĹAÚˇÔuđ PɡéB @@@@@@B ˛A˛ĆŕÉAÚˇüĚX^Cđ_üɡéB 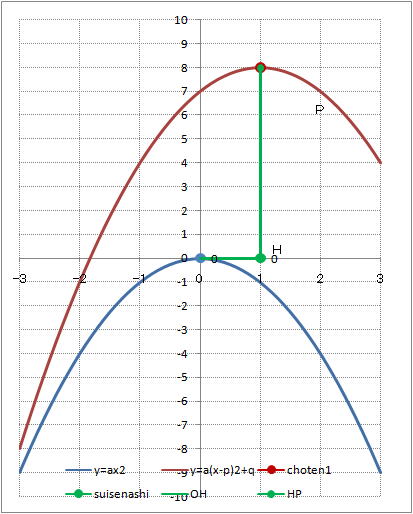 @@@@@ @@@@@
@@@}NÉÂ˘Ä @@@@@@@ @@@Option Explicit@@@@@'ĎĚéžđ§ˇé @@@Sub apq() @@@@@@@Dim a, p, q As Single@@@@@'P¸xŽŹ_^Ĺ鞡é @@@@@@@Dim sp, sq As Single@@@@@'P¸xŽŹ_^Ĺ鞡é @@@@@@@sp = Cells(8, "I")@@@@@'8sIńĚlđspÉăüˇé @@@@@@@sq = Cells(8, "J")@@@@@'8sJńĚlđsqÉăüˇé @@@@@@@Cells(3, "G") = 0@@@@@'3sGńÉ0đŤoˇ @@@@@@@Cells(4, "G") = 0@@@@@'4sGńÉ0đŤoˇ @@@@@@@DoEvents@@@@@'ForNextśŠç§IɲŻošéć¤Éˇé @@@@@@@If sp > 0 And sq > 0 Then@@@@@'ŕľA¸_ŞćPŰŔÉ éČçÎ @@@@@@@@@@Cells(3, "G") = 0@@@@@'3sGńÉ0đŤoˇ @@@@@@@@@@Cells(4, "G") = 0@@@@@'4sGńÉ0đŤoˇ @@@@@@@@@@For p = 0 To sp Step 0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'3sGńÉpĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next@p @@@@@@@@@@For q = 0 To sq Step 0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'4sGńÉqĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next@q @@@@@@@End If @@@@@@@If sp > 0 And sq < 0 Then@@@@@'ŕľA¸_Şć4ŰŔÉ éČçÎ @@@@@@@@@@Cells(3, "G") = 0@@@@@'3sGńÉ0đŤoˇ @@@@@@@@@@Cells(4, "G") = 0@@@@@'4sGńÉ0đŤoˇ @@@@@@@@@@For p = 0 To sp Step 0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'3sGńÉpĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next p @@@@@@@@@@For q = 0 To sq Step -0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'4sGńÉqĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next q @@@@@@@End If @@@@@@@If sp < 0 And sq > 0 Then@@@@@'ŕľA¸_Şć2ŰŔÉ éČçÎ @@@@@@@@@@Cells(3, "G") = 0@@@@@'3sGńÉ0đŤoˇ @@@@@@@@@@Cells(4, "G") = 0@@@@@'4sGńÉ0đŤoˇ @@@@@@@@@@For p = 0 To sp Step -0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'3sGńÉpĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next p @@@@@@@@@@For q = 0 To sq Step 0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'4sGńÉqĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next q @@@@@@@End If @@@@@@@If sp < 0 And sq < 0 Then@@@@@'ŕľA¸_Şć3ŰŔÉ éČçÎ @@@@@@@@@@Cells(3, "G") = 0@@@@@'3sGńÉ0đŤoˇ @@@@@@@@@@Cells(4, "G") = 0@@@@@'4sGńÉ0đŤoˇ @@@@@@@@@@For p = 0 To sp Step -0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'3sGńÉpĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next p @@@@@@@@@@For q = 0 To sq Step -0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'4sGńÉqĚlđŤoˇ @@@@@@@@@@@@@Calculate@@@@@'ÄvZˇé @@@@@@@@@@Next q @@@@@@@End If @@@End Sub @@@l@ @@@@@@@}NđŔsłšÄA @@@@@@É{žŻA˛űüÉ{žŻA˝sÚŽľ˝ŕĚĹ éąĆđĎ@ľÄÝć¤B @ |
| @ÚÖ@ |
| @y1301z new@}Nđp˘ÄAQOČşĚfđßéB@@@@@@@@@@@ |
@@@fÉÂ˘Ä @@@@@@@fĆÍAPĆŠŞŠgČOÉłĚńđ˝Č˘QČăĚŠR̹ƚB @@@@@@@Ě}NĹÍAQČăAŠŞŠgćčPŹł˘ÜĹAęÂęÂčZđľÄčŘęéŠ @@@@@@˛×éąĆÉćÁÄfĹ éŠŰŠđťfľÄ˘ÜˇBęÂĹŕčŘę˝ČçÎfĹÍ @@@@@@ȢąĆÉČčܡB @@@}NÉÂ˘Ä @@@@@@@ @@@Sub Sosu2() @@@@@@For n = 2 To 20 @@@@@@@@@d = 0 @@@@@'dđúťˇé @@@@@@@@@For k = 2 To n - 1 @@@@@@@@@@@@If n Mod k = 0 Then @@@@@'kŞnĚńČçÎ @@@@@@@@@@@@@@@d = d + 1@@@@@ 'dÉPđÁŚé @@@@@@@@@@@@End If @@@@@@@@@Next k @@@@@@@@@If d = 0 Then @@@@@'d=0ČçÎ @@@@@@@@@@@@MsgBox (n & "ÍfšI") @@@@@'nÍfƢ¤bZ[Wđ\Śˇé @@@@@@@@@End If @@@@@@Next n @@@@@@MsgBox ((n - 1) & " ČşĚfĚTőđIšľÜľ˝B") @'uIšvĚbZ[Wđ\Śˇé @@@End Sub @@@l@ @@@@@@@}NđŔsłšÄAQOČşĚfđßÄÝć¤B @@@@@@@ÉA}N𫷦ÄAROČşĚfđßÄÝć¤B @ |
| @y1302z@new@˝čĹÍȢű@ĹAŽSđßéB@ | ||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@@@@@Ś ĚčÉ]ÁÄADńđ uĽĽĽĽĽE-12vƢ¤\ŚĹÍȢć¤ÉľÄ¨B @@@@@@@@@DńđIđ ¨ ENbN ¨ ZĚŽÝč ¨ \Ś`Ž ¨ l ¨ nj @@@ŽSÉÂ˘Ä @@@@@@@ŽSĆÍAŠŞŠg𢽳ĚńĚaŞŠŞŠgĆľČéŠR̹ƚB @@@@@@@áŚÎAUĚńÍAŠŞŠgđĆAPĆQĆRĹ čAP{Q{RU ÉČéĚĹAUÍ @@@@@ ŽSšB @@@@@@ŞQČăĚŠRĹA@ @@@@@iäńĚaĚöŽđp˘ÄČPÉŘžˇéąĆŞĹŤÜˇBj @@@@@@ťęĹÍSÄĚŽSÍA @@@@@@ôĚSÄĚŽSÍA @@@@@˘ÜˇB @@@@@@ľŠľAďĚŽS͢žŠłęĢܚńBďĚŽSŞśÝľČ˘ąĆÍŘžłęÄ @@@@@˘Č˘ĚšB @@@@@@ČşĚ}NĹÍAw ŞQČăĚŠRĹA@ @@@@ ŽSÉČé xąĆđpľÄAŽSđßĢܡB @@@}NÉÂ˘Ä @@@Sub Kanzensusp() @@@@@@Dim n As Long @@@@@'ˇŽ^Ĺ鞡é @@@@@@Dim k As Long @@@@@'ˇŽ^Ĺ鞡é @@@@@@Dim d As Long @@@@@'ˇŽ^Ĺ鞡é @@@@@@'Cells.Clear @@@@@@DoEvents @@@@@'For[vĚrĹŕâ~ĹŤéć¤Éˇé @@@@@@For n = 2 To 31 @@@@@@@@@Cells(n, "A") = n @@@'ns`ńÉnĚlđăüˇé @@@@@@@@@Cells(n, "B") = 2 ^ n - 1@@@ 'nsBńÉ2 ^ n - 1Ělđăüˇé @@@@@@@@@d = 0@@@@@ 'dđúťˇé @@@@@@@@@For k = 2 To 2 ^ n - 1 - 1 @@@@@@@@@@@@If (2 ^ n - 1) Mod k = 0 Then @@@'ŕľAkŞ 2 ^ n - 1 ĚńČçÎA @@@@@@@@@@@@@@@d = d + 1@@@ 'dÉPđÁŚé @@@@@@@@@@@@End If @@@@@@@@@Next k @@@@@@@@@If d = 0 Then @@@@@'ŕľAd=0 ČçÎ @@@@@@@@@@@@Cells(n, "C") = "f" @@@'nsCńÉ"f"đăüˇé @@@@@@@@@End If @@@@@@@@@Cells(n, "D") = (2 ^ (n - 1)) * (2 ^ n - 1) 'nsDńÉ(2 ^ (n - 1)) * (2 ^ n - 1) Ělđăü @@@@@@@@@If Cells(n, "C") = "f" Then @@@@@'ŕľAnsCńŞ"f"ČçÎA @@@@@@@@@@@@Cells(n, "E") = "ŽS" @@@@@'nsEńÉ"ŽS"đăüˇé @@@@@@@@@End If @@@@@@Next n @@@@@@MsgBox ("ŽSĚTőđIšľÜľ˝...") 'uIšvĚbZ[Wđ\Śˇé @@@End Sub @@@l@ @@@@@@@}NđŔsłšÄAŽSđßÄÝć¤B @@@@@@WÂÚĚŽSŞÜéÜŽԪŠŠčܡB @ |
| @ÚÖ@ |
| @y1401z@new@ÉűöŽ ĆĚ\ˇ}`iłtČüjđ`B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍA2:A362ÉăĚ\Ěć¤ÉPŤ´ÝĹü͡éB @@@@@@@ZB2É SIN($F$2*RADIANS(A2)) đźpĹü͡éB @@@@@@@ZB2đ ZĚÍÍB3:B362ÉRs[ˇéB @@@@@@ ZC2É B2*COS(RADIANS(A2)) đźpĹü͡éB @@@@@@@ZC2đ ZĚÍÍC3:C362ÉRs[ˇéB @@@@@@ ZD2É B2*SIN(RADIANS(A2)) đźpĹü͡éB @@@@@@@ZD2đ ZĚÍÍD3:D362ÉRs[ˇéB @@@@@@@ZE2É ua=vđü͡éB @@@@@@@ZF2É u2vđ đü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍC2:D362đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨mUz}i˝üjnđś¸ŘŻ¸ˇéB @@@@@@B }áđíˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚÚˇčđ|PČăPČşĹAÚˇÔuđ ODPɡéB @@@@@@A ˛ĚÚˇčđ|PČăPČşĹAÚˇÔuđ ODPɡéB @@@@@@B ˛A˛ĆŕÉAÚˇüĚX^Cđ_üɡéB 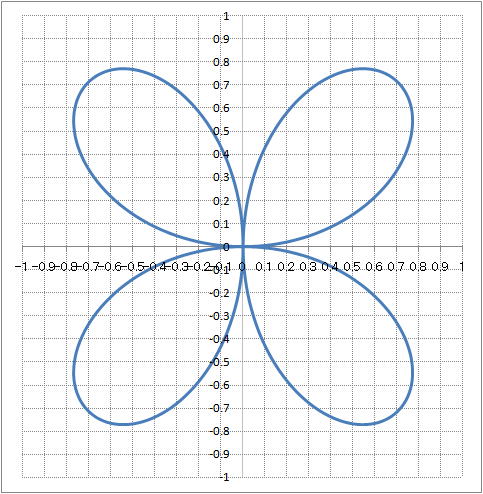 @@@@@@@q`ch`mrÖ ĽĽĽ q`ch`mr(x@Ěpx) @@@@@@@@@@x@ĚpxđĘx@iWAjÉϡˇé @@@}NÉÂ˘Ä @@@@@@@Sub Seiyou() @@@@@@@@@@Dim a As Single@@@'ađP¸xŽŹ_^Ĺ鞡é @@@@@@@@@@For a = 0 To 10.05 Step 0.05 @@@@@@@@@@@@@Cells(2, "F") = a@@@'2sFńÉĚlđăüˇé @@@@@@@@@@@@@Calculate@@@'ÄvZˇé @@@@@@@@@@Next a @@@@@@@End Sub @@@l@ @@@@@@@ZF2iĚljÉA2A3A4AEEEA10 đăüľÄA`Šęé}`iłtČüjđĎ@ľ @@@@@ ÄÝć¤B @@@@@@@Ü˝A}NđŔsłšÄAĚlŞOŠçPOÜĹAODOTŤ´ÝĹĎťˇéĆŤÉ`Šęé @@@@@}`đĎ@ľÄÝć¤B @ |
| @y1402z@new@ÉűöŽ ĆĚ\ˇ}`iALfXĚQŞŤüjđ`B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @č @@@(1) ČşĚÎ\đ[NV[gÉ쏡éB
@@@Ql @@@@@săĚ[NV[gĚüÍű@t @@@@@@@ZĚÍÍA2:A722ÉăĚ\Ěć¤ÉPŤ´ÝĹü͡éB @@@@@@@ZB2É $F$2*RADIANS(A2) đźpĹü͡éB @@@@@@@ZB2đ ZĚÍÍB3:B722ÉRs[ˇéB @@@@@@ ZC2É B2*COS(RADIANS(A2)) đźpĹü͡éB @@@@@@@ZC2đ ZĚÍÍC3:C722ÉRs[ˇéB @@@@@@ ZD2É B2*SIN(RADIANS(A2)) đźpĹü͡éB @@@@@@@ZD2đ ZĚÍÍD3:D722ÉRs[ˇéB @@@@@@@ZE2É ua=vđü͡éB @@@@@@@ZF2É u2vđ đü͡éB @@@(2) ăL(1)ĚÎ\ŠçOtđ`B @@@@@@@ ăL(1)ĚÎ\ĚZĚÍÍC2:D722đhbOľÄIđˇéB @@@@@@A m}ün¨mUz}n¨mUz}i˝üjnđś¸ŘŻ¸ˇéB @@@@@@B }áđíˇéB @@@(3) OtĚ`ŠęĢéŔW˝ĘđŽŚéB @@@@@@@ ˛ĚÚˇčđ|PTOČăPTOČşĹAÚˇÔuđ ROɡéB @@@@@@A ˛ĚÚˇčđ|PTOČăPTOČşĹAÚˇÔuđ ROɡéB @@@@@@B ˛A˛ĆŕÉAÚˇüĚX^Cđ_üɡéB 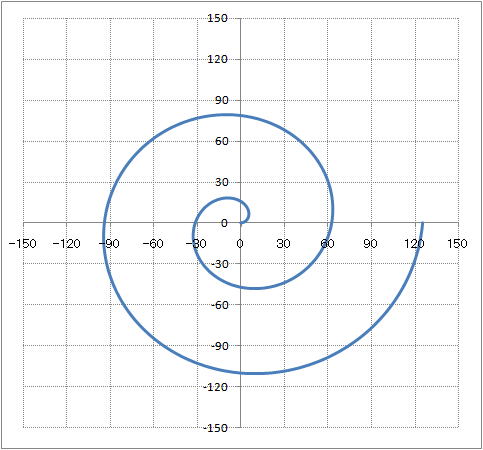 @@@ÖÉÂ˘Ä @@@@@@@q`ch`mrÖ ĽĽĽ q`ch`mr(x@Ěpx) @@@@@@@@@@x@ĚpxđĘx@iWAjÉϡˇé @@@}NÉÂ˘Ä @@@@@@@Sub Aruki() @@@@@@@@@@Dim a As Single@@@'@@@'ađP¸xŽŹ_^Ĺ鞡é @@@@@@@@@@For a = 0 To 10.05 Step 0.05 @@@@@@@@@@@@@Cells(2, "F") = a@@@''2sFńÉĚlđăüˇé @@@@@@@@@@@@@Calculate@@@'ÄvZˇé @@@@@@@@@@Next a @@@@@@@End Sub @@@l@ @@@@@@@ZF2iĚljÉA2A3A4AEEEA10 đăüľÄA`Šęé}`iALfXĚQŞ @@@@@@ŤüjđĎ@ľÄÝć¤B @@@@@@@Ü˝A}NđŔsłšÄAĚlŞOŠçPOÜĹAODOTŤ´ÝĹĎťˇéĆŤÉ`Šęé @@@@@}`đĎ@ľÄÝć¤B @ |
| Ś@ăLĚTvf[^t@Cu`DvđČşĹ_E[hōܡB |
| @ÚÖ@ |
| @şĚwd
x Ěg˘űđlŚéTvf[^ đ_E[hˇéĆA łk()t@Cusample_excel.lzhvŞ_E[hłęéB @_E[hłę˝łk()t@Cusample_excel.lzhvđđˇéĆA tH_ uwd x Ěg˘űđlŚéTvf[^vŞěŹłęéB @şĚuV~ [VvufĆŽSvuÉűöŽv Tvf[^ đ_E[hˇéĆA łk()t@CuExcelSample2.lzhvŞ_E[hłęéB @_E[hłę˝łk()t@CuExcelSample2.lzhvđđˇéĆA tH_ uuV~ [VvufĆŽSvuÉűöŽv Tvf[^vŞěŹłęéB |
| @d Tvf[^ | @wd x Ěg˘űđlŚéTvf[^ |
| @d Tvf[^Q@ | @uV~ [VvufĆŽSvuÉűöŽvTvf[^ |
| @ÚÖ@ |
| @tH_ uwd x Ěg˘űđlŚéTvf[^v ĚÉÍAPPÂĚtH_uy0100zQÖvAuy0200zOpÖvAuy0300zwÖvAuy0400zÎÖvAuy0500z˘ë˘ëČČüvAuy0600z÷Ş(ťĚP)vAuy0700z÷Ş(ťĚQ)vAuy0800zĎŞvAuy0900zńvAuy1000zĄfvAuy1100z˝űŞĚpvŞ éBetH_ĚĚt@Cu`Dvđ d ĹJiÇÝŢjB |
| @tH_ uuV~
[VvufĆŽSvuÉűöŽvTvf[^v ĚÉÍAUÂĚt@CŞ éB @et@Cu`Dmvđ d ĹJiÇÝŢjB |