 |

 |

| LastUpdate 11/29/2024 |
| @"Grapes" and "Function View" are famous as excellent free software that draws very easily just by substituting formulas of functions. @In high school mathematics classes , when teaching graphs of quadratic functions , students create an xy correspondence table , plot the points on the xy-coordinate plane , and draw a graph by connecting the points with a smooth curve. @"Grapes" and "Function View"draw graphs simply by substituting function expressions.@Therefore , there is little sense of creating an xy correspondence table , plotting the points , and connecting them with a smooth curve. @However , Excel is the software that makes it possible on a computer to create an xy correspondence table , plot points , and draw a graph with a sense of connecting them with a smooth curve. Excel is a spreadsheet sofrware that we use on a daily basis. @When I went to a public library in Higashi-Omi , I happened to come across a book titled "Easy Mathematics Learning with Excel (from Trigonometory to Calculus) , Co-authered by Yukihisa Takahashi and Ha Watanabe , Ohmusha Publishinng". I found a description that made me realize that how to draw a graph of a funcion using "Excel" and the way of thinking about numerical sequences is exactly the copy function of "Excel". @In addition , I introduced what can be done using "Excel" in "Simulation" , "Prime and Perfect Numbers" , and "Polor Equations" in Table of Contents 12-14. Please try it. You should be able to apply it to the other things as well. @By using "Grapes" , "Function View" , and "Excel" according to the senses , skills , and knowledge you want students to acqure , I believe that more effective lessons can be organized. |
| http://kn-makkun.com/MakkunWp/excels.html |
| No | Table of contents |
| P | @Quadatic function |
| Q | @Trigonometric function |
| R | @Exponential function |
| S | @Logarithmic function |
| T | @Varius curves |
| U | @Differentiation (Part 1) |
| V | @Differentiation (Part 2) |
| W | @Integral |
| X | @Number sequence |
| PO | @Complex number |
| PP | @Application of square root |
| PQ | @Simulation @ |
| PR | @Prime snd perfect numbers@ |
| PS | @Polar equation@ |
| PT | @Download@ |
| PU | @How to use the sample data |
| Back to the Top Page |
| @To table of contents@ |
| @yPOPz Draw a graph of the quadratic functions of y=x^2 , y=2x^2 , and y=3x^2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -4 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B20 , right-click , and select Paste. @@@@@@@Enter =B12^2 in half-width in cell C12. @@@@@@@Enter =2*B12^2 in half-width in cell D12. @@@@@@@Enter =3*B12^2 in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C20 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E20 in the correspondence table of (1) above. @@@@@@A Left-click [Insert]¨[Scatter plot]¨[Smooth line and marker]. @@@(3) Arrange the xy coordinate plane on which the graoh is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add grid lines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 5.0 @@@@@@¨ Close @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click [Insert]¨[Scatter plot]¨[Smooth line]. @@@@@@ 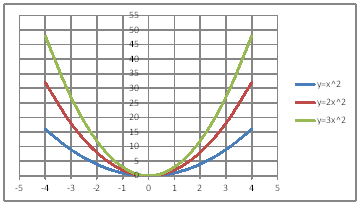 @@@Consideration 1 @@@@@@Compare the spread of graphs of y=x^2 , y=2x^2 , and y=3x^2.@ @@@Consideration 2 @@@@@@In general , how does the spread of the graph of y=ax^2 change depending on the value of a ? |
| @yPOQz Draw a graph of the quadratic functions of y=2x^2 and y=-2x^2. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to yPOPz how to enter the worksheet.
@@@ (2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correspondence table of (1) above. @@@@@@A Left click mInsertn¨mScatter plotn¨mSmooth line and Markern @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 5.0 @@@@@@¨ Close @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it . @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@ @@@@@@ 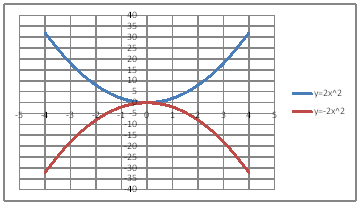 @@@@@@ @@@Consideration 1 @@@@@@State the positional relationship between the graphs of y=2x^2 and y=-2x^2.@ @@@Consideration 2 @@@@@@In general , what is the positional relationship between the graphs of y=ax^2 and y=-ax^2 ? |
| @yPORz Draw a graph of the quadratic functions of y=2x^Q , y=2x^2+3 , and y=2x^2-3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to yPOPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E20 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Markern. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 5.0 @@@@@@¨ Close @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph-area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line] @@@@@@ 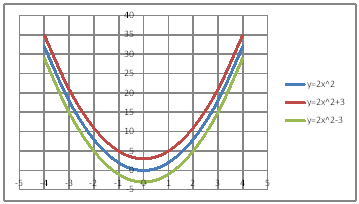 @@@Consideration 1 @@@@@@@Compare the spread of the graphs of y=2x^2 , y=2x^2+3 , and y=2x^2-3. @@@Consideration 2 @@@@@@@State the positional relationship of the graphs of y=2x^2 , y=2x^2+3 , and y=2x^2-3. @@@Consideration 3 @@@@@@@In general , what is the positional relationship between graphs of y=ax^2 and y=ax^2+b ? |
| @yPOSz Draw a graph of the quadratic functions of y=2x^2 , y=2(x+2)^2 , and y=2(x-2)^2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to yPOPz how to enter the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E20 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Markern @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 5.0 @@@@@@¨ Close @@@(4) Deleate points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@ 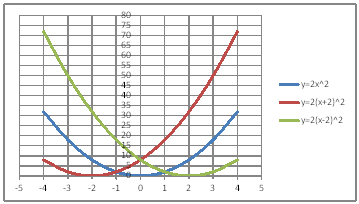 @@@Consideration 1 @@@@@@@Compare the spread of the graphs of y=2x^2 , y=2(x+2)^2 , and y=2(x-2)^2. @@@Consideration 2 @@@@@@@State the positional relationship of the graphs of y=2x^2 , y=2(x+2)^2 , and y=2(x-2)^2. @@@Consideration 3 @@@@@@@In general , what is the positional relationship between graphs of y=ax^2 and y=a(x-b)^2 ? |
| @yPOTz Draw a graph of the quadratic functions of y=2x^2 and y=2(x-2)^2+3. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the folllowing correspondence table on the worksheet. @@@Reference @@@@@@Please refer to yPOPz how to enter the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correspondence table of (1) above. @@@@@@A Left -click mInsertn¨mScatter plotn¨mSmooth line and Marker]. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@ 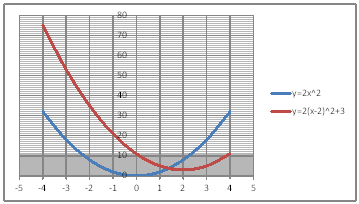 @@@Consideration 1 @@@@@@@Compare the spread of the graphs of y=2x^2 and y=2(x-2)^2+3. @@@Consideration 2 @@@@@@@State the positional relationship of the graphs of y=2x^2 and y=2(x-2)^2+3. @@@Consideration 3 @@@@@@@In general , what is the positional relationship between the graphs of y=ax^2 and y=a(x-b)^2+c. |
| @yPOUz Draw a graph of the quadratic functions of y=-x^2 and y=-x^2+6x-7. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to @yPOPz how to enter the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Markern @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@ 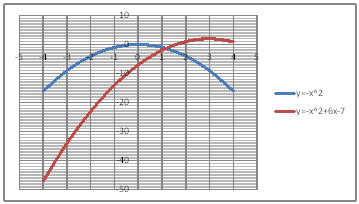 @@@Consideration 1 @@@@@@@Compare the spread of the graphs of y=-x^2 and y=-x^2+6x-7. @@@Consideration 2 @@@@@@@State the positional relationship of the graphs of y=-x^2 and y=-x^2+6x-7. |
| @To table of contents@ |
| @yQOPz Draw a graph of the trigonometric functions of , Q , and R. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and select Paste. @@@@@@@Enter = SIN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter = SIN(RADIANS(2*B12)) in half-width in cell D12 @@@@@@@Enter = SIN(RADIANS(3*B12)) in half-width in cell E12 @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 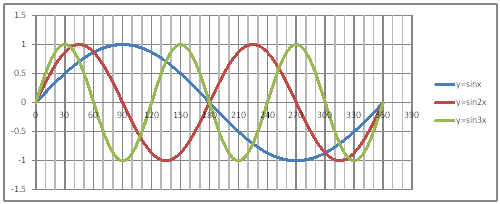 @@@Consideration 1 @@@@@@@@Find the period of the graph of from the graph. @@@Consideration 2 @@@@@@@@Find the period of the graph of 2x from the graph. @@@Consideration 3 @@@@@@@@Find the period of the graph of R from the graph.@ @@@Consideration 4 @@@@@@@@In general , what can be said about the period of the graph of y=sinax ? |
| yQOQz Draw graphs of the trigonometric functions y=sinx and y=sin(x/2). | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B372 , right-click , and select Paste. @@@@@@@Enter =SIN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =SIN(RADIANS(B12/2)) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:D372 , right-click , and select Paste @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D372 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 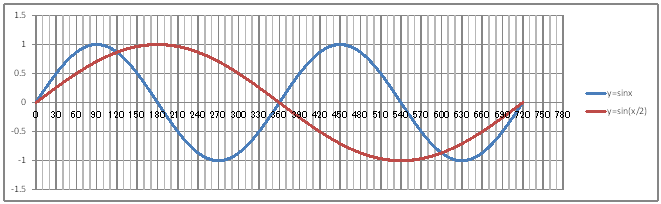 @@@Consideration 1 @@@@@@@Find the period of the graph of y=sin(x/2) from the graph ? @@@Consideration 2 @@@@@@@In general , @@@@@@@what can be said about the period of the graph of y=sin(x/a) ? @ |
| @yQORz Draw a graph of the trigonometric functions of y=sinx , y= 2sinx , and y=3sinx ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and elect Paste. @@@@@@@Enter =SIN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =2*SIN(RADIANS(B12)) in half-width in cell D12. @@@@@@@Enter =3*SIN(RADIANS(B12)) in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and elect Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 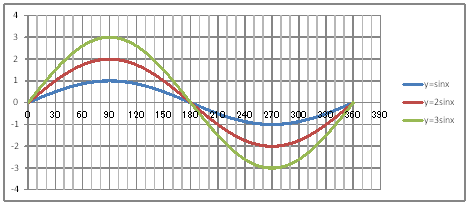 @@@Consideration 1 @@@@@@@@Find the period of the graph of y=2sinx from the graph. @@@Consideration 2 @@@@@@@@Find the period of the graph of y=3sinx from the graph. @@@Consideration 3 @@@@@@@@State the difference between graphs y=sinx , y=2sinx , and y=3sinx. @@@Consideration 4 @@@@@@@@In general , what can be said about the amplitude of the graph of y=asinx ? |
| @yQOSz Draw a graph of the trigonometric function y=2sin(x-60). | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet above.t @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B222 , right-click , and select Paste. @@@@@@@Enter =2*SIN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =2*SIN(RADIANS(B12-60)) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C222 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D222 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 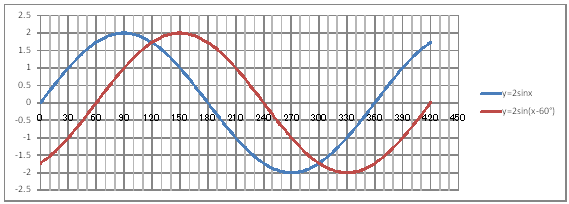 @@@Consideration @@@@@@@Make sure that y=2sin(x-60) graph is the y=2sinx graph translated +60 along the x-axis. |
| @yQOTz Draw a graph of the trigonometric functions y=cosx , y=cos2x , and y=cos3x. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and select Paste. @@@@@@@Enter =COS(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =COS(RADIANS(2*B12)) in half-width in cell D12. @@@@@@@Enter =COS(RADIANS(3*B12)) in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E192 in the correspondence table of (1) above @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area by horizontally by dragging the right and lrft edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 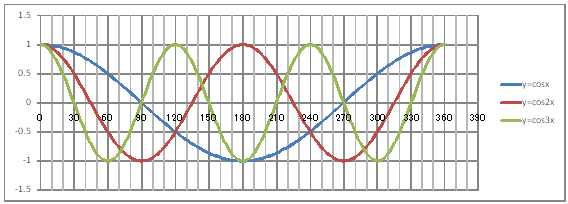 @@@Consideration 1 @@@@@@@@Find the period of the graph of y=cosx from the graph. @@@Consideration 2 @@@@@@@@Find the period of the graph of y=cos2x from the graph. @@@Consideration 3 @@@@@@@@Find the period of the graph of y=cos3x from the graph. @@@Consideration 4 @@@@@@@@In general , what can be said about the period of the graph of y=cosax ? |
| @yQOUz Draw a graph of the trigonometric functions y=cosx and y=cos(x/2). | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Procedure @@@@@sHow to complete the worksheet above.t @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B372 , right-click and select Paste. @@@@@@@Enter =COS(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =COS(RADIANS(B12/2)) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click and select Copy. @@@@@@@Drag the cell range C13:C372 , right-click and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D372 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 30.00 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale intercal Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 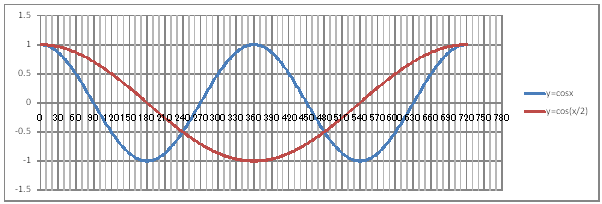 @@@Consideration 1 @@@@@@@Find the period of the graph of y=cos(x/2) . @@@Consideration 2 @@@@@@@In general, @@@@@@@what can be said about the period of the graph of y=cos(x/a) ? |
| @yQOVz Draw a graph of the trigonometric functions y=cosx , y=2cosx , and y=3cosx. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet above.t @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 , right-click , and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and select Paste. @@@@@@@Enter =COS(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =2*COS(RADIANS(B12)) in half-width in cell D12. @@@@@@@Enter =3*COS(RADIANS(B12)) in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliay gridlines @@@@@@ 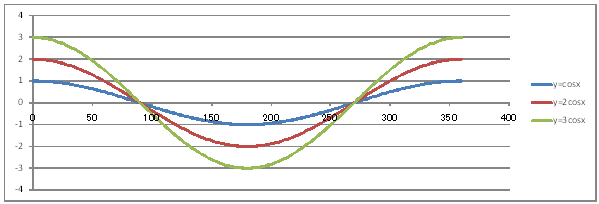 @@@Consideration 1 @@@@@@@@Find the period of the graph of y=2cosx from the graph. @@@Consideration 2 @@@@@@@@Find the period of the graph of y=3cosx from the graph @@@Consideration 3 @@@@@@@@State the difference between graph , graph Q , and graph R. @@@Consideration 4 @@@@@@@@In general , what can be said about the amplitude of the graph of ? |
| @yQOWz Draw a graph of the trigonometric function y=2cos(x+60). | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -60 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B222 , right-click , and select Paste. @@@@@@@Enter =2*cos(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =2*cos(RADIANS(B12+60)) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12, right-click , and select Copy. @@@@@@@Drag the cell range C13:C222 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D222 on the correspondence table of (1) above. @@@@@@A Left -click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 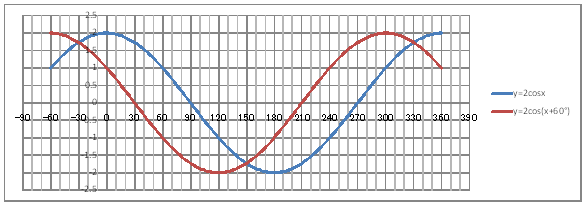 @@@Consideration @@@@@@@Make sure that the graph of y=2cos(x+60) @is the graph of y=2cosx that has been translated by -60 in the x-axis direction. |
| @yQOXz Draw a graph of the trigonometric function y=tanx. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -180 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B56 , right-click , and select Paste. @@@@@@@Enter -88 in half-width in cell B58. @@@@@@@Enter =B58+2 in half-width in cell B59. @@@@@@@Right-click cell B59 and select Copy. @@@@@@@Drag the cell range B60:B146 , right-click , and select Paste. @@@@@@@Enter 92 in half-width in cell B148. @@@@@@@Enter =B148+2 in half-width in cell B149. @@@@@@@Right-click cell B149 and select Copy. @@@@@@@Drag the cell range B150:B192 , right-click , and select Paste. @@@@@@@Enter =TAN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Right-click cell C12 and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) avobe. @@@@@@@ Drag and select the cell range B11:C192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 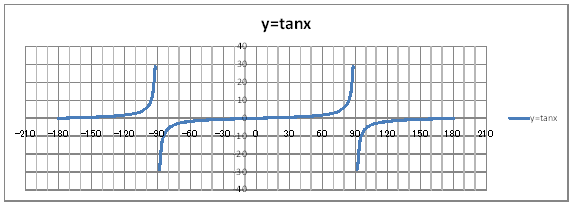 @@@Consideration 1 @@@@@@@@Find the period of the graph of y=tanx from the graph. @@@Consideration 2 @@@@@@@@Make sure that the straight lines x=90and x=-90are asymptote.@ |
| @yQPOz Draw a graph of the trigonometric function of y=tan2x. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@Reference @@@@@sHow to complete the woksheet abovet @@@@@@@Enter -90in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click cell B13 and select Copy. @@@@@@@Drag the cell range B14:B56 , right-click , and select Paste. @@@@@@@Enter -44 in half-width in cell B58. @@@@@@@Enter =B58+1 in half-width in cell B59. @@@@@@@Right-click cell B59 and select Copy. @@@@@@@Drag the cell range B60:B146 , right-click , and select Paste. @@@@@@@Enter 46 in half-width in cell B148. @@@@@@@Enter =B148+1 in half-width in cell B149. @@@@@@@Right-click cell B149 and select Copy. @@@@@@@Drag the cell range B150:B192 , right-click , and select Paste. @@@@@@@Enter =TAN(RADIANS(2*B12)) in half-width in cell C12. @@@@@@@Right-click cell C12 and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C192 in the correspnndencetable of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval 15.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval 5.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 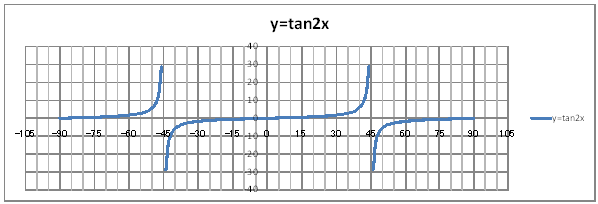 @@@Consideration 1 @@@@@@@@Find the period of the graph of y=tan2x from the graph.@ @@@Consideration 2 @@@@@@@@Make sure that the straight lines x=45and x=-45are asymptote. @@@Consideration 3 @@@@@@@@In general , what can be said about the period of th graph of y=tanax ? |
| @yQPPz Draw a graph of the trigonometric functions y=tanx and y=2tanx. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@@@@@Reference @@@@@@@@@@Please refer to yQOXz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cellrange B11:D192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area vertically and horizontally by dragging the top and bottom edges and the @@@@@@@right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the number on the x-axis ¨ Axis formating ¨ Scale interval Fixed 15.0 @@@@@@¨ Close ¨ Right-click on the number on the x-axis ¨ Add gridlines @@@@@@A Right-click on the number on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 5.0 @@@@@@¨ Close ¨ Right-click on the number on the x-axis ¨ Add auxiliary gridlines @@@@@ B Right-click on the number on the y-axis ¨ Axis-formating ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the number on the y-axis ¨ Add auxiliary gridlines @@@@@@ 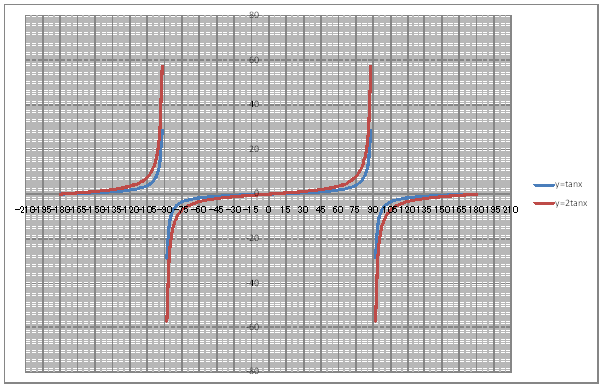 @@@Consideration 1 @@@@@@@@Find the period of the graph of y=2tanx from the graph. @@@Consideration 2 @@@@@@@@State the positional relationship between the graphs of and Q. @@@Consideration 3 @@@@@@@@In general , what is the positional relationship between the graphs of and . |
| @yQPQz Draw a graph of the trigonometric function y=2tan{(1/2))x-30}. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@@@@@Reference @@@@@@@@@@Please refer to yQOXz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C372 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linesn. @@@@@@B Expand the graph area vertically and horizontally by dragging the right and reft edges and the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 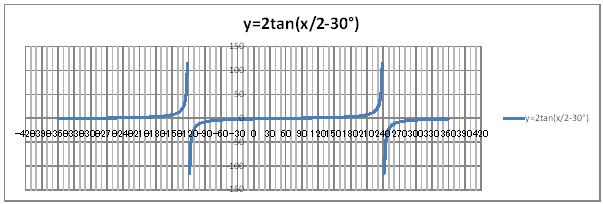 @@@Consideration 1 @@@@@@@Make sure that the straight lines x=240 and x=-120 are asymptote of the graph@of y=2tan{(1/2)x-30} @@@Consideration 2 @@@@@@@Make sure that the graph of y=2tan(1/2)x is translated by +60 in the x-axis direction. |
| @yQPRz When 0
360 @@@@@@Draw a graph of the functions y=cos2x+2sinx+2 and y=-2(sinx)^2+2sinx+3. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and select Paste. @@@@@@@Enter 0 in half-width in cell D12. @@@@@@@Enter =D12+2 in half-width in cell D13. @@@@@@@Right-click on cell D13 and select Copy. @@@@@@@Drag the cell range D14:D192 , right-click , and select Paste. @@@@@@@Enter =COS(RADIANS(2*B12))+2*SIN(RADIANS(B12))+2@in half-width in cell C12. @@@@@@@Enter =-2SIN(RADIANS(B12))^2+2*SIN(RADIANS(B12))+3@in half-width in cell E12. @@@@@@@Right-click on cell D12 and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@@@@@Right-click on cell E12 and select Copy. @@@@@@@Drag the cell range E13:E192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) avove. @@@@@@@ Drag and select the cell range B11:C192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨msmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@@@@C Drag and select the cell range D11:E192 in the correspondence table of (1) above. @@@@@@D Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@E Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 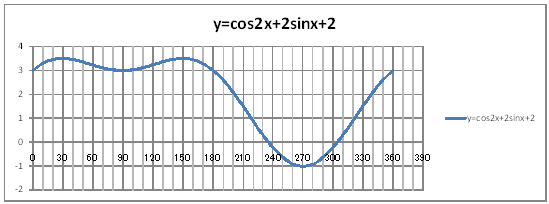 @@@@@@ 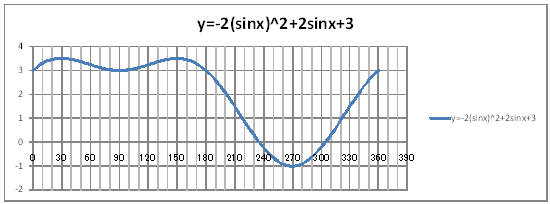 @@@l@ @@@@@@@Make sure that the graphs for y=cos2x+2sinx+2 and y=-2(sinx)^2+2sinx+3 are the same. |
| @yQPSz When 0
360 @@@@@@Draw a graph of the functions of y=sinx+cosx and y=ã2sin(x+45). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence tabe on the worksheet.
@@@ReferencesHow to complete the worksheet abovet @@@@@@Enter 0 in half-width in cell B12. @@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@Right-click cell B13 amd select Copy. @@@@@@Drag the cell range B14:B192 , Right-click , and select Paste. @@@@@@Enter 0 in half-width in cell D12. @@@@@@Enter =D12+2 in half-width in cell D13. @@@@@@Right-click cell D13 amd select Copy. @@@@@@Drag the cell range D14:D192 , Right-click , and select Paste. @@@@@@Enter =SIN(RADIANS(B12))+COS(RADIANS(B12)) in half-width in cell C12. @@@@@@Enter =SQRT(2)*SIN(RADIANS(B12+45)) in half-width in cell E12. @@@@@@Right-click cell C12 amd select Copy. @@@@@@Drag the cell range C13:C192 , Right-click , and select Paste. @@@@@@Right-click cell E12 amd select Copy. @@@@@@Drag the cell range E13:E192 , Right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C192 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@@@@C Drag and select the cell range D11:E192 in the correspondence table of (1) above. @@@@@@D Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@E Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 30.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 10.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@ 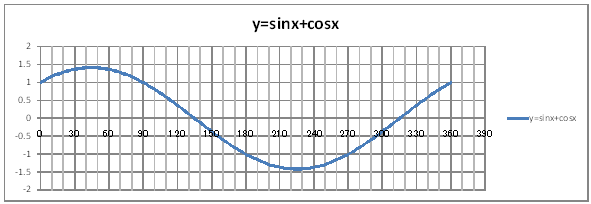 @@@@@@ 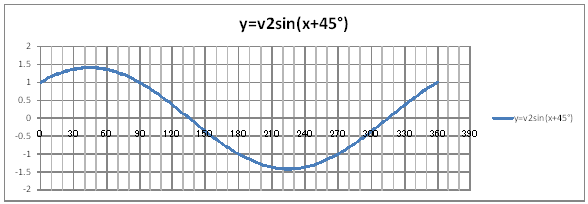 @@@Consideration @@@@@@@Make sure that the gtaphs for { and y=ã2sin(x+45)@are the same. |
| @To table of contents@ |
| @yROPz Draw a graph of the exponential functions of y=2^x , y=3^x , and y=4^x. | |||||||||||||||||||||||||||||||||||
| @ @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -2 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click B13 and select Copy. @@@@@@@Drag the cell range B14:B16, right-click , and select Paste. @@@@@@@Enter =POWER(2,B12) in half-width in cell C12. @@@@@@@Enter =POWER(3,B12) in half-width in cell D12. @@@@@@@Enter =POWER(4,B12) in half-width in cell E12. @@@@@@@Drag the cell range C12:E12, right-click , and select Copy @@@@@@@Drag the cell range C13:C16 , right-click , and select Paste @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E16 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth lines and Marker] @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ Close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete the points(markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@ 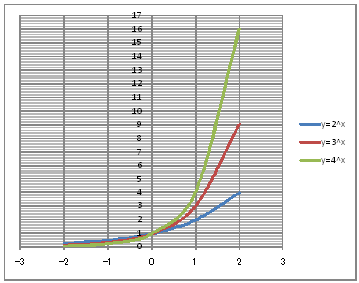 @@@Consideration 1 @@@@@@@Find the coordinates of the point through which the graphs of y=2^x , y=3^x , and y=4^x commonly pass. @@@Consideration 2 @@@@@@@Find the asymptote that the graphs of y=2^x , y=3^x , and y=4^x have in common. @@@Consideration 3 @@@@@@@State the difference between graphs y=2^x , y=3^x , and y=4^x. |
| @yROQz Draw a graph of the exponential functions of y=(1/2)^x , y=(1/3)^x , and y=(1/4)^x. | |||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Refer to yROPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E16 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Markern. @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ Close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delite the points(markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen. @@@@@@ 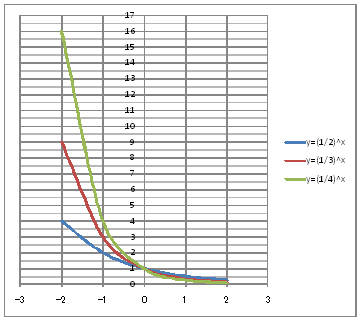 @@@Consideration 1 @@@@@@@Find the coordinates of the point through which the graphs of y=(1/2)^x , y=(1/3)^x , and y=(1/4)^x commonly pass. @@@Consideration 2 @@@@@@@Find the asymptote that the graphs of y=(1/2)^x , y=(1/3)^x , and y=(1/4)^x have in common. @@@Consideration 3 @@@@@@@State the difference between the graphs y=(1/2)^x , y=(1/3)^x , and y=(1/4)^x. |
| @yRORz Draw a graph of the exponential functions of y=2^x and y=(1/2)^x . | ||||||||||||||||||||||||||||||||||||
@Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to yROPz how to complete the worksheet
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D18 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line snd markern. @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ Close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete the points(markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen. @@@@@@ 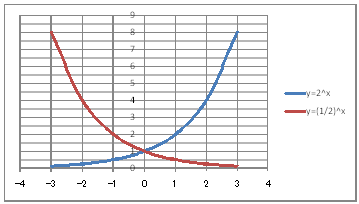 @@@Consideration 1 @@@@@@@State the positional relationship of the graphs of y=2^x and y=(1/2)^x. @@@Consideration 2 @@@@@@@In general , what is the positional relationship between graphs y=a^x and y=(1/a)^x ? |
| @yROSz Draw a graph of the exponential functions of y=2^x , y=2^(x-2) , and y=2^(x+2). | |||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@Please refer to yROPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E18 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Markern. @@@@@@B Expand the graph area horizontally by dragging the right and left edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formating ¨ Scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formating ¨ Scale interval Fixed 5.0 @@@@@@¨ Close @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formating ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ Close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete the points(markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen. @@@@@@ 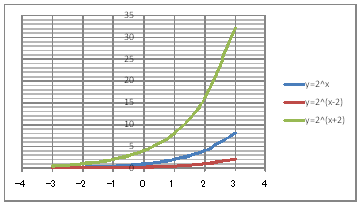 @@@Consideration 1 @@@@@@@State the positional relationship of the graph of y=2^x , y=2^(x-2) , and y=2^(x+2). @@@Consideration 2 @@@@@@@In general , what is the positional relationship between graphs y=a^x and y=a^(x-k). |
| @yROTz Solve the equation 4^x@-@2^(x+2)@=@32 using a graph | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@ @@@@@@@@Draw the graphs of y=4^x and y=2^(x+2) +32. @@@(1) Create the following correspondence table on a worksheet. @@@Reference @@@@@@Please refer to yROPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Merkern @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 10.0 @@@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete the points(markers) in the correspondence table from the graph. @@@@@@@ Left-click the graph area to activare. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth linen @@@@@@ 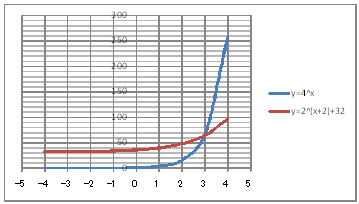 @@@Consideration @@@@@@Solve the equation 4^x-2^(x+2)=32 from the intersection of the graphs y=4^x and y=2^(x+2)+32 |
| @yROUz Solve the inequality 9^x@<@2¥3^x@+@3 using a graph. | ||||||||||||||||||||||||||||
| @Procedure @@@@@@@@Draw the graphs y=9^x and y=2¥3^x+3 @@@(1) Create the following correspondence table on a worksheet. @@@Reference @@@@@@Please refer to yROPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D16 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line and Marker] @@@@@@B Expand the graph area vertially by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is draw. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Auxliary add gridlines @@@(4) Delete the points(markers) in the correspondence table from the graph. @@@@@@@ Left-click the graph area to activate it. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 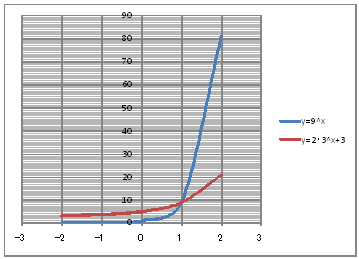 @@@Consideration @@@@@@Solve the inequality 9^x@<@2¥3^x@+@3 from the intersection of the graphs of y=9^x and y=2¥3^x+3. @ |
| @yROVz Compare the size of 8^(1/4) , 16^(1/3) , 64^(1/5) using a graph. | ||||||||||||
| @Procedure @@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet@@@@@@@ @@@@@@@Enter the information in cells B12 , B13 , and B14 as shown in the worksheet above. @@@@@@@Enter =POWER(8,1/4) in Cell C12. @@@@@@@Enter =POWER(16,1/3) in Cell C13. @@@@@@@Enter =POWER(64,1/5) in Cell C14 @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B12:C14 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mVertical barn¨m2-D vertical bar clustern @@@@@@ 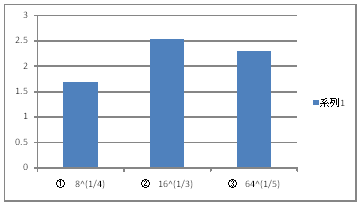 @@@Consideration @@@@@@Compare the sizes of 8^(1/4)@16^(1/3)@64^(1/5) from the bar graphs of 8^(1/4) , 16^(1/3) , and 64^(1/5) @@@@@@ |
| @To table of contents@ |
| @ySOPz Draw a graph of the logarithmic functions of y=log(2)x , y=log(3)x , y=log(4)x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Drag the cell range B12:B20 and right-click , and select Cell formatting. @@@@@@@Select a number from the classification and set the number of decimal places to 5. @@@@@@@Enter 1/16 in half-width in cell B12 (Displayed as a decimal). @@@@@@@Enter data in the cell range B13:B20 using half-width characters as shown in the worksheet above. @@@@@@@Enter =LOG(B12,2) in half-width in cell C12. @@@@@@@Enter =LOG(B12,3) in half-width in cell D12. @@@@@@@Enter =LOG(B12,4) in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C20 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E20 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line and Markern @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points(markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 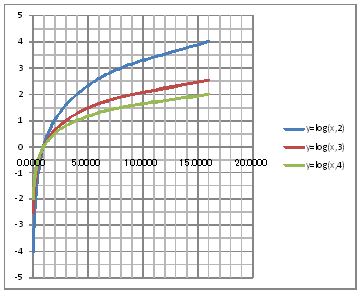 @@@Consideration 1 @@@@@@Find the coordinates of point which the graphs of y=log(2)x , y=log(3)x , and y=log(4)x commonly pass through. @@@Consideration 2 @@@@@@Find the common asymptote for the graphs of y=log(2)x , y=log(3)x , and y=log(4)x. @@@Consideration 3 @@@@@@State the difference between the graphs of y=log(2)x , y=log(3)x , and y=log(4)x. @ |
| @ySOQz Draw a graph of the logarithmic functions of y=log(1/2)x , y=log(1/3)x , and y=log(1/4)x. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet. @@@Reference @@@@@@Refer to ySOPz how to complete the wprksheet.
@@@(2) Draw a graph from the correspondence table in (1) avobe. @@@@@@@ Drag and select the cell range B11:E20 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line and Markern @@@@@@B Expand the graph area vertically by dragging the top and bottom of graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 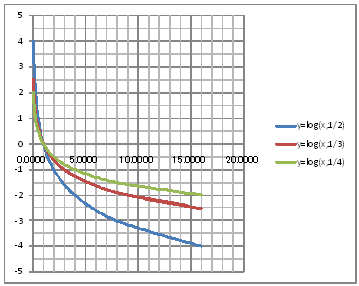 @@@Consideration 1 @@@@@@Find the coordinates of the point that the graphs of y=log(1/2)x , y=log(1/3)x and , y=log(1/4)x pass commonly through. @@@Consideration 2 @@@@@@Find the common asymptote for the graphs of y=log(1/2)x , y=log(1/3)x and , y=log(1/4)x. @@@Consideration 3 @@@@@@State the difference between the graphs of y=log(1/2)x , y=log(1/3)x and , y=log(1/4)x. |
| @ySORz Draw a graph of the logarithmic functions of y=log(2)x and y=log(1/2)x. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following corresspondence table on the worksheet. @@@Referrence @@@@@@Please refer to ySOPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mSmooth line and Markern @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 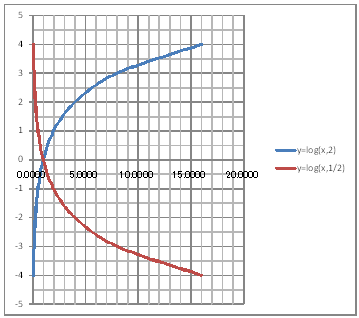 @@@Consideration 1 @@@@@@@State the positional relationship of the graphs of y=log(2)x and y=log(1/2)x. @@@Consideration 2 @@@@@@@In general , what can be said about the positional relationship between the graphs of y=log(2)x and y=log(1/2)x. |
| @ySOSz Draw a graph of the logarithmic functions of y=log(2)x and y=log(2)(1/x) | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to ySOPz how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correspndence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line and Markersn @@@@@@B Expand the graph area vertically by dragging the top and bottom of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 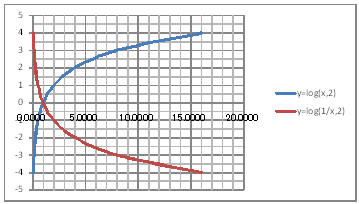 @@@Consideration 1 @@@@@@@State the positional relationship between the graphs of y=log(2)x and y=log(2)(1/x). @@@Consideration 2 @@@@@@In general , what can be said about the positional relationship between the graphs of y=log(a)x and y=log(a)(1/x). @ |
| @ySOTz Solve equation log(10)x+log(10)(x-3)=1 using graphs. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@Draw graphs of y=log(10)x and y=-log(10)(x-3)+1. @@@(1) Create the following correspondence table on the worksheet. @@@Reference @@@@@@Please refer to y401z how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D20 in the correpondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line and markern @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.1 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 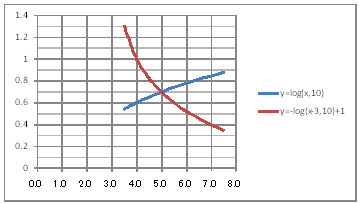 @@@Consideration @@@@@@@Solve equation log(10)x+log(10)(x-3)=1 from the intersection of the graphs of y=log(10)x and y=-log(10)(x-3)+1. |
| @ySOUz Solve inequality log(3)(x-3)+log(3)(x-5)<1 using a graph. | ||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@log(3)(x-3) < -log(x-5)+1 @@@@@@@@@@Draw graphs of y=log(3)(x-3) and y=-log(3)(x-5)+1. @@@(1) Create the following correspondence table on a worksheet. @@@Reference @@@@@Please refer to y401z how to complete the worksheet.
@@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D18 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line and Markern @@@@@@B Expand the graph area vertically by dragging the top and bottom edges of the graph area. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.00 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridline @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.1 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridline @@@(4) Delete points (markers) in the correspondence table from the graph. @@@@@@@ Left-click on the graph area to activate it. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@ 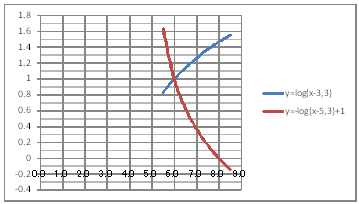 @@@Consideration @@@@@@@Solve inequality log(3)(x-3)+log(3)(x-5) < 1 from the intersection of the graphs of y=log(3)(x-3) and y=-log(3)(x-5)+1 @@@@@@ |
| @ySOVz Compare the size of 1/2, -log(2)(1/3) , and log(1/2)7 using the graphs. | ||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete a worksheet abovet @@@@@@@Enter data into cells B12 , B13 , and B14 as shown in the worksheet above. @@@@@@@Drag the cell range C12:C14 , right-click , and select Cell Formatting. @@@@@ @ Select a number from the crassification and set the number of decimal places to 5. @@@@@@@Enter 1/2 in half-width in cell C12. @@@@@@@Enter =-1*LOG(1/3,2) in half-width in cell C13. @@@@@@@Enter =LOG(7,1/2) in half-width in cell C14. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B12:C14 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mVertical barn¨m2-D vertical bar clustern @@@@@@ 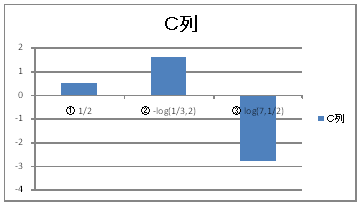 @@@Consideration @@@@@@From the bar graphs of 1/2 , -log(2)(1/3) , and log(1/2)7 , compare the sizes of 1/2 , -log(2)(1/2) , and log(1/2)7. |
| @To table of contents@ |
| @yTOPz Draw a circle x^2+y^2+6x-8y-11=0 | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure@ @@@@@@@@@@x^2+y^2+6x-8y-11=0 @@@@@@@@@@x^2+6x+9+y^2-8y+16=11+9+16 @@@@@@@@@@(x+3)^2+(y-4)^2=36 , center(-3,4 ) , radius 6 @@@@@@@@@@(y-4)^2=36-(x+3)^2 @@@@@@@@@@y-4=+ã{36-(x+3)^2} , -ã{36-(x+3)^2} @@@@@@@@@@y=4+ã{36-(x+3)^2} , 4-ã{36-(x+3)^2} @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -9 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B132 , Right-click , and select Paste. @@@@@@@Enter =4+SQRT(36-(B12+3)^2) in half-width in cell C12. @@@@@@@Enter =4-SQRT(36-(B12+3)^2) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , Right-click , and select Copy. @@@@@@@Drag the cell range C13:C132 , Right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D132 in the correspondence table of (1) above. @@@@@@A mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area to stretch and adjust. @@@(3) Arrange the xy plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@@@@ 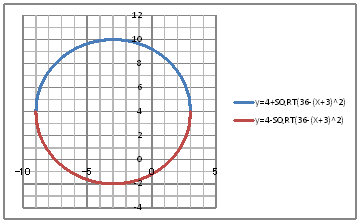 @@@Consideration @@@@@@@Make sure that it is a circle with center(-3,4) and radius 6. @ |
| yTOQz Find the coordinates of the common point between circle x^2+y^2=5 and straight line y=-x+1 by drawing a graph. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -2.236 in half-width in cell B12. @@@@@@@Enter -2.2 in half-width in cell B13. @@@@@@@Enter =B13+0.1 in half-width in cell B14. @@@@@@@Right-click on cell B14 and select Copy. @@@@@@@Drag the cell range B15:B57 , right-click , and select Paste. @@@@@@@Enter 2.236 in half-width in cell C12. @@@@@@@Enter =SQRT(5-B12^2) in half-width in cell C12. @@@@@@@Enter =-SQRT(5-B12^2) in half-width in cell D12. @@@@@@@Enter =-B12+1 in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C58 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E58 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@  @@@Consideration @@@@@@Find the coordinates of the common point from the graphs circle x^2+y^2=5 and straight line y=-x+1. @ |
| yTORz Draw an ellipse whose sum of distances from two fixed points (3,0) and (-3,0) is 10. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@Let x^2/a^2+y^2/b^2=1 be the ellipse to seek. @@@@@@@@@@R @@@@@@@@@@Since QPO , T @@@@@@@@@@Since c=ã(a^2-b^2) , 3=ã(5^2-b^2) @@@@@@@@@@S @@@@@@@@@@Therefore , @@@@@@@@@@@@x^2/5^2 + y^2/4^2 = 1 , y=4ã(1 - x^2/25) , y=-4ã(1 - x^2/25) @@@(1) Create the following correspondence table in a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -5 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B112 , right-click , and select Paste. @@@@@@@Enter =4*SQRT(1-B12^2/25) in half-width in cell C12. @@@@@@@Enter =-4*SQRT(1-B12^2/25) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C112 , right-click , and select Paste. @@@(2) Drag a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D112 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the right and left edges of the graph areas holizontally to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 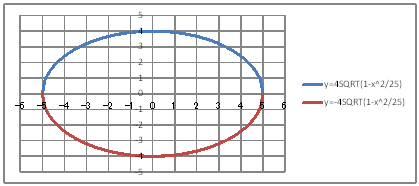 @@@Consideration @@@@@@@Make sure that ellipse x^2/5^2 + y^2/4^2 = 1 is drawn. |
| yTOSz Draw a parabola whose distance from rhe fixed point (2,0) is equal to the distance from the straight line x=-2. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@Let y^2=4px be the parabola to seek. @@@@@@@@@@Since p=2 , y^2=8x @@@@@@@@@@y=2ã(2x) , y=-2ã(2x) @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B12. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B52 , right-click , and select Paste. @@@@@@@Enter =2*SQRT(2*B12) in half-width in cell C12. @@@@@@@Enter =-2*SQRT(2*B12) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C52 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D52 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of graph area vertically to stretch and adjust. @@@(3) Arrange the coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 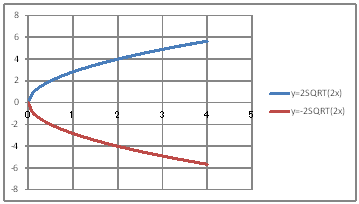 @@@Consideration @@@@@@@Make sure that parabola y^2=8x is drawn. |
| @yTOTz Draw a hyperbola whose dtfference between distances from two fixed points (5,0) and (-5,0) is 6. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@Let x^2/a^2 - y^2/b^2 = 1 be the hyperbola to seek. @@@@@@@@@@Since c=5 , 2a=6 , c=ã(a^2+b^2) , a=3 , b=4 @@@@@@@@@@Therefore @@@@@@@@@@@@@x^2/3^2 - y^2/4^2 = 1 , y=4ã(x^2/9 - 1) , y=-4ã(x^2/9 - 1) @@@(1) Create the following correspondence table in a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 10 in half-width in cell B12. @@@@@@@Enter =B12-0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B82 , right-click , and select Paste. @@@@@@@Enter -3 in half-width in cell B84. @@@@@@@Enter =B84-0.1 in half-width in cell B85. @@@@@@@Right-click on cell B85 and select Copy. @@@@@@@Drag the cell range B86:B154 , right-click , and select Paste. @@@@@@@Enter =4*SQRT(B12^2/9-1) in half-width in cell C12. @@@@@@@Enter =-4*SQRT(B12^2/9-1) in half-width in cell D12 @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C154 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@See y504z @@@(3) Arrange the xy coordinate plane on whic the graph is drawn. @@@@@@@ Right-click on the numbers on x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on x-axis ¨ Add auxiliary gridlines @@@@@@A Right-click on the numbers on y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on y-axis ¨ Add auxiliary gridlines @@@@@@ 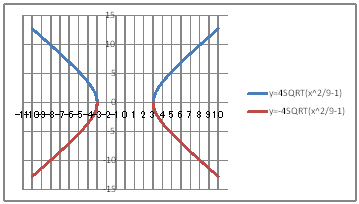 @@@Consideration @@@@@@@Make sure that hyperbola x^2/3^2 - y^2/4^2 = 1 is drawn. |
| @To table of contents@ |
| @yUOPz Draw graphs of function y=-2x^3+6x+1 and y'=-6x^2+6. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet above.t @@@@@@@Enter -3 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B72 , right-click and , select Paste. @@@@@@@Enter =-2*B12^3+6*B12+1 in half-width in cell C12. @@@@@@@Enter =-6*B12^2+6 in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C72 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:D72 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen. @@@@@@B Drag the top and bottom area of the graph area vertically to strech and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 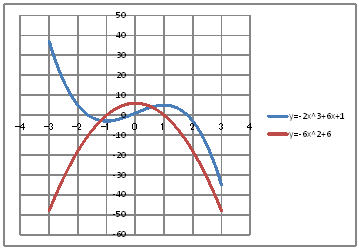 @@@Consideration 1 @@@@@@@When y'<0 , what does the graph of y=-2x^2+6x+1 look like ? @@@Consideration 2 @@@@@@@When y'>0 , what does the graph of y=-2x^2+6x+1 look like ? @@@Consideration 3 @@@@@@@When y'=0 , what does the graph of y=-2x^2+6x+1 look like ? @ |
| yUOQz Find the maximam and minimum values by drawing a graph of function y=2x^3-3x^2-12x-6 (-2 x 4) | |||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -2 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B72 , right-click , and select Paste. @@@@@@@Enter =2*B12^3-3*B12^2-12*B12-6 in half-width in cell C12. @@@@@@@Right-click on cell C12 and select Copy. @@@@@@@Drag the cell range C13:C72 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C72 in the orrespondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@@@@B Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Scale interval Fixed 5.0 @@@@@@¨ close @@@@@@ 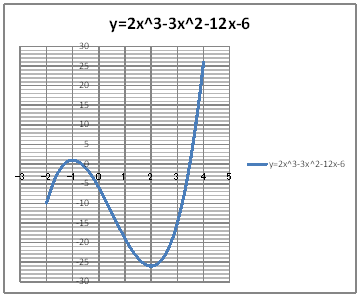 @@@Consideration 1 @@@@@@@ Find the maximum value when -2 x 4 from the graph. @@@Consideration 2 @@@@@@@Find the minimum value when -2 x 4 from the graph. @ |
| yUORz Find the number of different real solutions for cubic equation x^3-3x^2-a=0 using a graph. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@x^3-3x^2=a @@@@@@@@@@Draw graphs of y=x^3-3x^2 and y=a. @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter a= in cell B81. @@@@@@@Enter 1 in half-width in cell C81. @@@@@@@Enter -2 in half-width in cell B12 @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cellrange B14:B72 , right-click , and select Paste. @@@@@@@Enter =B12^3-3*B12^2 in half-width in cell C12. @@@@@@@Enter =$C$8 in half-width in cell D12. @@@@@@@Drag the cellrange C12:D12 , right-click , and select Copy. @@@@@@@Drag the cellrange C13:C72 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) avove. @@@@@@@ Drag and select the cell range B11:D72 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 1.0 @@@@@@¨ close ¨Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@@@@ 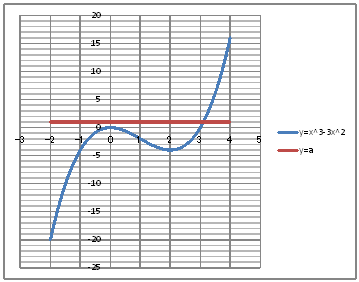 @@@Consideration 1 @@@@@@@When a=1 , a=-5 , find the number of different real solutions. @@@Consideration 2 @@@@@@@When a=0 , a=-4 , find the number of different real solutions. @@@Consideration 3 @@@@@@@When a=-2 , find the number of different real solutions. @@@Consideration 4 @@@@@@@How does the number of different real solutions change depending on the value of the constant a ? |
| yUOSz When x0 , draw a graph to confirm that the inequality x^3-3x^2+40. | |||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B44 , right-click , and select Paste. @@@@@@@Enter =B12^3-3*B12^2+4 in half-width in cell C12. @@@@@@@Right-click on cell C12 and select Copy. @@@@@@@Drag the cell range C13:C44 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C44 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 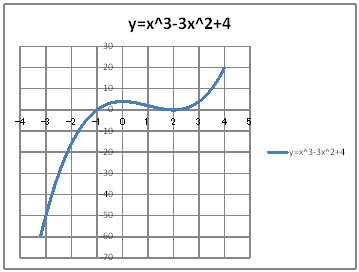 @@@Consideration @@@@@@@When x0 , @@@@@@@look at the graph and confirm that the inequality x^3-3x^2+40 holds true. |
| @yUOTz Draw a graph of the curve y=logx and the tangent and normal at point(1,0) on it. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@Tangent F |OPi|Pj@@@@@|P @@@@@@@@@@Normal F |O|Pi|Pj@@ @|{P @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0.05 in half-width in cell B12. @@@@@@@Enter =B12+0.05 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B111 and right-click , and select Paste. @@@@@@@Enter =LN(B12) in half-width in cell C12. @@@@@@@Enter =B12-1 in half-width in cell D12. @@@@@@@Enter =-B12+1 in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 and right-click , and select Copy. @@@@@@@Drag the cell range C13:C111 and right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E111 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Arrange the top and bottom of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 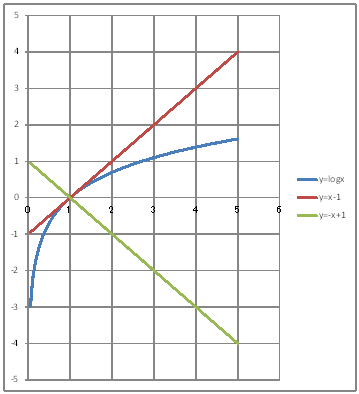 @@@Consideration 1 @@@@@@@Make sure that y=x-1 is tangent to point (1,0) on y=logx. @@@Consideration 2 @@@@@@@Make sure that y=-x+1 is normal to point (1,0) on y=logx. |
| @yUOUz Draw the graph of ellipse x^2/4 + y^2 = 1 and the tangent at the point (6/5,4/5) on it. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@Since y^2 = 1 - x^2/4 , y=}ã(1-x^2/4) @@@@@@@@@@Since the tangent formula , x/4 ~ 6/5 + y ~ 4/5 = 1 @@@@@@@@@@Therefore , tangent : y=-(3/8)x + 5/4 @@@@@@@@@@Draw the graphs of y = ã(1-x^2/4) , y = -ã(1-x^2/4) , and y = -3/8 + 5/4 @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -2 in half-width in cell B12. @@@@@@@Enter =B12+0.05 in half-width in cell B13. @@@@@@@Right-click on cell B13 and select Copy. @@@@@@@Drag the cell range B14:B32 , right-click , and select Paste. @@@@@@@Enter =SQRT(1-B12^2/4) in half-width in cell C12. @@@@@@@Enter =-SQRT(1-B12^2/4) in half-width in cell D12. @@@@@@@Enter =-3*B12/8+5/4 in half-width in cell E12. @@@@@@@Drag the cell range C12:E12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C92 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:E92 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth line] @@@@@@B Drag the left and right edges of graph area horizontally and the top and bottom edges of graph area vertically to strech and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 ¨ close @@@@@@¨ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.2¨ close @@@@@@¨ Right-click on the numbers on the x-axis ¨ Add auxiliary gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Axis formatting @@@@@@¨ Auxiliary scale interval Fixed 0.2 ¨ close ¨ Right-click on the numbers on the y-axis @@@@@@¨ Add auxiliary gridlines @@@@@@ 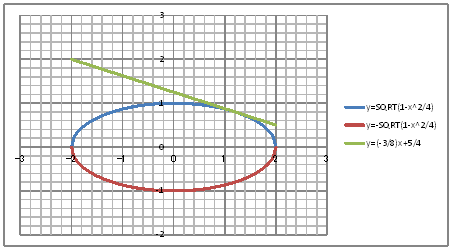 @@@Consideration @@@@@@Make sure that y=(-3/8)x+5/4 is the tangent to the point (6/5,4/5) on the ellipse x^2/4+y^2=1. |
| @To table of contents@ |
| @yVOPz Draw a graph of function y=xã(9-x^2). | |||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -3 in half-width in the cell B12. @@@@@@@Enter =B12+0.1 in half-width in the cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B72 , right-click , and select Paste. @@@@@@@Enter =B12*SQRT(9-B12^2) in half-width in the cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C72 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C72 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 1.0 @@@@@@¨ close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@A Right-click on the numbers on the y-axis ¨ Axis formatting ¨ Auxiliary scale interval Fixed 0.5 @@@@@@¨ close ¨ Right-click on the numbers on the y-axis ¨ Add auxiliary gridlines @@@@@@ 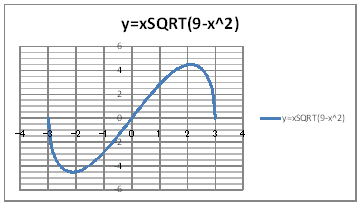 @@@Consideration 1 @@@@@@@Find the local maximum from the graph. @@@Consideration 2 @@@@@@@Find the local minimum from the graph. @@@Consideration 3 @@@@@@@Find the maximum value from the graph. @@@Consideration 4 @@@@@@@Find the minimum value from the graph. @ |
| yVOQz For 0 x 2Î , draw the graph of the function y=x+2sinx. | |||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and select Paste. @@@@@@@Enter =RADIANS(B12)+2*SIN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C192 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Axis formatting ¨ Scale interval Fixed 60.0 @@@@@@¨ Close ¨ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 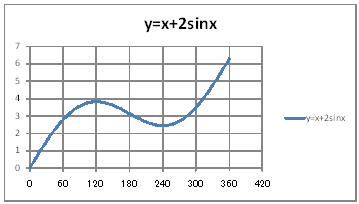 @@@Consideration 1 @@@@@@@Use a graph to find the value of x that takes the local maximum value when 0 x 2Î.@Then caluculate the local maximum value. @@@Consideration 2@ @@@@@@@Use a graph to find the value of x that takes the local miniimum value when 0 x 2Î.@Then caluculate the local minimum value. @@@Consideration 3 @@@@@@@Use a graph to find the value of x that takes the maximum value when 0 x 2Î.@Then caluculate the maximum value. @@@Consideration 4 @@@@@@@Use a graph to find the value of x that takes the miniimum value when 0 x 2Î.@Then caluculate the minimum value. @ |
| yVORz Draw a graph of the function y=x+ã(4-x^2) | |||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -2 in half-width in cell B12. @@@@@@@Enter =B12+0.1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B52 and right-click , and select Paste. @@@@@@@Enter =B12+SQRT(4-B12^2) in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C52 and right-click , and select Paste. @@@@@@@Enter 2 in half-width in cell C52. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C52 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 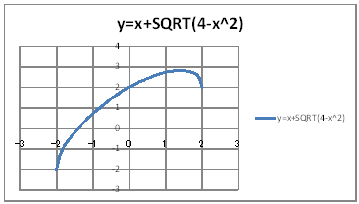 @@@Consideration @@@@@@@Find the minimum value and the value of x at that time from the graph. |
| yVOSz When -1 x 1 , draw a graph of the function y=e^(2x)-2e^x+1 | |||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter -1 in half-width in cell B12. @@@@@@@Enter =B12+0.05 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B52 , right-click , and select Paste. @@@@@@@Enter =EXP(2*B12)-2*EXP(B12)+1 in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C52 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B11:C52 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Riht-click on the numbers on the x-axis ¨ Add gridlines @@@@@@ 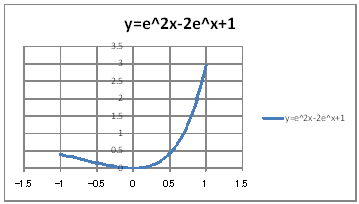 @@@Consideration 1 @@@@@@@When -1 x 1 , find the maximum value and the value of x at the time using the graph. @@@Consideration 2 @@@@@@@When -1 x 1 , find the minimum value and the value of x at the time using the graph. @ |
| @To table of contents@ |
| @yWOPz Find the area enclosed by the curve y=x^2 , the x-axis , and the straight line x=1 using the piecewise method. | ||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0.01 in halh-width in cell B12. @@@@@@@Enter =B12+0.01 in halh-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B111 , right-click , and select Paste. @@@@@@@Enter =B12^2 in halh-width in cell C12. @@@@@@@Enter =0.01*C12 in halh-width in cell D12. @@@@@@@Right-click the cell range C12:D12 , and select Copy. @@@@@@@Drag the cell range C13:C111 , right-click , and select Paste. @@@(2) Find the piecewisw from the correspondence table in (1) abobe. @@@@@@@ Find the sum of the cell range D12:D111 in the correspondence table in (1) above. @@ @@@@@@Enter =SUM(D12:D111) in half-width in cell D112 .of the worksheet. @@@Consideration 1 @@@@@@@Calcurate the following definite integral and find the area enclosed by the curve y=x^2 , the x-axis , and the straight line x=1. @@@@@@@ @@@Consideration 2 @@@@@@@Compare the value of the definite integral obtained in consideration 1 with the value of D112 , which is the sum of the cell range D12:D111 in the correspondence table of the worksheet. @ |
| @yWOQz Draw a graph of cycloid |AP| (O QÎ). Also , find its length. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 0 in half-width in cell B12. @@@@@@@Enter =B12+2 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B192 , right-click , and select Paste. @@@@@@@Enter =RADIANS(B12)-SIN(RADIANS(B12)) in half-width in cell C12. @@@@@@@Enter =1-COS(RADIANS(B12)) in half-width in cell D12 @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:D192 , right-click , and select Paste. @@@@@@@Enter =C13-C12 in half-width in cell E13. @@@@@@@Enter =D13-D12 in half-width in cell F13. @@@@@@@Enter =SQRT(E13^2+F13^2) in half-width in cell G13. @@@@@@@Drag the cell range E13:G13 , right-click , and select Copy. @@@@@@@Drag the cell range E14:E192 , right-click , and select Paste. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range C11:D192 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mSmooth linen @@@@@@B Drag the top and bottom edges of the graph area vertically to stretch and adjust. @@@(3) Arrange the xy-coordinate plane on which the graph is drawn. @@@@@@@ Right-click on the numbers on the x-axis ¨ Add gridlines @@@(4) Find the length of the cycloid from the correspondence table in (1) above. @@@@@@@ Find the sum of the cell range G13:G192 in the correspondence table of (1) above. @@ @@@@@@Enter =SUM(G13:G192) in half-width in cell G193 of the worksheet. @@@@@@ 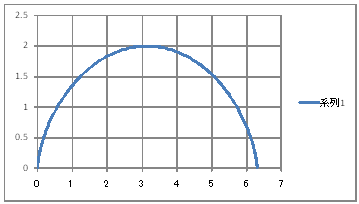 @@@Consideration 1 @@@@@@@Calculate the following definite integral and find the length of the cycloid |AP| (O QÎ) @@@@@@@ 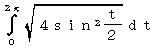 @@@Consideration 2 @@@@@@@Compare the value of the definite integral obtained in Consideration 1 with the value of cell G193 , which is the sum of the cell range G13:G192 in the correspondence table of the worksheet. @ |
| @To table of contents@ |
| @yXOPz Find the general terms of the arithmetic progression where the 3rd term is 5 and the 12th term is 59. | |||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@Let@ @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@If you solve @ and A simultaneously , |VAU @@@@@@@@@@Therefore , @@@@@@@@@@@ @ @ @ @ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B111 , right-click , and select Paste. @@@@@@@Enter =6*B12-13 in half-width in cell C12. @@@@@@@Right-click cell C12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C111 , right-click , and select Paste. @@@Consideration 1 @@@@@@@Solving for a(n)=6n-13=143 gives n=26. @@@@@@@Check on the worksheet that 143 is the 26th term. @@@Consideration 2 @@@@@@@ @@@@@@ Check on the worksheet that the 96th term is 563. @ |
| @yXOQz Find the general terms of the geometric progression where the 3rd term is 12 and the 7th term is 192. | ||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@ @Let @@@@@@@@@@ @@@@@@@@@@ @@@@@@@@@@Solving @ and A simultaneously gives RA}Q @@@@@@@@@@Therefore , @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter the information in the cell range B11:D111 as shown in the table above. @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 , right-click , and select Paste. @@@@@@@Enter =3*2^(B12-1) in half-width in cell C12. @@@@@@@Enter =3*(-2)^(B12-1) in half-width in cell D12. @@@@@@@Drag the cell range C12:D12 , right-click , and select Copy. @@@@@@@Drag the cell range C13:C46 , right-click , and select Paste. @@@Consideration 1 @@@@@@@ @@@@@@@ @@@@@@@Check on the worksheet that the 8th term is 384 and -384. @@@Consideration 2 @@@@@@@Solving a(n)=3*2^(n-1)=786432 gives n=19. @@@@@@@Solving a(n)=3*(-2)^(n-1)=786432 gives n=19. @@@@@@@Check on the worksheet that 786432 is the 19th term. @ |
| @yXORzFind the sum from the first term to the nth term of an arithmetic progression where the first term is 50 and the commom difference is -6. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Drag the cell range B11:E11 , right-click and select Cell formatting. @@@@@@@Select Tablar format ¨ Classification string¨ OK @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B61 , right-click , and select Paste. @@@@@@@Enter =-6*B12+56 in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C61 , right-click , and select Paste. @@@@@@@Enter 50 in half-width in cell D12. @@@@@@@Enter =D12+C13 in half-width in cell D13. @@@@@@@Right-click on the cell D13 and select Copy. @@@@@@@Drag the cell range D14:D61 , right-click , and select Paste. @@@@@@@Enter =-3*B12^2+53*B12 in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy. @@@@@@@Drag the cell range E13:E61 , right-click , and select Paste. @@@Consideration 1 @@@@@@@Make sure that the sum in column D of the worksheet matches -3n^2+53n in column E. @@@Consideration 2 @@@@@@@ @@@@@@@ @@@@@@@Therefore , when n=9 , it is maximum. @@@@@@@Check on the worksheet that when n=9 , it is the maximum. |
| @yXOSzFind the sum from the first term to the nth term of a geometric progression with an initial term of 1/2 and a common ratio of 2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the woksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 , right-click , and select Paste. @@@@@@@Enter =2^(B12-2) in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range B13:C46 , right-click , and select Paste. @@@@@@@Enter 0.5 in half-width in cell D12. @@@@@@@Enter =D12+C13 in half-width in cell D13. @@@@@@@Right-click on the cell D13 and select Copy. @@@@@@@Drag the cell range D14:D46 , right-click , and select Paste. @@@@@@@Enter =(2^B12-1)/2 in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy @@@@@@@Drag the cell range E13:E46 , right-click , and select Paste. @@@Consideration 1 @@@@@@@Make sure that the sum in column D of the worksheet matches (2^n-1)/2 in column E. @@@Consideration 2 @@@@@@@ @@@@@@@Solving this gives n=11. @@@@@@@Check on the sheet that the fist term the sum exceedds 1000 is the sum up to the 11th term. @ |
| @yXOTz Find the sum from 1^2 to n^2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 ,right-click . and select Paste. @@@@@@@Enter =B12^2 in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C46 ,right-click . and select Paste. @@@@@@@Enter 1 in half-width in cell D12. @@@@@@@Enter =D12+C13 in half-width in cell D13. @@@@@@@Right-click on the cell D13 and select Copy. @@@@@@@Drag the cell range D14:D46 ,right-click . and select Paste. @@@@@@@Enter =B12*(B12+1)*(2*B12+1)/6 in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy. @@@@@@@Drag the cell range E13:E46 ,right-click . and select Paste. @@@Consideration @@@@@@@Make sure that the sum in column D of the worksheet matches n(n+1)(2n+1)/6 in column E. |
| @yXOUz Find the sum from 1^3 to n^3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@ @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 , right-click , and select Paste. @@@@@@@Enter =B12^3 in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C46 , right-click , and select Paste. @@@@@@@Enter 1 in half-width in cell D12. @@@@@@@Enter =D12+C13 in half-width in cell D13. @@@@@@@Right-click on the cell D13 and select Copy. @@@@@@@Drag the cell range D14:D46 , right-click , and select Paste. @@@@@@@Enter =(B12*(B12+1)/2)^2 in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy. @@@@@@@Drag the cell range E13:E46 , right-click , and select Paste. @@@Consideration @@@@@@@Make sure that the sum in column D of the worksheet matches {n(n+1)/2}^2 in column E. |
| @yXOVzFind the general term of the following sequence. @@@@@@RCSCUCPOCPWCRSCEEE |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on the worksheet.
@@@Referrence @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 , right-click , and select Paste. @@@@@@@Enter =2^(B13-2) in half-width in cell C13. @@@@@@@Right-click on the cell C13 and select Copy. @@@@@@@Drag the cell range C14:C46 , right-click , and select Paste. @@@@@@@Enter 3 in half-width in cell D12. @@@@@@@Enter =D12+C13 in half-width in cell D13. @@@@@@@Right-click on the cell D13 and select Copy. @@@@@@@Drag the cell range D14:D46 , right-click , and select Paste. @@@@@@@Enter =2^(B12-1)+2 in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy. @@@@@@@Drag the cell range E13:E46 , right-click , and select Paste. @@@Consideration @@@@@@@Make sure that the sum in column D of the worksheet matches 2^(n-1)+2 in column E. |
| @yXOWzFind the general term of the sequence {a(n)} defined by the following
recurrence formula. @@@@@@ @@@@@@ |
||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@When a(n+1) =2a(n)+3 is transformed , a(n+1)+3=2{a(n)+3} @@@@@@@@@@Sequence {a(n)+3} is a geometric progression where the first term is 4 and the common ratio is 2. @@@@@@@@@@Therefore , a(n)+3=4~2^(n-1)=2^(n+1) @@@@@@@@@@a(n)=2^(n+1)-3 @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 , right-click , and select Paste. @@@@@@@Enter 1 in half-width in cell C12. @@@@@@@Enter =2*C12+3 in half-width in cell C13. @@@@@@@Right-click on the cell C13 and select Copy. @@@@@@@Drag the cell range C14:C46 , right-click , annd select Paste. @@@@@@@Enter =2^(B12+1)-3 in half-width in cell D12. @@@@@@@Right-click on the cell D12 and select Copy. @@@@@@@Drag the cell range D13:D46 , right-click , annd select Paste. @@@Reference @@@@@@@Make sure that the recurrence formula in column C of the worksheet matches 2^(n+1)-3 in column D. |
| @yXOXz Find the general term of the sequence {a(n)} defined by the following
recurrence formula. @@@@@@@@ @@@@@@@@ @@@@@@@@ |
||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@Solve this recurrence formula to find the general term. @@@@@@@@@@ 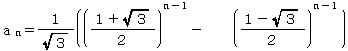 @ @@@@@@@@@@@ @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the cell B13 and select Copy. @@@@@@@Drag the cell range B14:B46 , right-click , and select Paste. @@@@@@@Enter 0 in half-width in cell C12. @@@@@@@Enter 1 in half-width in cell C13. @@@@@@@Enter =(2*C13+C12)/2 in half-width in cell C14 @@@@@@@Right-click on the cell C14 and select Copy. @@@@@@@Drag the cell range C15:C46 , right-click , and select Paste. @@@@@@@Enter =(((1+SQRT(3))/2)^(B12-1)-((1-SQRT(3))/2)^(B12-1))/SQRT(3) in half-width in cell D12. @@@@@@@Right-click on the cell D12 and select Copy. @@@@@@@Drag the cell range D13:D46 , right-click , and select Paste. @@@Consideration @@@@@@@Make sure that the recurrence formula in column C of the worksheet matches the general term in column D. |
| @yXPOz Consider the Febonacci sequence determined by the following recurrence
formula. @@@@@@@ @@@@@@@ @@@@@@@ |
||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter 1 in half-width in cell B12. @@@@@@@Enter =B12+1 in half-width in cell B13. @@@@@@@Right-click on the B13 and select Copy. @@@@@@@Drag the cell range B14:B61 , right-click , and select Paste. @@@@@@@Enter 1 in half-width in cell C12. @@@@@@@Enter 1 in half-width in cell C13. @@@@@@@Enter =C12+C13 in half-width in cell C14. @@@@@@@Right-click on the C14 and select Copy. @@@@@@@Drag the cell range C15:C61 , right-click , and select Paste. @@@@@@@Enter =C13/C12 in half-width in cell D13. @@@@@@@Right-click on the D13 and select Copy. @@@@@@@Drag the cell range D14:D61 , right-click , and select Paste. @@@Consideration @@@@@@@Make sure that the value of (the 50th term/ the 49th term) in column D of the worksheet is close to the golden ratio (1+ã5)/2à1.618033989. |
| @To table of contens@ |
| @y1001z Inverse trigonometric functions and Conversion from arc degree
method to degree method @@@@@@i`rhm functionA`bnr functionA`s`m functionAcdfqddr functionj |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet above.t @@@@@@@Drag the cell range B12:B20 , right-click and select Cell formatting. @@@@@@@Select Display format ¨ Classification string ¨ OK @@@@@@@Enter data in the cell range B12:B20 as shown in the table above @@@@@@@Drag the cell range D12:D20 , right-click ,and select Cell formatting @@@@@@@Select Display format ¨ Classification string ¨ OK @@@@@@@Enter data in the cell range D12:D20 as shown in the table above @@@@@@@Drag the cell range F12:F20 , right-click ,and select Cell formatting @@@@@@@Select Display format ¨ Classification string ¨ OK @@@@@@@Enter data in the cell range F12:F18 as shown in the table above @@@@@@@Enter =DEGREES(ASIN(-1)) in cell C12. @@@@@@@Similarly , enter =DEGREES(ASIN(value in the same row of column B)) in half-width from C13 to C20 @@@@@@@Enter =DEGREES(ACOS(1)) in cell E12. @@@@@@@Similarly , enter =DEGREES(ACOS(value in the same row of column D)) in half-width from E13 to E20 @@@@@@@Enter =DEGREES(ATAN(-SQRT(3))) in cell G12. @@@@@@@Similarly , enter =DEGREES(ACOS(value in the same row of column F)) in half-width from G13 to G18 @@@About functions @@@@@@@`rhm function¥¥¥ ASIN(real number 1) @@@@@@@@@@Return the angle of SIN that has a real number 1 in radians. @@@@@@@`bnr function¥¥¥ ACOS(real number 1) @@@@@@@@@@Return the angle of COS that has a real number 1 in radians. @@@@@@@`s`m function¥¥¥ ATAN(real number 1) @@@@@@@@@@Return the angle of TAN that has a real number 1 in radians. @@@@@@@cdfqddr function¥¥¥ DEGREES(WA) @@@@@@@@@@Converts an angle in radians to an angle in degrees. @ |
| @y1002z Sum of squares of complex numbers @@@@@@irtlrp functionj |
||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Drag the cell range B11:B20 , right-click , and select Cell formatting. @@@@@@@Select Display format ¨ Classification string ¨ OK. @@@@@@@Enter data in the cell range B11:B20 as shown in the table above. @@@@@@@Enter =SQRT(0) in half-width in cell C12. @@@@@@@Enter =SQRT(1) in half-width in cell C13. @@@@@@@Enter =SQRT(2) in half-width in cell C14. @@@@@@@Enter =SQRT(3) in half-width in cell C15. @@@@@@@Enter =SQRT(4) in half-width in cell C16. @@@@@@@Enter =SQRT(5) in half-width in cell C17. @@@@@@@Enter =SQRT(6) in half-width in cell C18. @@@@@@@Enter =SQRT(7) in half-width in cell C19. @@@@@@@Enter =SQRT(8) in half-width in cell C20. @@@@@@@Enter =SUMSQ(C12,C13) in half-width in cell D13. @@@@@@@Right-click on the cell D13 and select Copy. @@@@@@@Drag the cell range D14:D20 , right-click , and select Paste. @@@About function @@@@@@@rtlrp function¥¥¥ SUMSQ(real number 1Creal number 2) @@@@@@@@@@ Returns the value of (real number 1)^2 + (real number 2)^2 @ |
| @y1003z Four arithmetic calculations of complex numbers <sum , difference
, product , quotient> and display in complex number format @@@@@@ihlrtl function Ahlrta function Ahloqnctbs function Ahlchu function Abnlokdw functionj |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter A= in cell C11. @@@@@@@Enter B= in cell C12. @@@@@@@Enter =COMPLEX(5,-3) in half-width in cell D11. @@@@@@@Enter =COMPLEX(-2,7) in half-width in cell D12. @@@@@@@Enter C= in half-width in cell F11. @@@@@@@Enter D= in half-width in cell F12. @@@@@@@Enter =COMPLEX(2,1) in half-width in cell G11. @@@@@@@Enter =COMPLEX(2,-1) in half-width in cell G12. @@@@@@@Enter data in the cell range B14:B17 as shown in the table above. @@@@@@@Enter data in the cell range C14:C17 as shown in the table above. @@@@@@@Enter =IMSUM(D11,D12) in half-width in cell D14. @@@@@@@Enter =IMSUB(D11,D12) in half-width in cell D15. @@@@@@@Enter =IMPRODUCT(D11,D12) in half-width in cell D16. @@@@@@@Enter =IMDIV(G11,G12) in half-width in cell D17. @@@About functions @@@@@@@hlrtl function¥¥¥ IMSUM(complex number 1Ccomplex number 2) @@@@@@@@@@Returns the value of (complex number 1 + complex number 2) @@@@@@@hlrta function¥¥¥ IMSUB(complex number 1Ccomplex number 2) @@@@@@@@@@Returns the value of (comlex number 1 - complex number 2) @@@@@@@hloqnctbs function¥¥¥ IMPRODUCT(comlex number 1Ccomplex number 2) @@@@@@@@@@Returns the value of (comlex number 1 ~ complex number 2) @@@@@@@hlchu function¥¥¥ IMDIV(comlex number 1Ccomplex number 2) @@@@@@@@@@Returns the value of (comlex number 1 complex number 2) @@@@@@@bnlokdw function¥¥¥ COMPLEX(real number 1Creal number 2) @@@@@@@@@@Returns the complex number form (real number 1) + (real number 2) i |
| @y1004zConjugate complex number and Abloluete values @@@@@@ihlbnmitf`sd functionAhl`ar functionj |
||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to compleete the worksheet abovet @@@@@@@Enter 3+4i in half-width in cell B12. @@@@@@@Enter 3 in half-width in cell B13. @@@@@@@Enter 3i in half-width in cell B14. @@@@@@@Enter =IMCONJUGATE(B12) in half-width in cell C12. @@@@@@@Enter =IMCONJUGATE(B13) in half-width in cell C13. @@@@@@@Enter =IMCONJUGATE(B14) in half-width in cell C14. @@@@@@@Enter =IMABS(B12) in half-width in cell D12. @@@@@@@Enter =IMABS(B13) in half-width in cell D13. @@@@@@@Enter =IMABS(B14) in half-width in cell D14. @@@About functions @@@@@@@hlbnmitf`sd function¥¥¥ IMCONJUGATE(complex number 1) @@@@@@@@@@Returns complex number that is the conjugate of complex number 1. @@@@@@@hl`ar function¥¥¥ IMABS(complex number 1) @@@@@@@@@@Returns the absolute value of a complex number 1. @ |
| @y1005zargument , real part , imaginary part of complex number @@@@@@ihl`qftldms functionAhlqd`k functionAhl`fhm`qx functionj |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Drag the cell range B11:B20 , right-click and select Cell formatting. @@@@@@@Select Display format ¨ Classification string ¨ OK @@@@@@@Enter data in the ccll range B11:B20 as shown in the table above. @@@@@@@Enter =COMPLEX(1,0) in half-width in cell C12. @@@@@@@Enter =COMPLEX(SQRT(3),1) in half-width in cell C13. @@@@@@@Enter =COMPLEX(1,1) in half-width in cell C14. @@@@@@@Enter =COMPLEX(1,SQRT(3)) in half-width in cell C15. @@@@@@@Enter =COMPLEX(0,1) in half-width in cell C16. @@@@@@@Enter =COMPLEX(-1,SQRT(3)) in half-width in cell C17. @@@@@@@Enter =COMPLEX(SQRT(-1,1) in half-width in cell C18. @@@@@@@Enter =COMPLEX(-SQRT(3),1) in half-width in cell C19. @@@@@@@Enter =COMPLEX(-1,0) in half-width in cell C20. @@@@@@@Enter =DEGREES(IMARGUMENT(C12)) in half-width in cell D12. @@@@@@@Right-click on the cell D12 and select Copy. @@@@@@@Drag the cell range D13:D20 , right-click and select Paste. @@@@@@@Enter =IMREAL(C12) in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy. @@@@@@@Drag the cell range E13:E20 , right-click and select Paste. @@@@@@@Enter =IMAGINARY(C12) in half-width in cell F12. @@@@@@@Right-click on the cell F12 and select Copy. @@@@@@@Drag the cell range F13:F20 , right-click and select Paste. @@@About functions @@@@@@@hl`qftldms function¥¥¥ IMARGUMENT(complex number 1) @@@@@@@@@@Returns the argument of a complex number 1 in radians. unit @@@@@@@hlqd`k function¥¥¥ IMREAL(complex number 1) @@@@@@@@@@Returns the real part of a complex number 1. @@@@@@@hl`fhm`qx function¥¥¥ IMAGINARY(complex number 1) @@@@@@@@@@Returns the imaginary part of a complex number 1. |
| @y1006zThink of @@@@@@@@@@de Moivle's theorem @@@@@@@@@@@@ @@@@@@@@@@@@ihlonvdq functionj |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet. @@@Reference @@@@@Refer to y401z how to complete the worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range B9:B23 as shown in the table above. @@@@@@@Enter =COMPLEX(1,SQRT(3)) in half-width in cell C9. @@@@@@@Enter data in the cell C11 as shown in the table above. @@@@@@@Enter =IMPOWER($C$9,B12) in half-width in cell C12. @@@@@@@Right-click on the cell C12 and select Copy. @@@@@@@Drag the cell range C13:C23 , right-click and select Paste. @@@@@@@Enter =DEGREES(IMAGUMENT(C12)) in half-width in cell D12. @@@@@@@Right-click on the cell D12 and select Copy. @@@@@@@Drag the cell range D13:D23 , right-click and select Paste. @@@@@@@Enter =IMABS(C12) in half-width in cell E12. @@@@@@@Right-click on the cell E12 and select Copy. @@@@@@@Drag the cell range E13:E23 , right-click and select Paste. @@@About functions @@@@@@@hlonvdq function¥¥¥ IMPOWER(complex number 1C) @@@@@@@@@@Returns (complex number 1)^n. |
| @y1007z@When the points represented by ¿,À, and Áare A , B ,and C respectively , find the magnitude of Ú`ab.@@@@@@@ | ||||||||||||||||||||||||||||||||||||
| @Procedure @@@@@@@@@@For points `(¿)Aa(À)Aand b(Á) @@@@@@@@@@ @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range B11:B18 as shown in the table above. @@@@@@@Enter =COMPLEX(1+SQRT(3),-2+SQRT(3)) in half-width in cell C11. @@@@@@@Enter =COMPLEX(0,-1) in half-width in cell C12. @@@@@@@Enter =COMPLEX(1,-2) in half-width in cell C13. @@@@@@@Enter =IMSUB(C11,C13) in half-width in cell C15. @@@@@@@Enter =IMSUB(C12,C13) in half-width in cell C16. @@@@@@@Enter data in the cell C18 as shown in the table above. @@@@@@@Enter =DEGREES(IMARGUMENT(IMDIV(C16,C15))) in half-width in cell D18. @@@Consideration @@@@@@@ @@@@@@@À|Á||(P|Q)|P{ @@@@@@@Calculate and find arg{(À|Á)/(¿|Á)}. |
| @To table of contents@ |
| @y1101z@When the integer part of ã5 is a and the decimal part of ã5 is b , find the value of (a^2-b^2). | |||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet above.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range B11:B16 as shown in the table above. @@@@@@@Enter =TRUNC(SQRT(5)) in half-width in cell C11. @@@@@@@Enter =SQRT(5)-C11 in half-width in cell C12. @@@@@@@Enter =POWER(C11,2)-POWER(C12,2) in half-width in cell C14. @@@@@@@Enter =4*SQRT(5)-5 in half-width in cell C16. @@@About functions @@@@@@@onvdq function¥¥¥ POWER(real number 1C) @@@@@@@@@@Returns (real number 1)^n @@@@@@@sqtmb function¥¥¥ TRUNC(real number 1) @@@@@@@@@@Returns a real number 1 with the decimal part truncated. @@@Consideration @@@@@@@Since a=2 , b=ã5 - 2 @@@@@@@ @@@@@@Make sure that the value of a^2-b^2 on the worksheet matches the value of 4ã5 - 5. @ |
| @y1102z@Find the value of a^2+8a when the decimal part of ã23 is a. | |||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range B11:B14 as shown in the table above. @@@@@@@Enter =TRUNC(SQRT(23)) in half-width in cell C11. @@@@@@@Enter =SQRT(23)-C11 in half-width in cell C12. @@@@@@@Enter =POWER(C12,2)+8*C12 in half-width in cell C14. @@@About functions @@@@@@@onvdq function¥¥¥ POWER(real number 1Cn) @@@@@@@@@@Returns (real nimber 1)^n @@@@@@@sqtmb function ¥¥¥ TRUNC(real number 1) @@@@@@@@@@Returns a real number 1 with the decimal part truncated. @@@Consideration @@@@@@@Since a=ãQR@|@S @@@@@@@ @@@@@@@Make sure that this matches the value of a^2+8a on the worksheet. @ |
| @To table of contens@ |
| @y1201z@Regarding the tangent at point (t , t^3+t^2-2t) on the cubic function y=x^3+x^2-2x , observe the state of the tangent when t moves within the range of -2.8 to 2.1. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range A2:A62 in increments of 0.1 as shown in the table above. @@@@@@@Enter A2^3+A2^2-2*A2 in half-width in cell B2. @@@@@@@Copy cell B2 to the cell range B3:B62. @@@@@@@Enter (3*$F$2^2+2*$F$2-2)*A2-2*$F$2^3-$F$2^2 in half-width in cell C2. @@@@@@@Copy cell C2 to the cell range C3:C62. @@@@@@@Enter F2^3+F2^2-2*F2 in half-width in cell G2. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range A1:C62 in the correspondence table of (1) above. @@@@@@A Left-click mInsertn¨mScatter plotn¨mScatter linen @@@@@@B Delete the legend @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Set the x-axis scale to -3 or more and 3 or less , and set the scale interval to 1. @@@@@@A Set the y-axis scale to -10 or more and 10 or less , and set the scale interval to 1 @@@@@@B Set the scale line style to dotted lines for both the x-axis and y-axis. 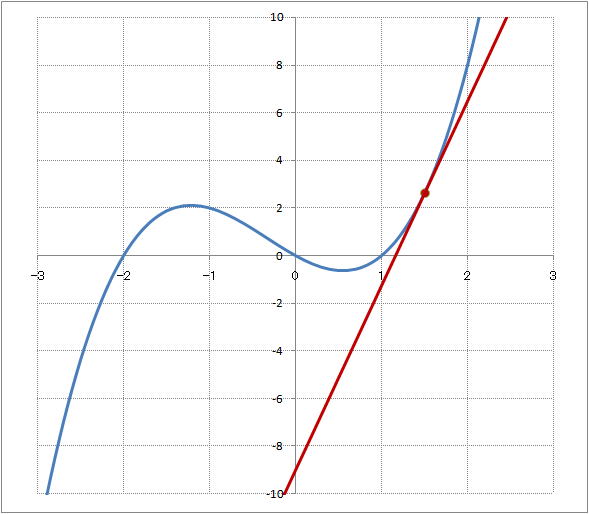 @@@About Macro @@@@@@@ @@@@@Sub Sessen() @@@@@@@@Dim t As Single @@@@@ @'Declare it as single-precision floating point type @@@@@@@@DoEvents @@@@@@@@@@ 'Allow you to force exit from ForNext repetition. @@@@@@@@For t = -2.8 To 2.1 Step 0.01 @@@@@@@@@@@Cells(2, "F") = t @@@'Assign the the value of t to row 2 and column F. @@@@@@@@@@@Calculate @@@@@@@ 'Recalculate @@@@@@@@Next @@@@@End Sub @@@Consideration @@@@@@@Let's run the macro and observe the movement of the tangent line. @@@@@@@You can observe the state of the tangent line as the x-coordinate of the contact point changes from -2.8 to 2.1. @ |
| @y1202z@Observe that the graph of the quadratic function y=a(x-p)^2+q is obtained by translaing the graph of y=ax^2 by +p in the x-axis direction and +q in the y-axis direction. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range B3:B63 in increments of 0.1 as shown in the table above. @@@@@@@Enter $G$2*(B3-$G$3)^2+$G$4 in half-width in cell C3 @@@@@@@Copy the cell C3 to the cell range C4:C63. @@@@@@@Enter $G$2*(B3-$I$8)^2+$J$8 in half-width in cell D3. @@@@@@@Copy the cell D3 to the cell range D4:D63. @@@@@@@Enter =I8 in half-width in cell I7. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range B2:D63 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mScatter linen @@@@@@B Delete the legend. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Set the x-axis scale to -3 or more and 3 or less , and set the scale interval to 1. @@@@@@A Set the y-axis scale to -10 or more and 10 or less , and set the scale interval to 1. @@@@@@B Set the scale line style to dotted lines for the x-axis and y-axis. 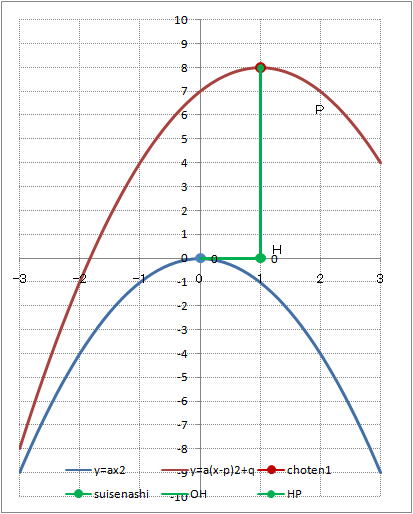 @@@@@ @@@@@ @@@About macro @@@@@@@ @@@Option Explicit@@@@@'Force bariable declaration @@@Sub apq() @@@@@@@Dim a, p, q As Single@@@@@'Declare as simple-precision floating point type @@@@@@@Dim sp, sq As Single@@@@@'Declare as simple-precision floating point type @@@@@@@sp = Cells(8, "I")@@@@@'Assign the value of row 8 and column I to sp @@@@@@@sq = Cells(8, "J")@@@@@'Assign the value of row 8 and column J to sq @@@@@@@Cells(3, "G") = 0@@@@@'Write 0 in row 3 and couimn G @@@@@@@Cells(4, "G") = 0@@@@@'Write 0 in row 4 and column G @@@@@@@DoEvents@@@@@'Allow forcible exit from ForNext statement @@@@@@@If sp > 0 And sq > 0 Then@@@@@'If the vertex is in the first quadrant @@@@@@@@@@Cells(3, "G") = 0@@@@@'Write 0 in row 3 and column G @@@@@@@@@@Cells(4, "G") = 0@@@@@'Write 0 in row 4 and column G @@@@@@@@@@For p = 0 To sp Step 0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'Write the value of p in row 3 and column G @@@@@@@@@@@@@Calculate@@@@@'Recaluculate @@@@@@@@@@Next@p @@@@@@@@@@For q = 0 To sq Step 0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'Write the value of q in row 4 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next@q @@@@@@@End If @@@@@@@If sp > 0 And sq < 0 Then@@@@@'If the vertex is in the 4th quadrant @@@@@@@@@@Cells(3, "G") = 0@@@@@'Write 0 in row 3 and column G @@@@@@@@@@Cells(4, "G") = 0@@@@@'Write 0 in row 4 and column G @@@@@@@@@@For p = 0 To sp Step 0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'Write the value of p in row 3 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next p @@@@@@@@@@For q = 0 To sq Step -0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'Write the value of q in row 4 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next q @@@@@@@End If @@@@@@@If sp < 0 And sq > 0 Then@@@@@'If the vertex is in the 2nd quadrant @@@@@@@@@@Cells(3, "G") = 0@@@@@'Write 0 in row 3 and column G @@@@@@@@@@Cells(4, "G") = 0@@@@@'Write 0 in row 4 and column G @@@@@@@@@@For p = 0 To sp Step -0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'Write the value of p in row 3 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next p @@@@@@@@@@For q = 0 To sq Step 0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'Write the value of q in row 4 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next q @@@@@@@End If @@@@@@@If sp < 0 And sq < 0 Then@@@@@''If the vertex is in the 3rd quadrant @@@@@@@@@@Cells(3, "G") = 0@@@@@'Write 0 in row 3 and column G @@@@@@@@@@Cells(4, "G") = 0@@@@@'Write 0 in row 4 and column G @@@@@@@@@@For p = 0 To sp Step -0.05 @@@@@@@@@@@@@Cells(3, "G") = p@@@@@'Write the value of p in row 3 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next p @@@@@@@@@@For q = 0 To sq Step -0.05 @@@@@@@@@@@@@Cells(4, "G") = q@@@@@'Write the value of q in row 4 and column G @@@@@@@@@@@@@Calculate@@@@@'Recalculate @@@@@@@@@@Next q @@@@@@@End If @@@End Sub @@@Consideration @@@@@@@Let's run the macro and observe that the quadratic function y=a(x-p)^2+q is obtained by translating y=ax^2 by +p in the x-axis direction and +q in the y-axis direction. @ |
| @To table of contents@ |
| @y1301z Find prime numbers less than or equal to 20 using a macro.@@@@@@@@@@@ |
@@@About prime number @@@@@@@A prime number is a natural number greater than or equal to 2 that has no positive divisors other than 1 and itself. @@@@@@@The following macro determines whether a number is prime by dividing it one by one until 2 or more and 1 smaller than itself and checking whether it is divisible. @@@About macro @@@@@@@ @@@Sub Sosu2() @@@@@@For n = 2 To 20 @@@@@@@@@d = 0 @@@@@'Initialize d @@@@@@@@@For k = 2 To n - 1 @@@@@@@@@@@@If n Mod k = 0 Then @@@@@'If k is a divisor of n @@@@@@@@@@@@@@@d = d + 1@@@@@ 'Add 1 to d. @@@@@@@@@@@@End If @@@@@@@@@Next k @@@@@@@@@If d = 0 Then @@@@@'If d=0 @@@@@@@@@@@@MsgBox (n & "is primeI") @@@@@'Display the message that d is a prime number. @@@@@@@@@End If @@@@@@Next n @@@@@@MsgBox ((n - 1) & " We have now completed our search for the following prime numbers.") @'Display the "End" message. @@@End Sub @@@Consideration @@@@@@@Let's run the macro and find prime numbers less than or equal to 20. @@@@@@@Next , let's rewrite the macro and find prime numbers less than or equal to 30. @ |
| @y1302z@Find perfect numbers using a method other than brute force.@ | ||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@@@@@¦ Follow the steps below so that column D does not display "¥¥¥¥¥E-12". @@@@@@@@@Select column D ¨ Right+click ¨ Format cells ¨ Display format ¨ Numerical value ¨ nj @@@About perfect number @@@@@@@A perfect number is a natural number whose sum of positive divisors , excluding itself , is equal to itself. For example , the divisors of 6 , excluding itself , are 1,2,3 , so 1+2+3=6 , thefore , 6 is a perfect number. @@@@@@When n is a natural number greater than or equal to 2 and @@@@@@So , are all perfect numbers expressed as @@@@@@It has been proven that all even perfect numbers are denoted by @@@@@@However , the odd perfect number has not yet been discovered. It has not been proven that the odd perfect numbers don't exist. @@@@@@The following macro uses the fact that "When n is a natural number greater than or equal to 2 and @@@About macro @@@Sub Kanzensusp() @@@@@@Dim n As Long @@@@@'Declare as long integer type @@@@@@Dim k As Long @@@@@'Declare as long integer type @@@@@@Dim d As Long @@@@@'Declare as long integer type @@@@@@'Cells.Clear @@@@@@DoEvents @@@@@'Make it possible to stop even in the middle of a ForLoop @@@@@@For n = 2 To 31 @@@@@@@@@Cells(n, "A") = n @@@'Assign the value of n to row n and column A @@@@@@@@@Cells(n, "B") = 2 ^ n - 1@@@ 'Assign the value of 2^n-1 to row n and column B. @@@@@@@@@d = 0@@@@@ 'initialize d. @@@@@@@@@For k = 2 To 2 ^ n - 1 - 1 @@@@@@@@@@@@If (2 ^ n - 1) Mod k = 0 Then @@@'If k is a divisor of 2^n-1 , then @@@@@@@@@@@@@@@d = d + 1@@@ 'Add 1 to d @@@@@@@@@@@@End If @@@@@@@@@Next k @@@@@@@@@If d = 0 Then @@@@@'If d=0 then , then @@@@@@@@@@@@Cells(n, "C") = "Prime" @@@'Assign "Prime number " to row n and column C. @@@@@@@@@End If @@@@@@@@@Cells(n, "D") = (2 ^ (n - 1)) * (2 ^ n - 1) 'Assign the value of 2^(n-1)*(2^n-1) to row n and column D @@@@@@@@@If Cells(n, "C") = "Prime" Then @@@@@'If row n and column C is "Prime number" , then @@@@@@@@@@@@Cells(n, "E") = "Perfect" @@@@@'Assign "Perfect number" to row n and column E @@@@@@@@@End If @@@@@@Next n @@@@@@MsgBox ("The search of perfect numbers has ended...") 'Display a completion message. @@@End Sub @@@Consideration @@@@@@ Let's run the macro and find the perfect numbers. @@@@@@ It will take some time to find 8 perfect numbers. @ |
| @To table of contents@ |
| @y1401z@Draw a figure (positive leaf curve) repesented by the polar equetion Æ. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a warksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@ Enter data in the cell range A2:A362 in 1 complements as shown in the the table above. @@@@@@ Enter SIN($F$2*RADIANS(A2)) in half-width in cell B2. @@@@@@ Copy cell B2 to the cell range B3:B362. @@@@@@ Enter B2*COS(RADIANS(A2)) in half-width in cell C21. @@@@@@ Copy cell C2 to cell range C3:D362. @@@@@@ Enter B2*SIN(RADIANS(A2)) in half-width in cell D2. @@@@@@ Copy cell D2 to the cell range D3:D362. @@@@@@ Enter "a=" in cell E2. @@@@@@ Enter "2" in cell F2. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range C2:D362 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mScatter plot (smooth line)n @@@@@@B Delete the legend. @@@(3) Arrange the xy coordinate plane on which the graph is drawn. @@@@@@@ Set the scale interval of the x-axis to 0.1 between -1 and 1. @@@@@@A Set the scale interval of the y-axis to 0.1 between -1 and 1. @@@@@@B Set the scale line style to dotted lines for both the x-axis and y-axis. 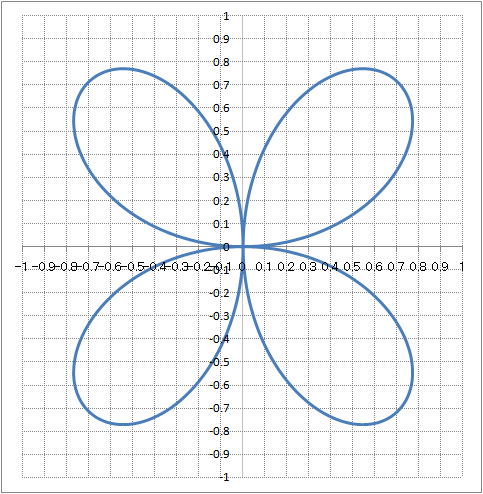 @@@@@@@q`ch`mr function ¥¥¥ q`ch`mr(Angle in degrees) @@@@@@@@@@Convert an angle in degrees to arc degrees. @@@About macro @@@@@@@Sub Seiyou() @@@@@@@@@@Dim a As Single@@@'Declare a as a single-precision floating point type. @@@@@@@@@@For a = 0 To 10.05 Step 0.05 @@@@@@@@@@@@@Cells(2, "F") = a@@@'Assign the value of a to row 2 and column F. @@@@@@@@@@@@@Calculate@@@'Recalculate @@@@@@@@@@Next a @@@@@@@End Sub @@@Consideration @@@@@@@Let's sequentially substitute 2 , 3 , 4 , ¥¥¥,10 into cell F2 (value of a) and observe the drawn figure (positive leaf curve). @@@@@@@Also , let's run the macro and observe the figures drawn as the value of a changes from 0 to 10 in 0.05 increments. @ |
| @y1402z@Draw the figure (Archimedes spiral line) represented by the polar equation r=aÆ. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @Procedure @@@(1) Create the following correspondence table on a worksheet.
@@@Reference @@@@@sHow to complete the worksheet abovet @@@@@@@Enter data in the cell range A2:A722 in increments of 1 as shown in the table above. @@@@@@@Enter $F$2*RADIANS(A2) in half-width in cell B2. @@@@@@@Copy cell B2 to the cell range B3:B722. @@@@@@ Enter B2*COS(RADIANS(A2)) in half-width in cell C2. @@@@@@@Copy cell C2 to the cell range C3:C722. @@@@@@ Enter B2*SIN(RADIANS(A2)) in half-width in cell D2. @@@@@@@Copy cell D2 to the cell range D3:D722. @@@@@@@Enter "a=" in cell E2. @@@@@@@Enter "2" in cell F2. @@@(2) Draw a graph from the correspondence table in (1) above. @@@@@@@ Drag and select the cell range C2:D722 in the correspondence table of (1) above. @@@@@@A Left-click mIncertn¨mScatter plotn¨mScatter plotiSmooth linejn @@@@@@B Delete legend. @@@(3) Arrange the xy-coordinate plane on which the graph is drawn. @@@@@@@ Set the x-axis scale to -150 or more and 150 or less , and set the scale interval to 30. @@@@@@A Set the y-axis scale to -150 or more and 150 or less , and set the scale interval to 30. @@@@@@B Set the scale line style to the dotted lines for both the x-axis and y-axis. 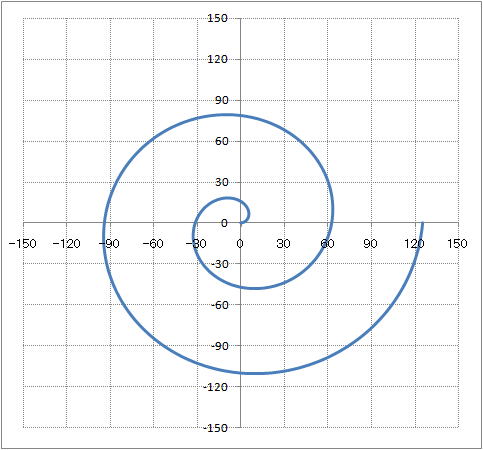 @@@About functions @@@@@@@q`ch`mr function¥¥¥ q`ch`mr(Angle in degrees) @@@@@@@@@@Convert angles in degrees to arc degrees. @@@About macro @@@@@@@Sub Aruki() @@@@@@@@@@Dim a As Single@@@'Declare a as a singe-precision floating point type @@@@@@@@@@For a = 0 To 10.05 Step 0.05 @@@@@@@@@@@@@Cells(2, "F") = a@@@'Assign the value of a to row 2 and column F. @@@@@@@@@@@@@Calculate@@@'Recalculate @@@@@@@@@@Next a @@@@@@@End Sub @@@Consideration @@@@@@@Let's sequentially assign 2 , 3 , 4 , ¥¥¥, 10 to cell F2 (value of a) and obseve the drawn figure (Archmedean spiral line). @@@@@@@Also , let's run the macro and observe the figures drawn as the value of a changes from 0 to 10 in 0.05 increments. @ |
| ¦@You can download the above sample data files "`.xls" below. |
| @To table contents@ |
| @When you downloaded the data below for how to use Excel , compressed file
"sample_excel.lzh" will be downloaded. @When the downloaded compressed file "sample_excel.lzh" is decompressed , a folder "Sample data for thinking about how to use "Excel" is created. @When you download the sample data for "simulation" , "Prime and Perfect Numbers" , and "Polar Equation"below , copmressed file "ExcelSample2.lzh" will be downloaded. @When the downloaded compressed file "ExcelSample2.lzh" is downloaded , the sample data "Simulation" , "Prime and Perfect Number" , and "Polor Equation" are created. |
| @d sample data | @Sample data for thinking about how to use "Excel" |
| @d sample data 2@ | @"Simulation" , "Prime and Perfect Number" , "Polar Equation "sample data |
| @To table of contents@ |
| @There are 11 folders "[0100]Quadratic function" , "[0200]Trigonometric function" , "[0300]Exponential function" , "[0400]Logarithmic function" , "[0500]Various curves" , "[0600]Differentiation(Part 1)" , "[0700]Differentiation (Part 2)" , "[0800]Integral" , "[0900]Number sequence" , "[1000]Complex number" , "[1100]Application of square roots" in the folder "Sample data for thinking about how to use Excel". Open the files "`.xlsm" in each folder in Excel. |
| @There are six files in the folder "Simulation " , "Prime and Perfect Numbers" , "Polor Equations" sample data. Open each file "`.xlsm" in Excel. |