 |

 |

| LastUpdate 2023/3/30 |
| 私とコンピュータとの出会いは大学の講義のときでした。フォートランというプログラム言語の書き方の講義で、紙テープに穴を開けて、大きなコンピュータに作成したプログラムを読ませた記憶があります。 教員1年目の勤務校で出会ったのが「NEC-PC9801」というパソコンでした。記録媒体として、今から思うとかなり大きな5インチフロッピーディスクを本体に差し込むようになっていました。 因みに、私が家で使うために購入したパソコンの記録媒体はカセットテープでした。パソコン専用のカセットテープではなく、音楽を聴いたり記憶したりするための現在でもあるカセットテープレコーダー用のカセットテープでした。起動用のプログラムもこのカセットテープに入っていて、コンピュータが立ち上がる(スイッチを入れて使えるようになる)までに5分ぐらいかかったことを覚えています。 当時、コンピュータは数値計算をする機械であり、数式の計算はできませんでした。しかし、今ではコンピュータが数値だけでなく、数式も計算してしまうようになりました。数式処理ソフトを使えば、「式の整理」、「展開」、「因数分解」、「1次方程式の解法」、「2次方程式の解法」、「3次方程式の解法」、「4次方程式の解法」、「微分」、「積分」などはお茶の子さいさいです。 「Maxima」を用いると、3次元のグラフも簡単に描くことができ、グラフをドラッグすることでグラフを見る方向を自由に変えることができます。 数式処理ソフトの代表的なものには、①「Mathematica」 ②「Maple」 ③「Maxima」 などがあります。①、②が20万円から30万円と高額であるのに対して、③「Maxima」は完全なフリーソフトなので無料です。 また、「Maxima」のソースコードは公開されていて(オープンソース)、世界中のありとあらゆる人がボランティアで開発に参加しています。「Maxima」はLispというプログラム言語で書かれています。 なお、以下の例には『wxMaxima 0.8.7』 を使用しました。 |
| No | 目 次 |
| 1 | 3次元陽関数のグラフ (その1) |
| 2 | 3次元陰関数のグラフ (その1) |
| 3 | 3次元媒介変数のグラフ (その1) |
| 4 | 2次元陽関数のグラフ (その1) |
| 5 | 2次元陰関数のグラフ (その1) |
| 6 | 2次元媒介変数のグラフ (その1) |
| 7 | 3次元陰関数のグラフ(その2) |
| 8 | 2次元陽関数のグラフ (その2) |
| 9 | 2次元媒介変数のグラフ (その2) |
| 10 | 3次元陽関数のグラフ (その2) |
| 11 | 3次元媒介変数のグラフ (その2) |
| 12 | 2次元陽関数のグラフ (その3) |
| 13 | 2次元媒介変数のグラフ (その3) |
| 14 | 3次元陽関数のグラフ (その3) |
| 15 | 3次元媒介変数のグラフ (その3) |
| 16 | 回転体 |
| 17 | テーラー展開による式の近似 |
| 18 | オイラーの公式の証明 |
| 19 | その他 |
| 20 | ダウンロードとインストール |
| 21 | 『Maxima』の実行 |
| 22 | サンプルデータについて |
| 【例 1】 3次元陽関数のグラフを描く。[メキシカンハット] |
[1]関数式 [2]入力式 plot3d(sin(sqrt(x^2+y^2))/sqrt(x^2+y^2),[x,-3*%pi,3*%pi],[y,-3*%pi,3*%pi],[plot_format,gnuplot],[grid,50,50]); [3]描写結果 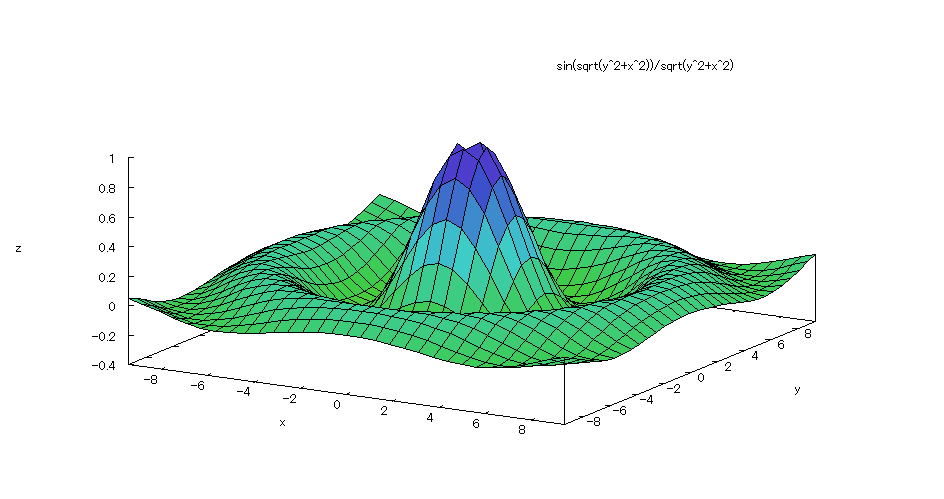 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 2】 3次元陽関数のグラフを描く。[カルデラの形] |
[1]関数式 [2]入力式 plot3d(exp(-(x^2+y^2)/2)*(x^2+y^2)/(2*%pi),[x,-2,2],[y,-2,2],[plot_format,gnuplot],[grid,50,50]); [3]描写結果 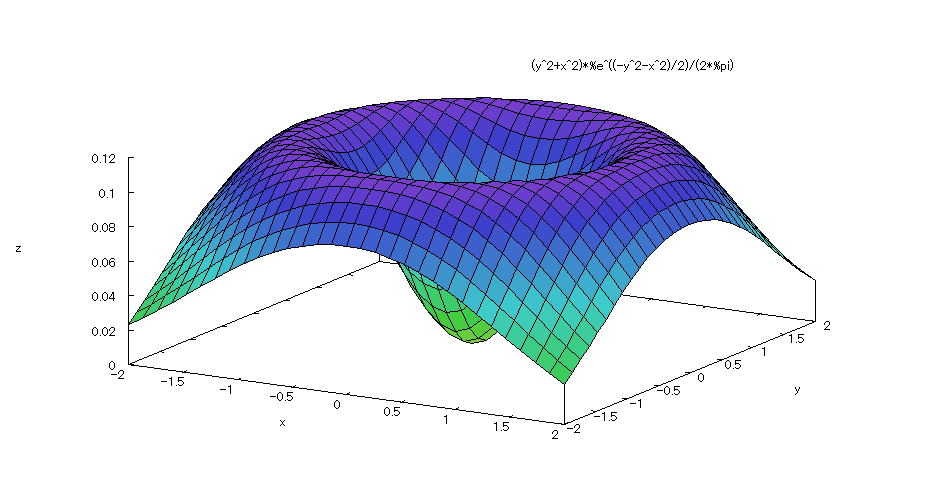 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 3】 3次元陽関数のグラフを描く。[少し陥没した鞍の形] |
[1]関数式 [2]入力式 plot3d(3*exp(-(x^2+y^2))*(2*x^2+y^2),[x,-2,2],[y,-2,2],[plot_format,gnuplot],[grid,50,50]); [3]描写結果 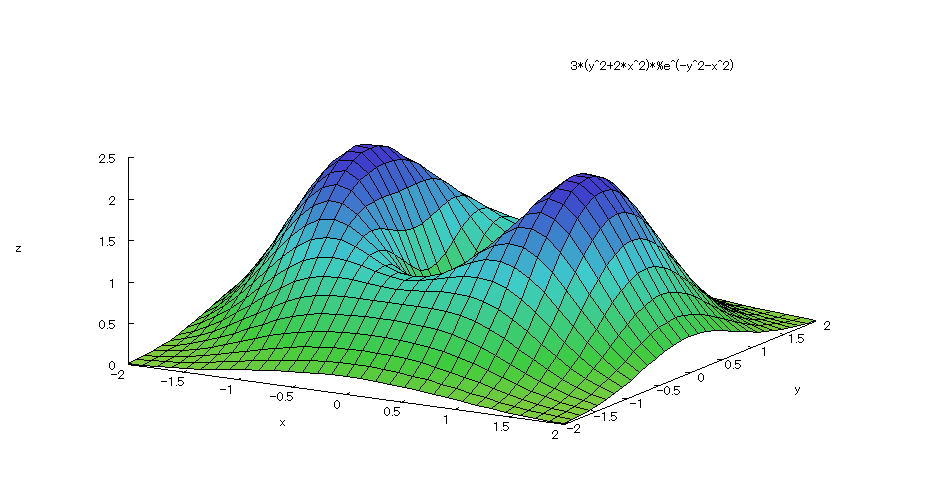 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 4】 3次元陰関数のグラフをワイヤーフレームで描く。[球] |
[1]関数式 [2]入力式 draw3d(implicit(x^2+y^2+z^2=1,x,-1,1,y,-1,1,z,-1,1)); [3]描写結果 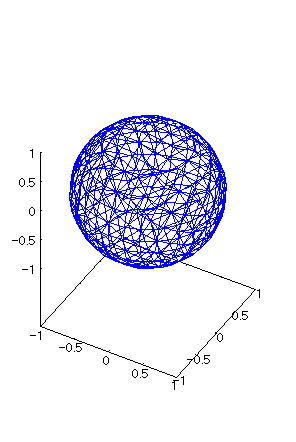 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 5】 3次元陰関数のグラフを陰面処理で描く。[球] |
[1]関数式 [2]入力式 draw3d(enhanced3d=true,implicit(x^2+y^2+z^2=1,x,-1,1,y,-1,1,z,-1,1)); [3]描写結果 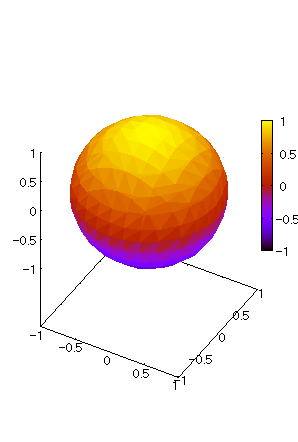 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 6】 3次元陰関数のグラフを陰面処理で描く。[中空き鼓] |
[1]関数式 [2]入力式 draw3d(enhanced3d=true,implicit(x^2+y^2-z^2=1,x,-2,2,y,-2,2,z,-2,2)); [3]描写結果 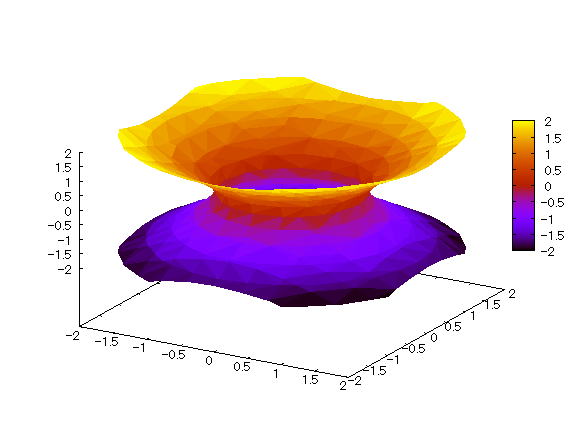 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 7】 3次元陰関数のグラフを陰面処理で描く。[下水管継ぎ目] |
[1]関数式 [2]入力式 draw3d(enhanced3d=true,implicit((x^2-1)^2+(y^2-1)^2+(z^2-1)^2=1.5, x,-1,1,y,-1,1,z,-1,1)); [3]描写結果 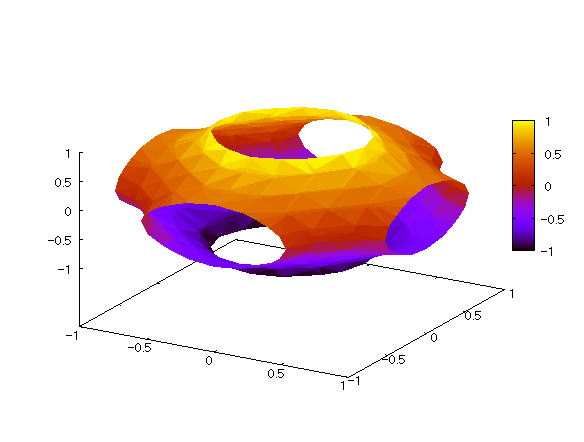 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 8】 3次元陰関数のグラフを陰面処理で描く。[中心に核をもつ細胞] |
[1]関数式 cos(x+φy)+cos(x-φy) +cos(y+φz)+cos(y-φz)+cos(z+φx)+cos(z-φx)=2 (ただし、φは黄金比を表す) [2]入力式 draw3d(enhanced3d=true,implicit(cos(x+%phi*y)+cos(x-%phi*y)+cos(y+%phi*z) +cos(y-%phi*z)+cos(z+%phi*x)+cos(z-%phi*x)=2,x,-4,4,y,-4,4,z,-4,4)); [3]描写結果 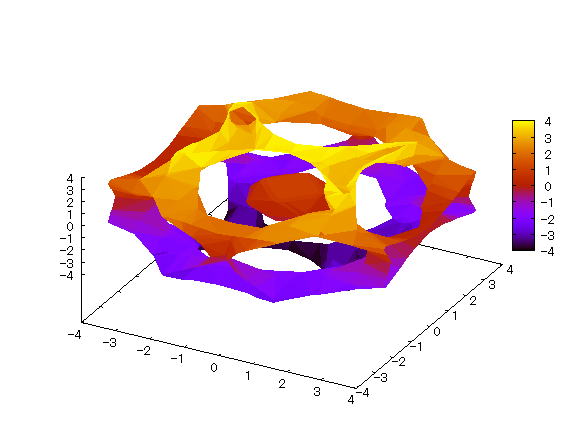 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 9】 3次元媒介変数のグラフを描く。[球] |
[1]関数式 x=coss・cost y=coss・sint z=sins (0≦s≦2π) (0≦t≦π) [2]入力式 plot3d([cos(s)*cos(t),cos(s)*sin(t),sin(s)],[s,0,2*%pi],[t,0,%pi]); [3]描写結果 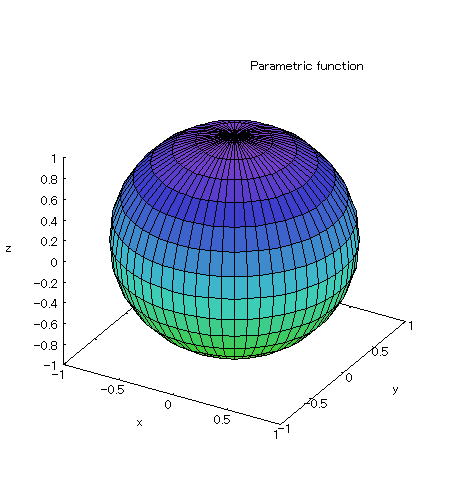 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 10】 3次元媒介変数のグラフを描く。[ドーナツ型(トーラス)] |
[1]関数式 x=(5+2coss)cost y=(5+2coss)sint z=2sins (0≦s≦2π) (0≦t≦2π) [2]入力式 plot3d([(5+2*cos(s))*cos(t),(5+2*cos(s))*sin(t),2*sin(s)],[s,0,2*%pi],[t,0,2*%pi]); [3]描写結果 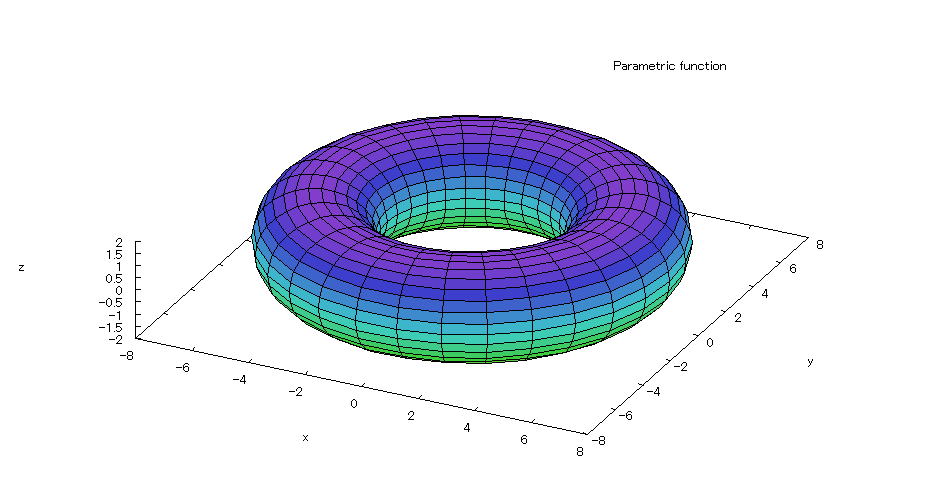 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 11】 3次元媒介変数のグラフを描く。[バネ型] |
[1]関数式 x=(5+coss)cost y=(5+coss)sint z=sins+0.6t (0≦s≦2π) (0≦t≦7π) [2]入力式 plot3d([(5+cos(s))*cos(t),(5+cos(s))*sin(t),sin(s)+0.6*t],[s,0,2*%pi],[t,0,7*%pi]); [3]描写結果 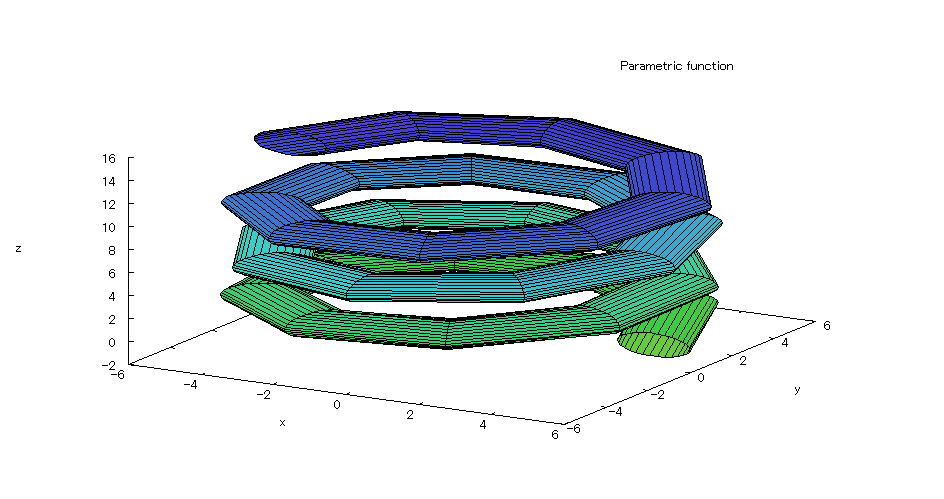 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 12】 3次元媒介変数のグラフを描く。[メビウスの帯] |
[1]関数式 [2]入力式 plot3d([cos(s)*(3+t*cos(s/2)),sin(s)*(3+t*cos(s/2)),t*sin(s/2)],[s,0-%pi,%pi],[t,-1,1]); [3]描写結果 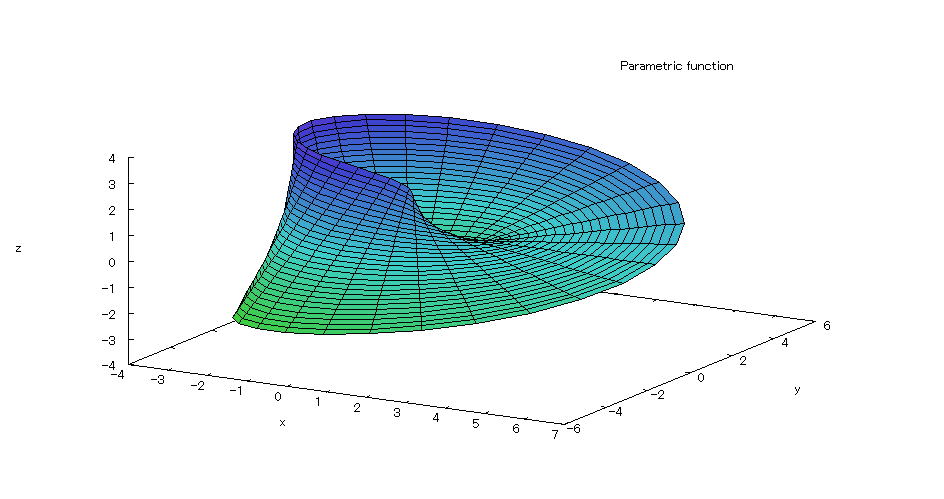 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 13】 3次元媒介変数のグラフを描く。[クラインの壺] |
[1]関数式 (-π≦s≦π) (-π≦t≦π) [2]入力式 plot3d([5*cos(s)*(cos(s/2)*cos(t)+sin(s/2)*sin(2*t)+3)-10, -5*sin(s)*(cos(s/2)*cos(t)+sin(s/2)*sin(2*t)+3.0),5*(-sin(s/2)*cos(t)+cos(s/2)*sin(2*t))], [s,-%pi,%pi],[t,-%pi,%pi]); [3]描写結果 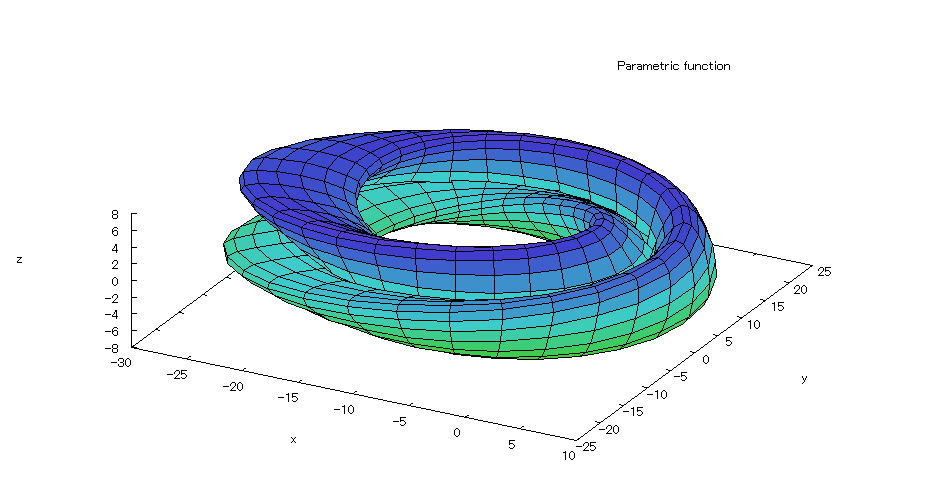 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 14】 2次元陽関数のグラフを描く。[2次関数] |
[1]関数式 [2]入力式 plot2d(3*x^2-1,[x,-2,2]); [3]描写結果 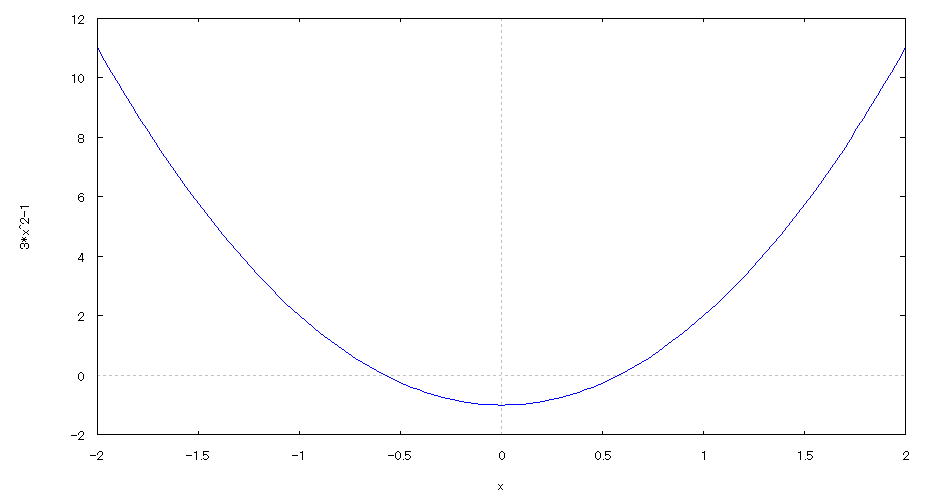 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 15】 2次元陽関数のグラフを描く。[指数関数・三角関数] |
[1]関数式 [2]入力式 plot2d(exp(x)*sin(7*x),[x,0,20]); [3]描写結果 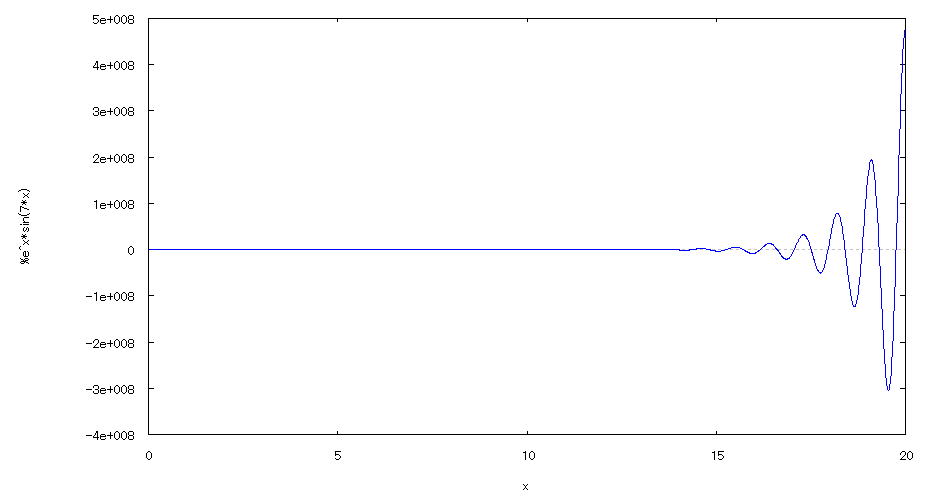 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 16】 2次元陽関数のグラフを描く。[複数のグラフを同時に描写] |
[1]関数式 y=sinx、y=sin2x、y=sin3x (0≦x≦2π) [2]入力式 plot2d([sin(x),sin(2*x),sin(3*x)],[x,0,2*%pi]); [3]描写結果 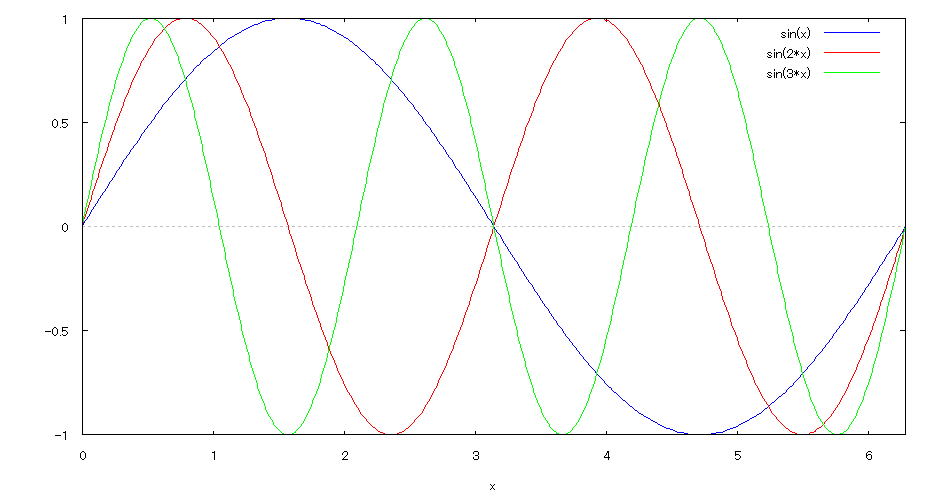 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 17】 2次元陰関数のグラフを描く。[円] |
[1]関数式 [2]入力式 implicit_plot(x^2+y^2=1,[x,-2,2],[y,-2,2]); [3]描写結果 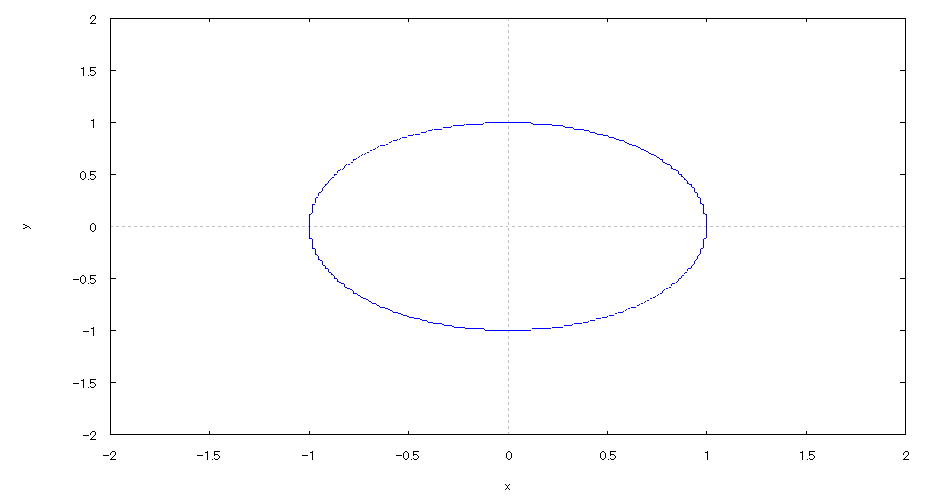 <グラフの描写方法> まず、load(implicit_plot) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 18】 2次元陰関数のグラフを描く。[四つ葉のクローバ] |
[1]関数式 [2]入力式 implicit_plot((x^2+y^2)^4-(x^2-y^2)^2=0,[x,-2,2],[y,-2,2]); [3]描写結果 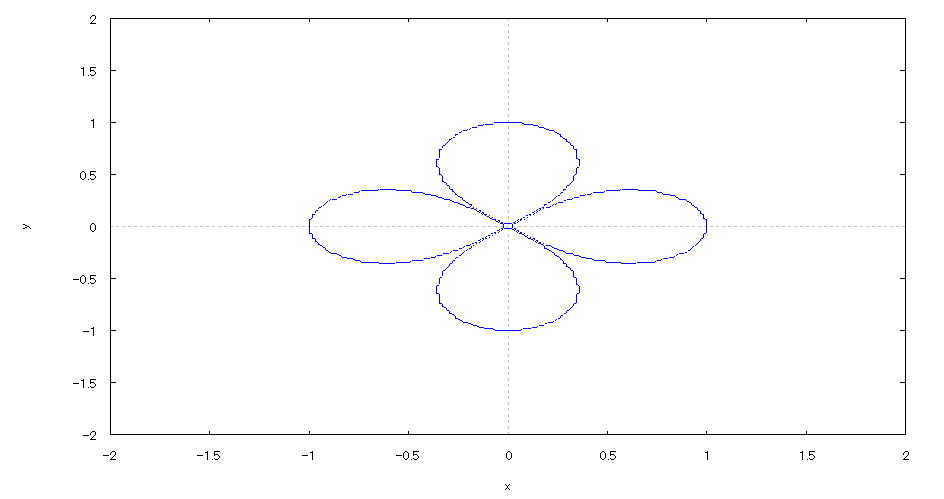 <グラフの描写方法> まず、load(implicit_plot) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 19】 2次元陰関数のグラフを描く。[円と四つ葉のクローバ] |
[1]関数式 [2]入力式 plot2d([x^2+y^2=1,(x^2+y^2)^4-(x^2-y^2)^2=0],[x,-2,2],[y,-2,2]); [3]描写結果 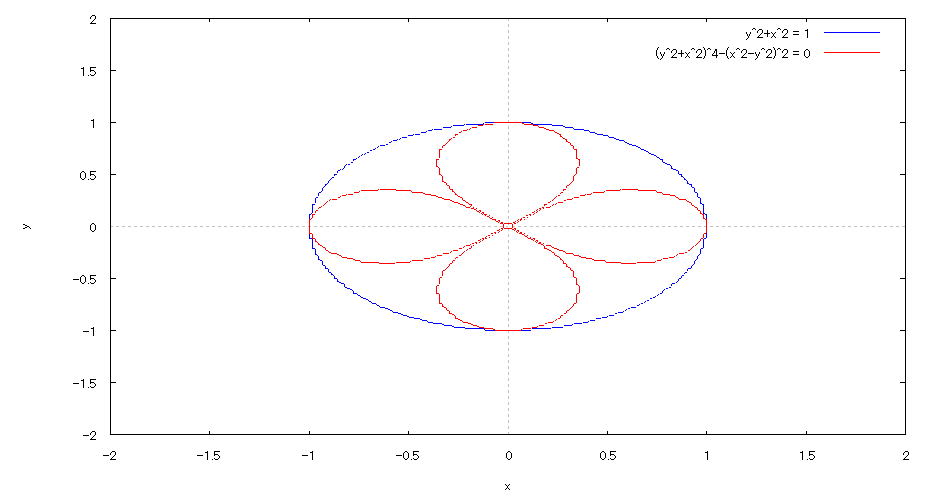 <グラフの描写方法> まず、load(implicit_plot) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 20】 2次元媒介変数のグラフを描く。[∞の形] |
[1]関数式 x=cost y=sin2t (0≦t≦2π) 100分割 [2]入力式 plot2d([parametric,cos(t),sin(2*t)],[t,0,2*%pi],[nticks,100]); [3]描写結果 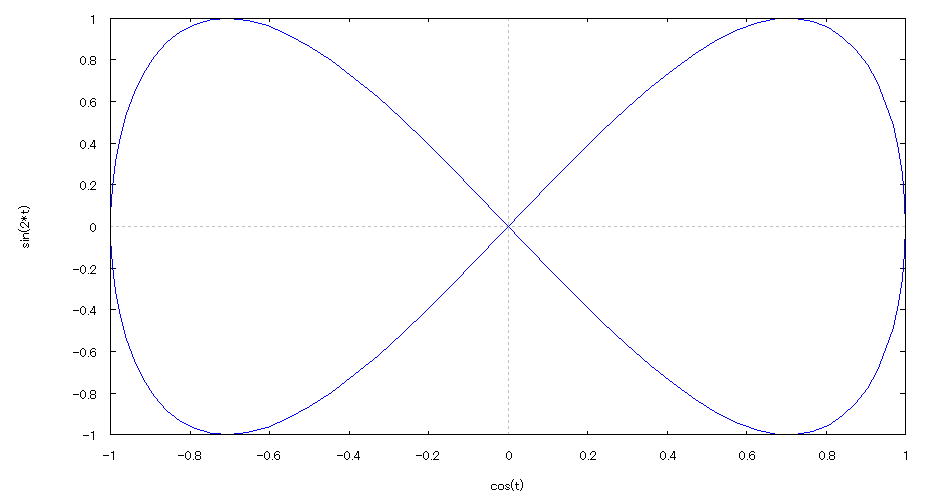 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 21】 2次元媒介変数のグラフを描く。[菊の花ビラの形] |
[1]関数式 x=4sin4tcost y=4sin4tsint (0≦t≦2π) 400分割 [2]入力式 plot2d([parametric,4*sin(4*t)*cos(t),4*sin(4*t)*sin(t)],[t,0,2*%pi],[nticks,400]); [3]描写結果 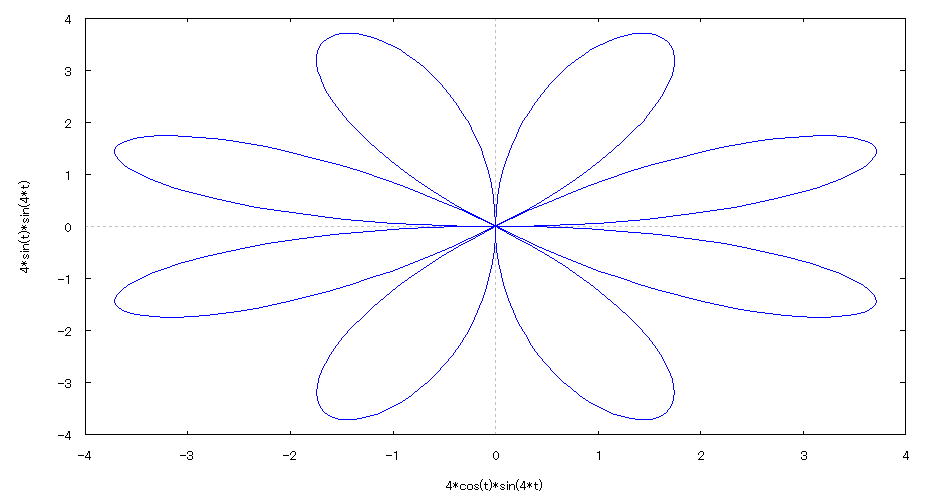 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 22】 2次元媒介変数のグラフを描く。[渦巻きの形] |
[1]関数式 x=tcost y=tsint [2]入力式 plot2d([parametric,t*cos(t),t*sin(t)],[t,0,35*%pi/2],[nticks,500]); [3]描写結果 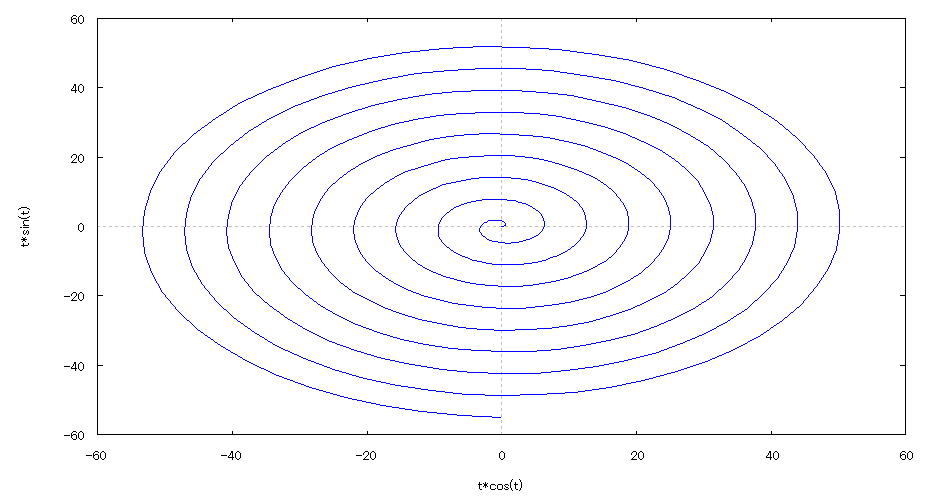 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 23】 2次元媒介変数のグラフを描く。[心臓の形] |
[1]関数式 x=(1+cost)cost y=(1+cost)sint (0≦t≦2π) 100分割 [2]入力式 plot2d([parametric,(1+cos(t))*cos(t),(1+cos(t))*sin(t)],[t,0,2*%pi],[nticks,100]); [3]描写結果 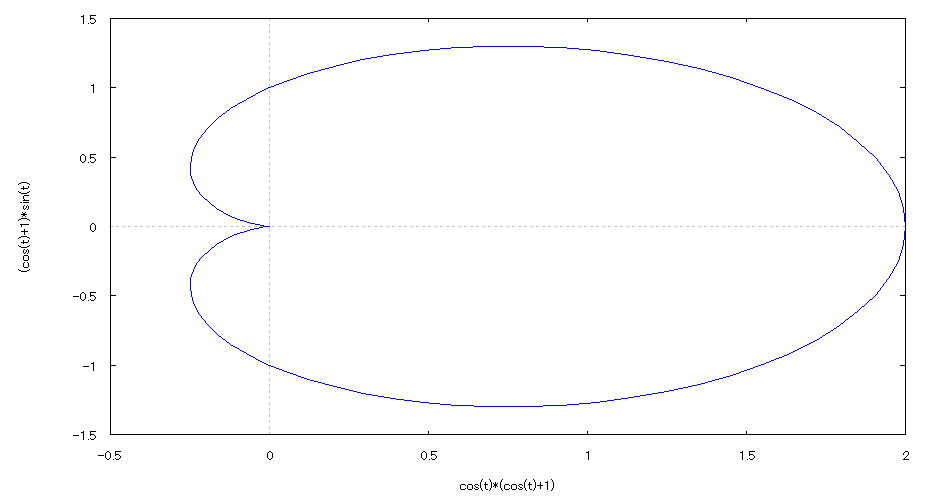 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 24】 3次元陰関数のグラフをワイヤーフレームで描く。[楕円面] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/1^2+y^2/2^2+z^2/3^2=1,x,-1,1,y,-2,2,z,-3,3)); [3]描写結果 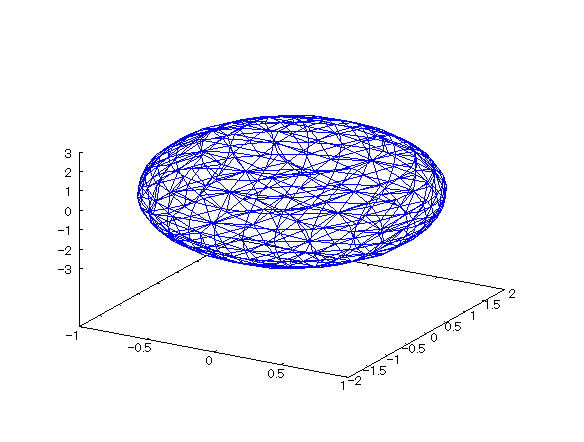 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 25】 3次元陰関数のグラフをワイヤーフレームで描く。[一葉双曲面] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/1^2+y^2/2^2-z^2/3^2=1,x,-7,7,y,-7,7,z,-7,7)); [3]描写結果 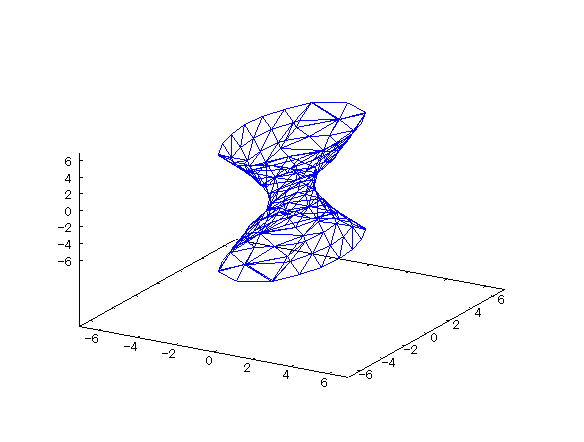 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 26】 3次元陰関数のグラフをワイヤーフレームで描く。[二葉双曲面] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/1^2-y^2/2^2-z^2/3^2=1,x,-2,2,y,-4,4,z,-8,8)); [3]描写結果 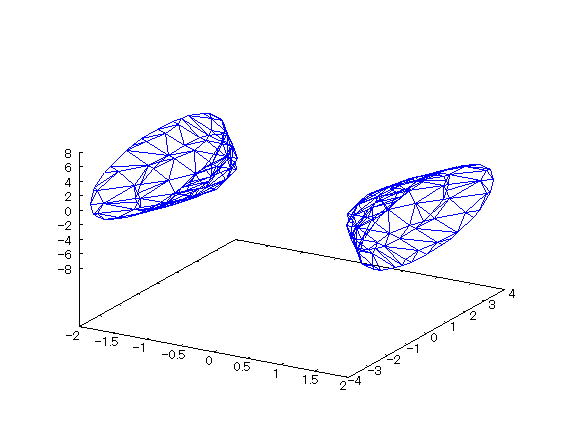 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 27】 3次元陰関数のグラフをワイヤーフレームで描く。[楕円放物面] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/1^2+y^2/2^2=1/20*z,x,-1,1,y,-2,2,z,0,20)); [3]描写結果 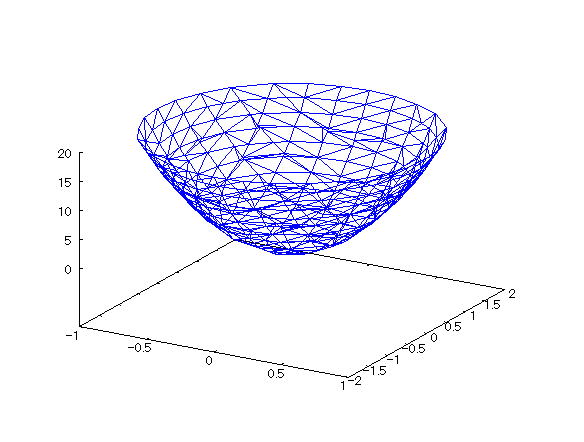 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 28】 3次元陰関数のグラフをワイヤーフレームで描く。[双曲放物面] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/1^2-y^2/2^2=1/2*z,x,-2,2,y,-3,3,z,-4,4)); [3]描写結果 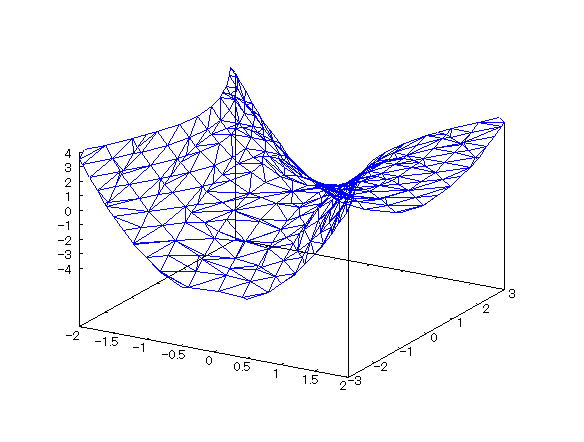 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 29】 3次元陰関数のグラフをワイヤーフレームで描く。[楕円柱] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/1^2+y^2/2^2=1,x,-2,2,y,-2,2,z,-10,10)); [3]描写結果 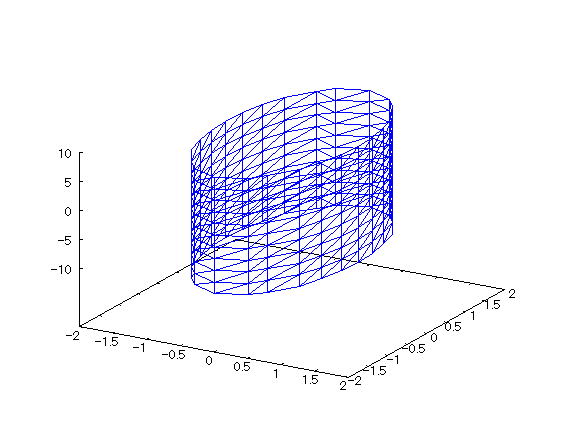 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 30】 3次元陰関数のグラフをワイヤーフレームで描く。[双曲柱] |
[1]関数式 [2]入力式 draw3d(implicit(x^2/2^2-y^2/3^2=1,x,-10,10,y,-10,10,z,-20,20)); [3]描写結果 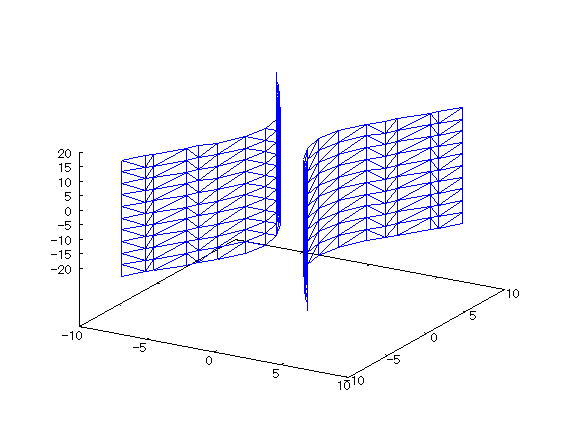 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 31】 3次元陰関数のグラフをワイヤーフレームで描く。[放物柱] |
[1]関数式 [2]入力式 draw3d(implicit(x^2=y,x,-5,5,y,0,25,z,-20,20)); [3]描写結果 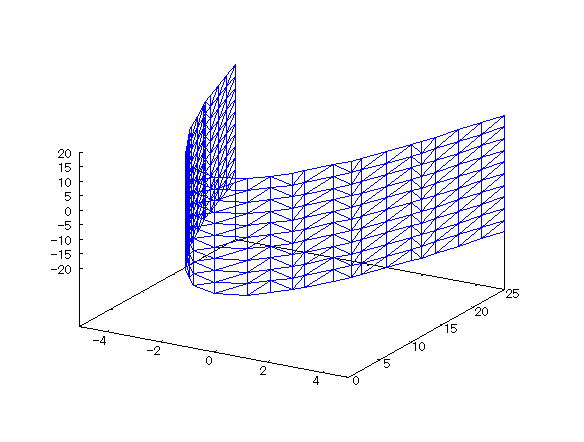 <グラフの描写方法> まず、load(draw) と入力し、Shiftキー と Enterキー を同時に押して、パッケージを読み込む。 次に、上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 32】 2次元陽関数のグラフを描く。[yの値の範囲を指定して見やすくする] |
[1]関数式 [2]入力式 plot2d((x^3+2*x^2-4*x-3)/(x+1),[x,-3,3],[y,-10,10]); [3]描写結果 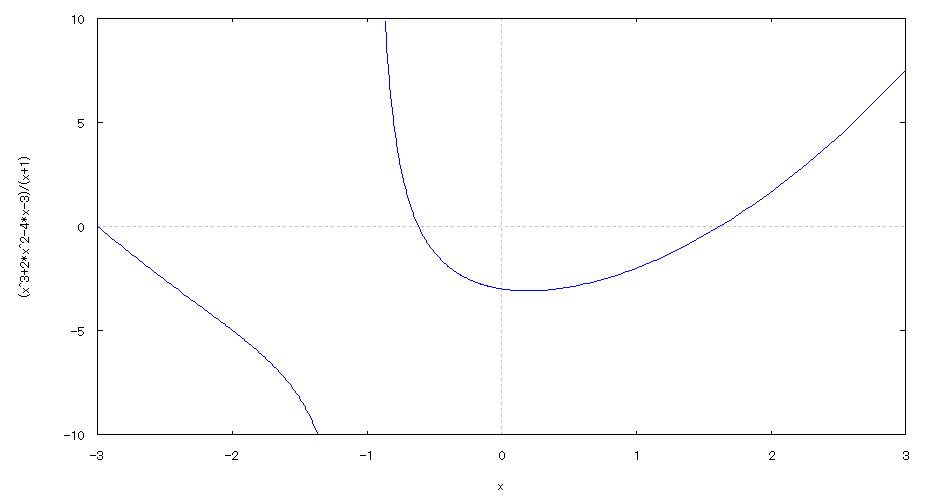 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 33】 2次元陽関数のグラフを描く。[複数のグラフを同時に表示する] |
[1]関数式 [2]入力式 plot2d([exp(-2*x),exp(x),1],[x,-2,2],[y,0,10]); [3]描写結果 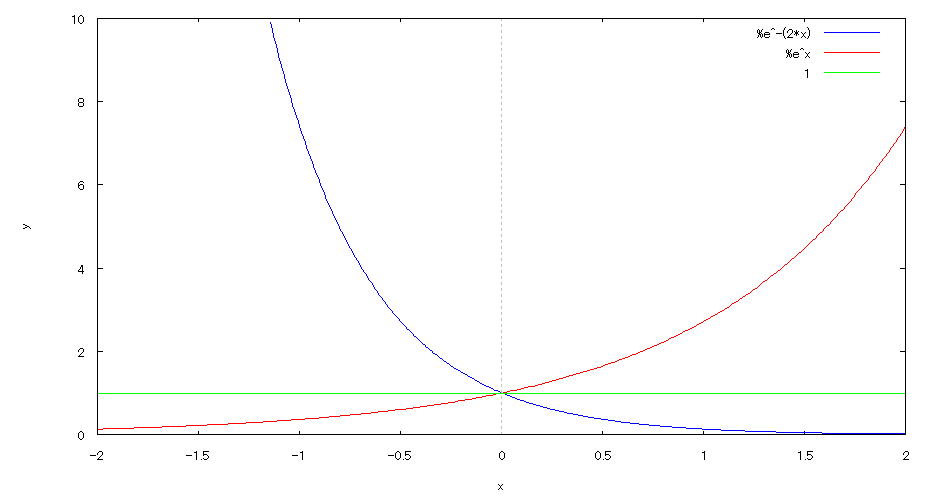 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 34】 2次元陽関数のグラフを描く。[方程式の実数解の個数を調べる] |
[1]方程式 [2]入力式 plot2d([x/8,cos(x)],[x,-15,15],[y,-2,2]); [3]描写結果 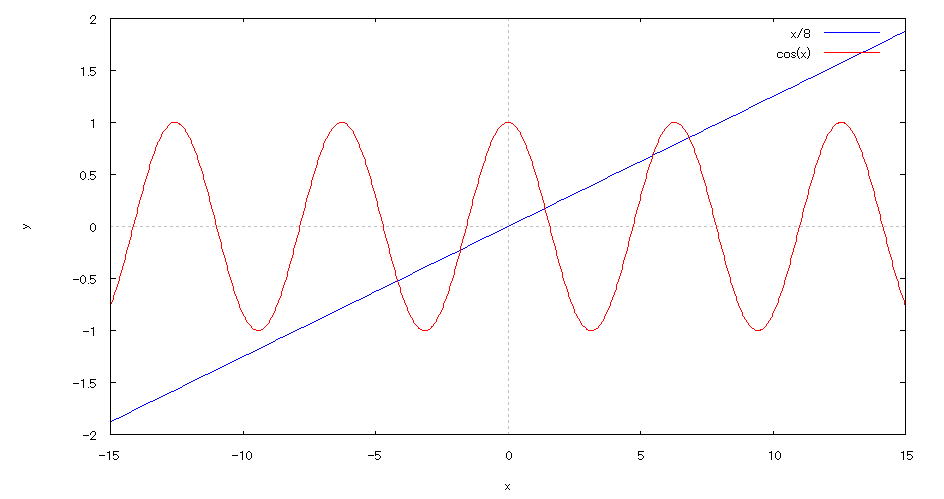 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 交点の個数が5個なので、方程式は5個の実数解をもつことが分かる。 |
| 【例 35】 2次元媒介変数のグラフを描く。[分割数を指定する] |
[1]関数式 [2]入力式 plot2d([parametric,3*cos(t)+cos(13*t),3*sin(t)+sin(13*t)],[t,0,2*%pi],[nticks,300]); [3]描写結果 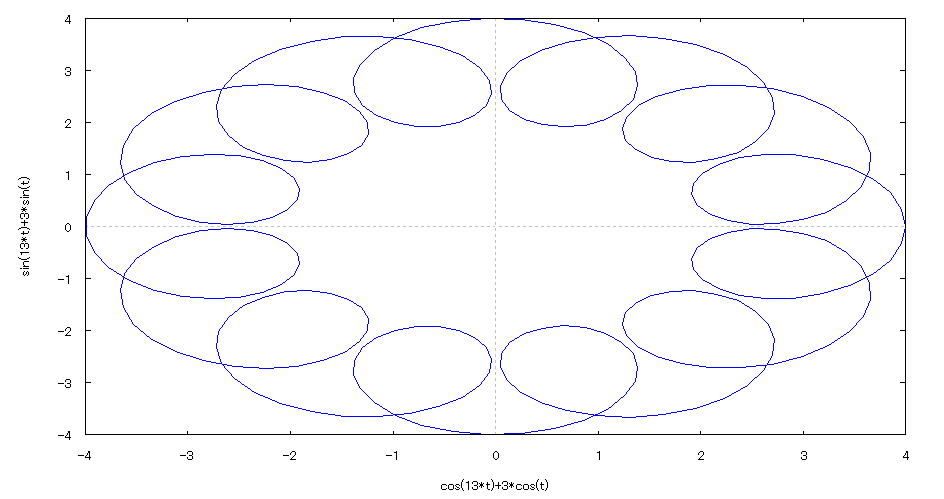 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 36】 2次元媒介変数のグラフを描く。[リサージュ曲線] |
[1]関数式 [2]入力式 plot2d([parametric,cos(7*t),sin(4*t)],[t,0,2*%pi],[nticks,300]); [3]描写結果 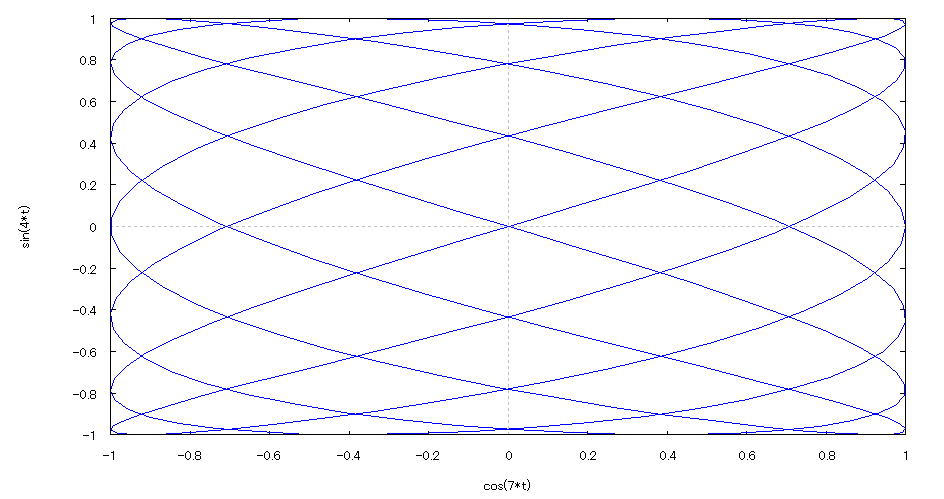 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 37】 2次元媒介変数のグラフを描く。[ベルヌーイのレムニスケート曲線] |
[1]関数式 [2]入力式 plot2d([parametric,cos(t)/(1+sin(t)^2),sin(t)*cos(t)/(1+sin(t)^2)],[t,0,2*%pi],[nticks,300]); [3]描写結果 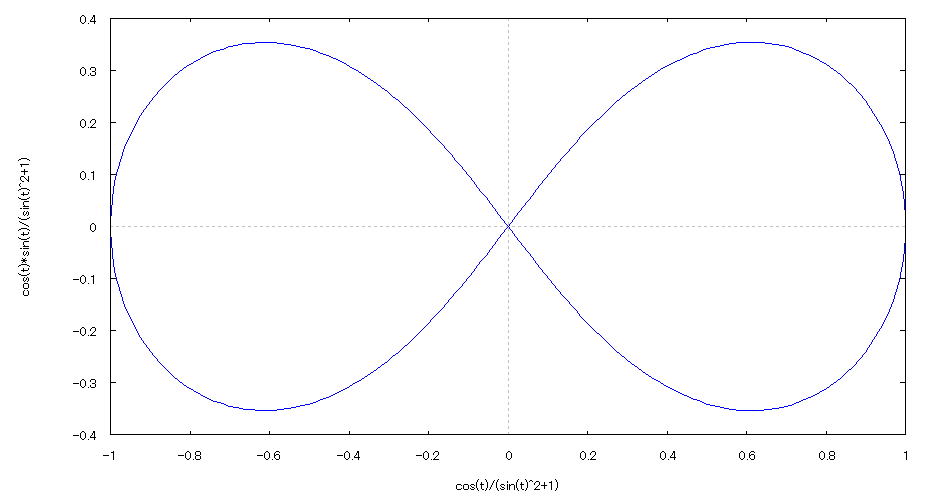 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 38】 3次元陽関数のグラフを描く。[分割数を指定しない] |
[1]関数式 [2]入力式 plot3d(exp(-sqrt(x^2+y^2)/2)*cos(%pi*sqrt(x^2+y^2)),[x,-4,4],[y,-4,4]); [3]描写結果 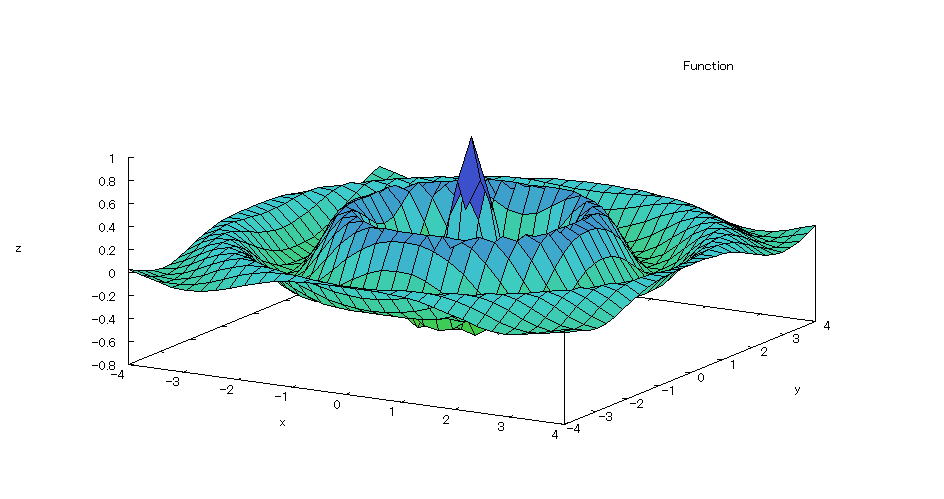 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 39】 3次元陽関数のグラフを描く。[シャークの極小曲面] |
[1]関数式 [2]入力式 plot3d(log(cos(x)/cos(y)),[x,-%pi/2,%pi/2],[y,-%pi/2,%pi/2]); [3]描写結果  <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 40】 3次元陽関数のグラフを描く。[関数を定義して描く] |
[1]関数式 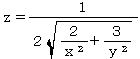 (0<x≦2,0<y≦2) (0<x≦2,0<y≦2)[2]入力式 u(a,x,y,p,q,r):=a*(p*x^(-r)+q*y^(-r))^(-1/r); plot3d(u(2,x,y,2,3,2),[x,0.01,2],[y,0.01,2]); [3]描写結果 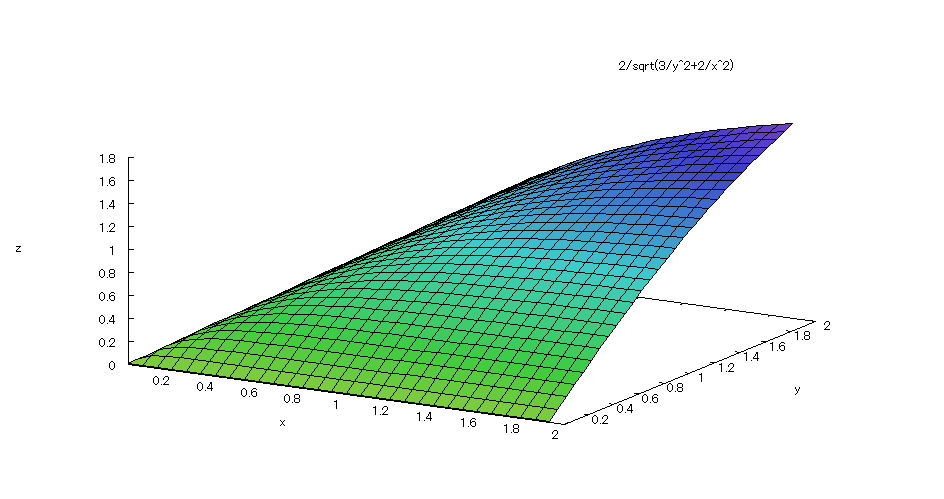 <グラフの描写方法> まず、上記の入力式の1行目を全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 次に、2行目を全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 41】 3次元媒介変数のグラフを描く。[トーラス] |
[1]関数式 0≦s≦2π、0≦t≦2π [2]入力式 plot3d([cos(s)*(3+cos(t)),sin(s)*(3+cos(t)),sin(t)],[s,0,2*%pi],[t,0,2*%pi]); [3]描写結果 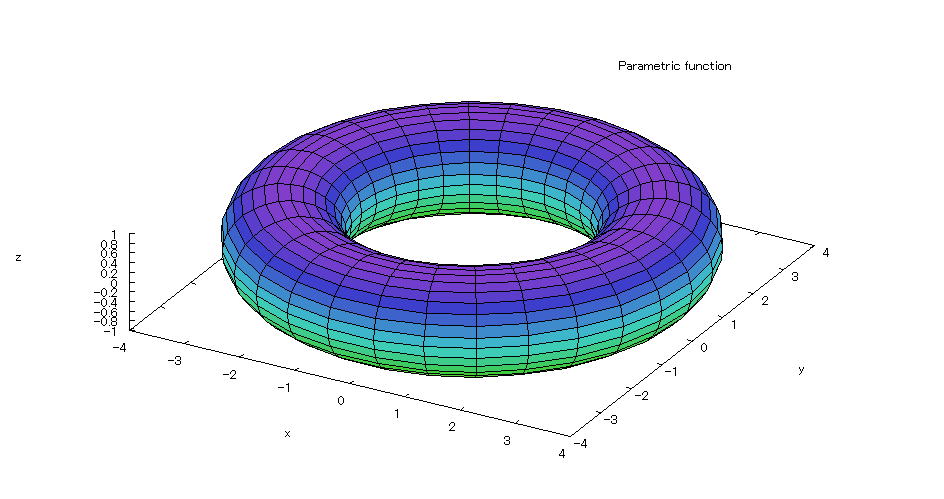 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 42】 3次元媒介変数のグラフを描く。[アステロイド的球面] |
[1]関数式 0≦s≦2π、0≦t≦2π [2]入力式 plot3d([cos(s)^3*cos(t)^3,sin(s)^3*cos(t)^3,sin(t)^3],[s,0,2*%pi],[t,0,2*%pi]); [3]描写結果 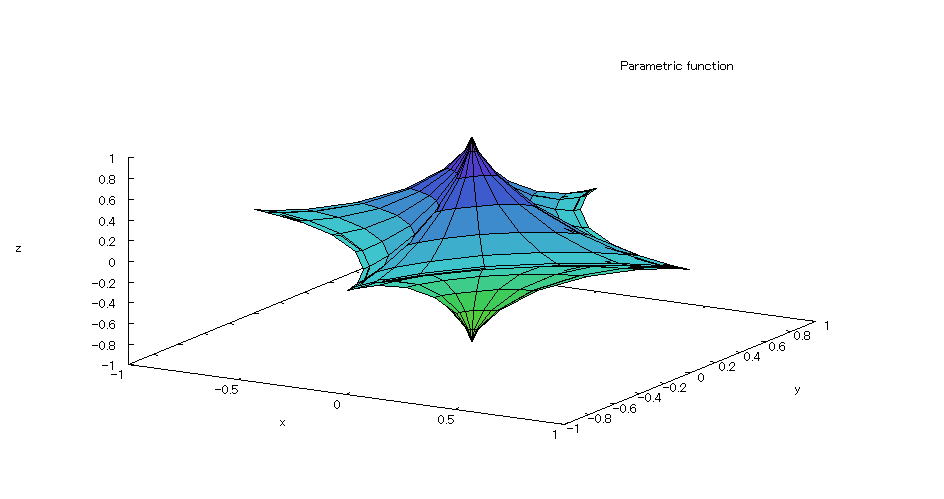 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 43】 3次元媒介変数のグラフを描く。[ヘンネベルグの極小曲面] |
[1]関数式 0.3≦s≦0.9 、 0≦t≦2π [2]入力式 plot3d([2*sinh(s)*cos(t)-(2/3)*sinh(3*s)*cos(3*t),2*sinh(s)*sin(t)-(2/3)*sinh(3*s) *sin(3*t),2*cosh(2*s)*cos(2*t)],[s,0.3,0.9],[t,0,2*%pi],[grid,4,72]); [3]描写結果 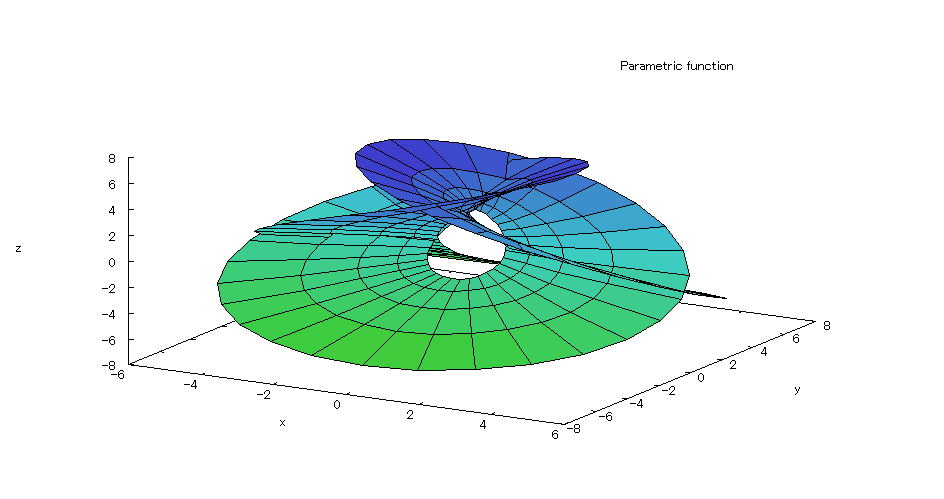 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 44】 2次元陽関数のグラフを描く。[yの値の範囲を指定して見やすくする] |
[1]関数式 [2]入力式 plot2d(1/(x-1)+1,[x,-5,5],[y,-5,5]); [3]描写結果 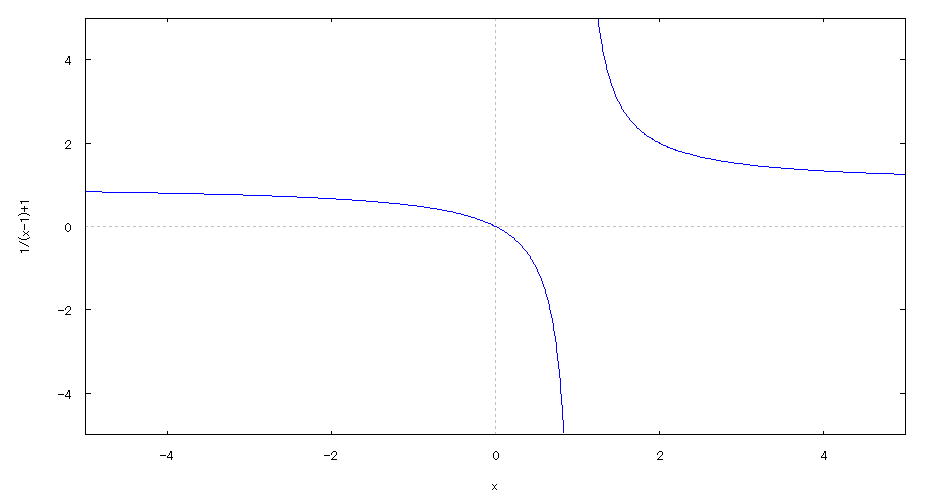 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 45】 2次元陽関数のグラフを描く。[テーラー展開した近似式のグラフと比較する] |
[1]関数式 [2]入力式 plot2d([cos(x),1-x^2/2+x^4/24-x^6/720,1-x^2/2+x^4/24-x^6/720+x^8/40320, 1-x^2/2+x^4/24-x^6/720+x^8/40320-x^10/3628800],[x,-2*%pi,2*%pi],[y,-5,5]); [3]描写結果 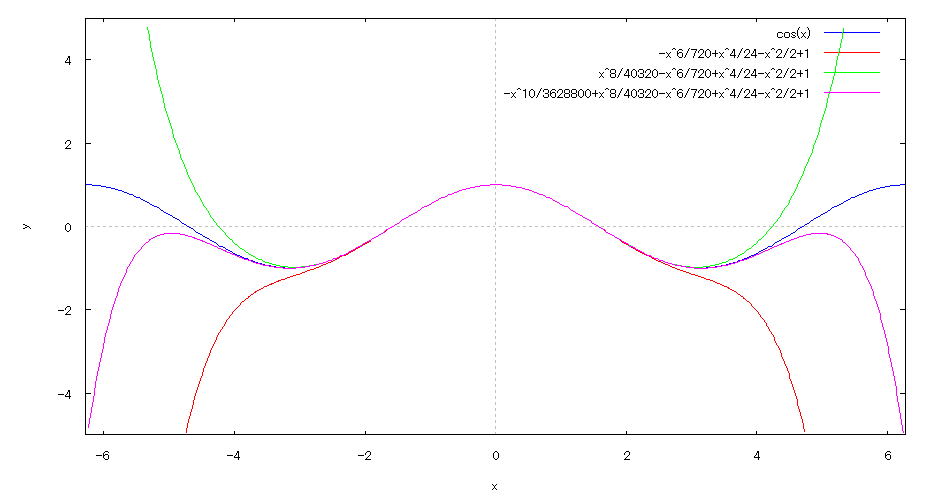 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 46】 2次元陽関数のグラフを描く。[方程式の実数解の個数を調べる] |
[1]方程式 [2]入力式 plot2d([exp(x),3-x^2],[x,-2,2],[y,-1,4]); [3]描写結果 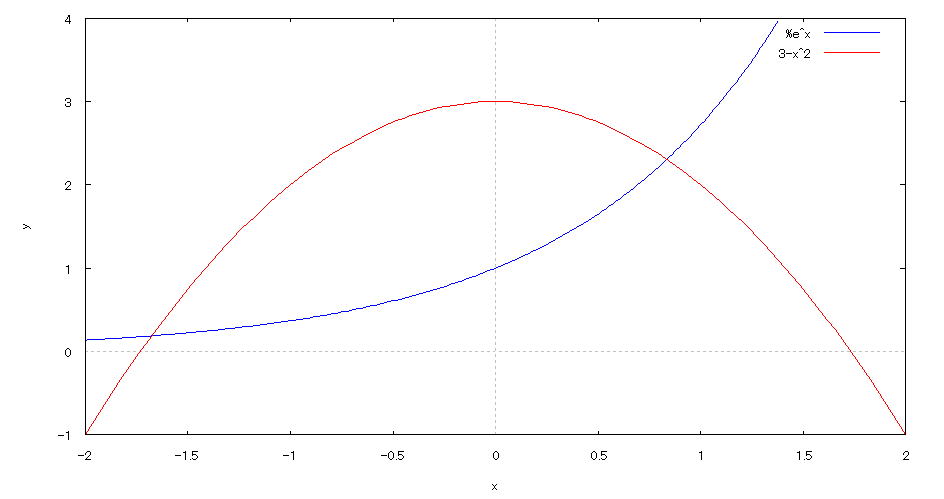 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 交点の個数が2個なので、方程式は2個の実数解をもつことが分かる。 |
| 【例 47】 2次元媒介変数のグラフを描く。[円:分割数を指定しない] |
[1]関数式 [2]入力式 plot2d([parametric,cos(t),sin(t)],[t,0,2*%pi]); [3]描写結果 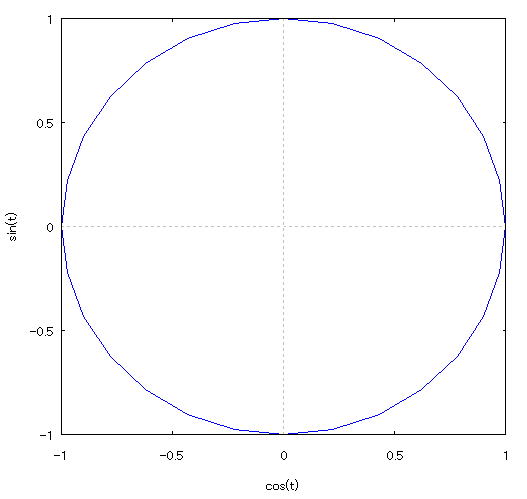 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 48】 2次元媒介変数のグラフを描く。[円:分割数15を指定する] |
[1]関数式 [2]入力式 plot2d([parametric,cos(t),sin(t)],[t,0,2*%pi],[nticks,15]); [3]描写結果 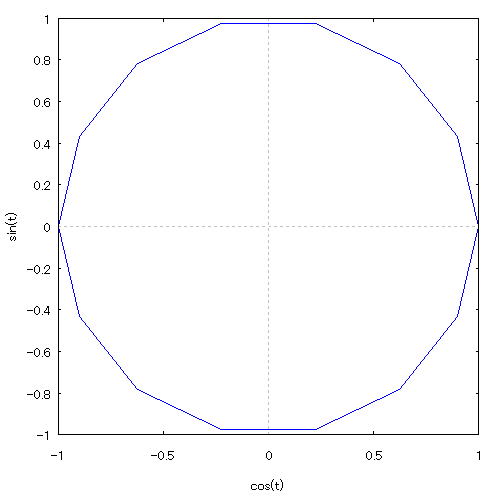 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 49】 2次元媒介変数のグラフを描く。[円:分割数100を指定する] |
[1]関数式 [2]入力式 plot2d([parametric,cos(t),sin(t)],[t,0,2*%pi],[nticks,100]); [3]描写結果 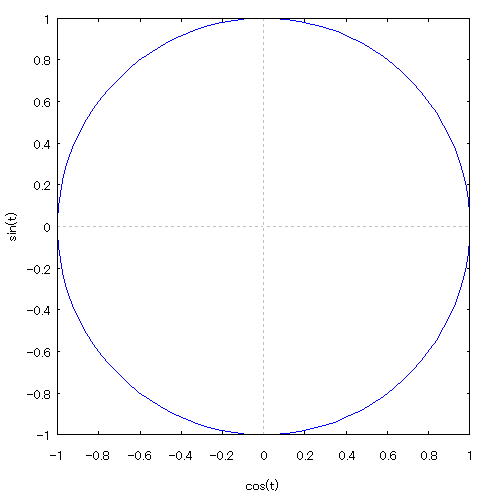 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 50】 3次元陽関数のグラフを描く。[分割数を指定しない] |
[1]関数式 [2]入力式 plot3d(x^3-3*x*y^2,[x,-1,1],[y,-1,1]); [3]描写結果 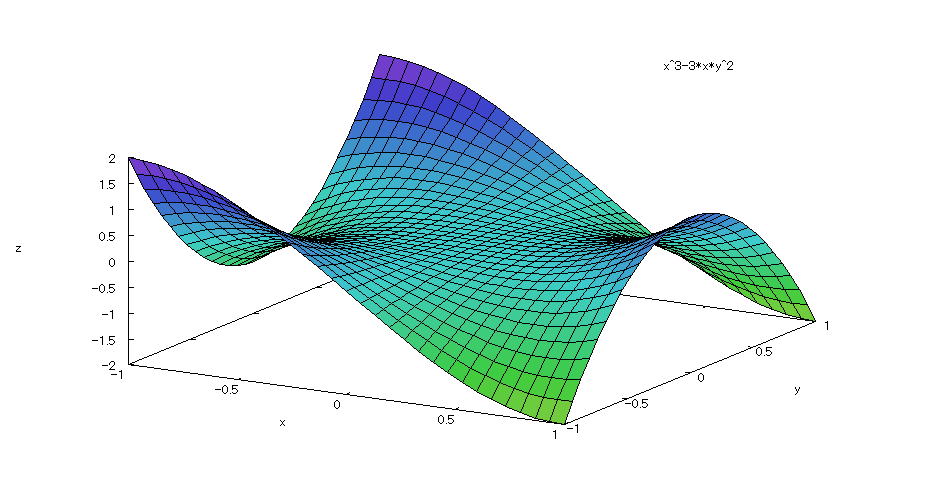 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 51】 3次元陽関数のグラフを描く。[分割数を指定しない] |
[1]関数式 [2]入力式 plot3d((x^2*y)/(x^4+y^2),[x,-1,1],[y,-1,1]); [3]描写結果 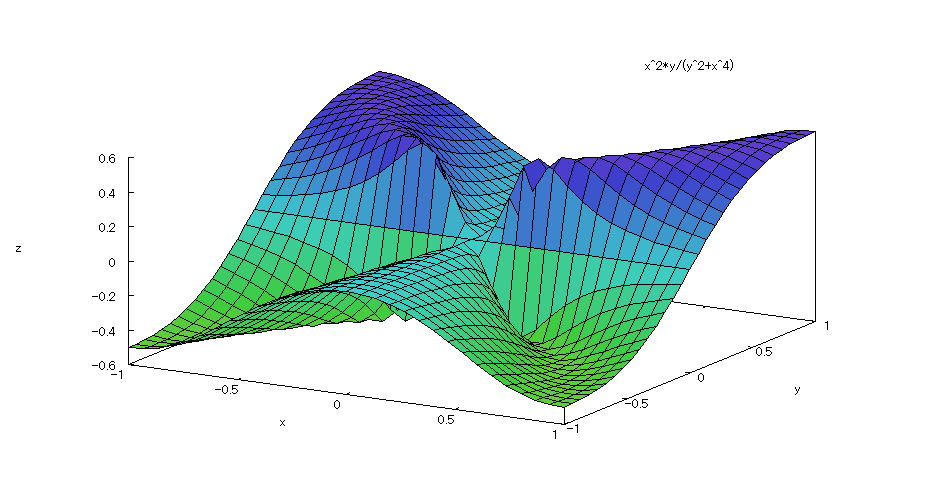 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 52】 3次元陽関数のグラフを描く。[分割数を指定する] |
[1]関数式 [2]入力式 plot3d((x^2*y)/(x^4+y^2),[x,-1,1],[y,-1,1],[grid,100,100]); [3]描写結果 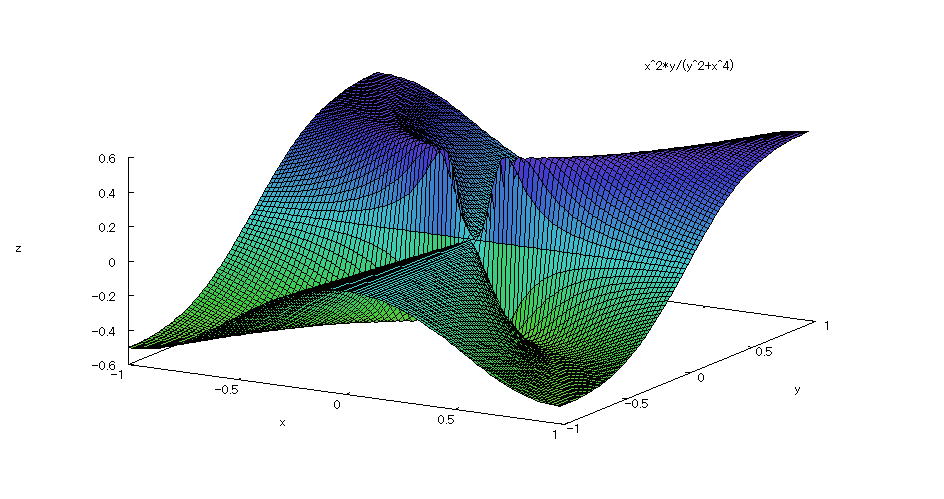 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 53】 3次元媒介変数のグラフを描く。[球面:分割数を指定する] |
[1]関数式 0≦s≦2π、0≦t≦2π [2]入力式 plot3d([cos(s)*cos(t),cos(s)*sin(t),sin(s)],[s,0,2*%pi],[t,0,2*%pi],[grid,50,50]); [3]描写結果 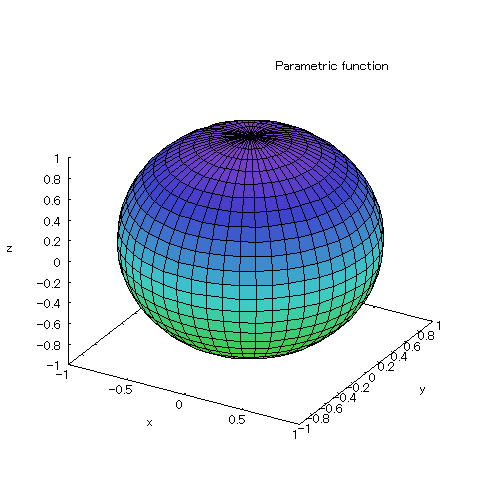 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 54】 3次元媒介変数のグラフを描く。[驚きの図形と方程式] |
[1]関数式 0≦u≦2π、0≦v≦2π [2]入力式 plot3d([3*cos(u)+5*cos(3*u)+(3*(cos(u)+5*cos(3*u))*cos(v))/(2*sqrt(234+90*cos(2*u))) -(3*cos(6*u)*(sin(u)+5*sin(3*u))*sin(v))/(2*sqrt(13+5*cos(2*u))*sqrt(22+5*cos(2*u) +9*cos(12*u))),3*sin(u)+5*sin(3*u)+(3*cos(v)*(sin(u)+5*sin(3*u)))/(2*sqrt(234+90*cos (2*u)))+(3*(5*cos(3*u)+cos(5*u)+cos(7*u)+5*cos(9*u))*sin(v))/(4*sqrt(13+5*cos(2*u)) *sqrt(22+5*cos(2*u)+9*cos(12*u))),3*sin(6*u)-(sqrt(13+5*cos(2*u))*sin(v))/(2*sqrt (22+5*cos(2*u)+9*cos(12*u)))],[u,0,2*%pi],[v,0,2*%pi],[grid,80,8]); [3]描写結果 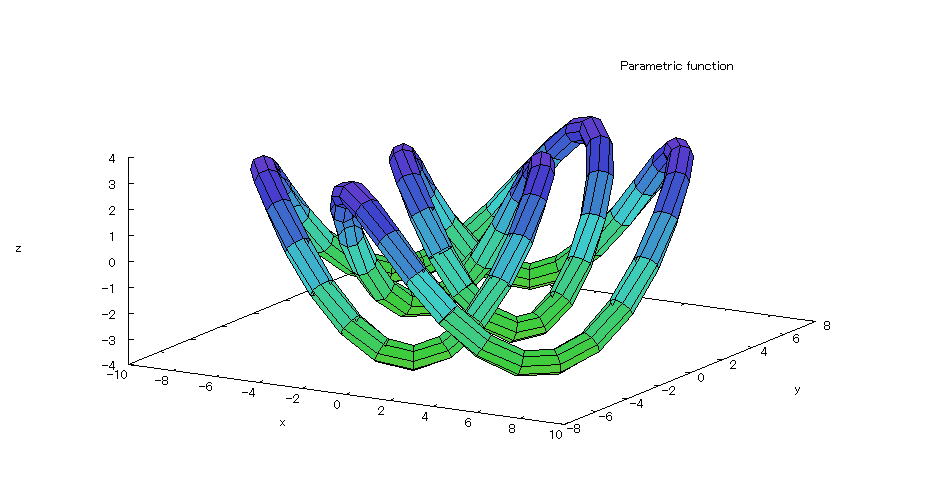 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 55】 3次元媒介変数のグラフを描く。[回転体1] |
[1]回転体 [2]入力式 plot3d([t,t^2*cos(s),t^2*sin(s)],[t,-3,3],[s,0,2*%pi]); [3]描写結果 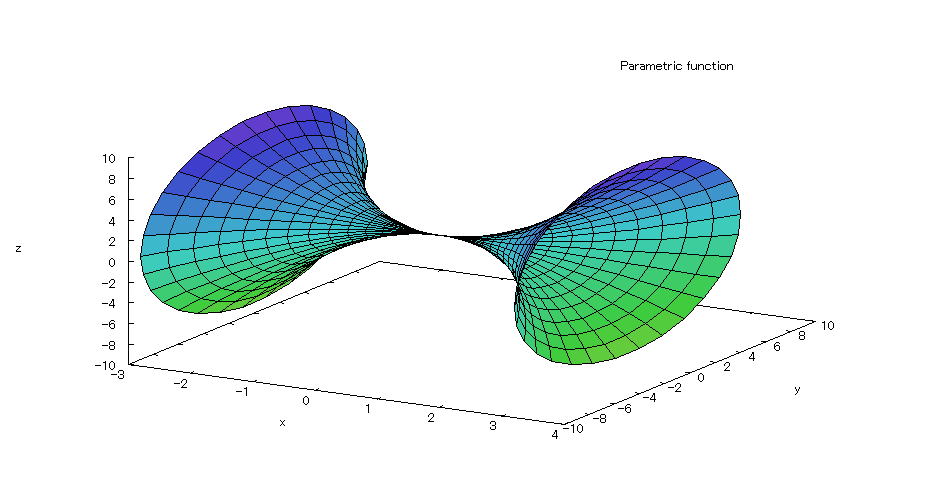 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 56】 3次元媒介変数のグラフを描く。[回転体2] |
[1]回転体 [2]入力式 plot3d([sqrt(t)*cos(s),t,sqrt(t)*sin(s)],[t,0,9],[s,0,2*%pi]); [3]描写結果 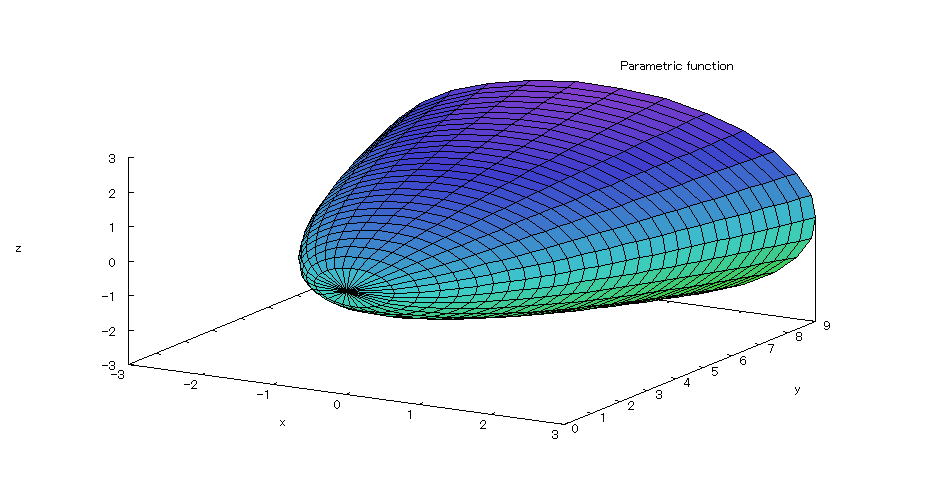 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 57】 3次元媒介変数のグラフを描く。[回転体3] |
[1]回転体 [2]入力式 plot3d([t,(t^2-2)*cos(s),(t^2-2)*sin(s)],[t,-3,3],[s,0,2*%pi]); [3]描写結果 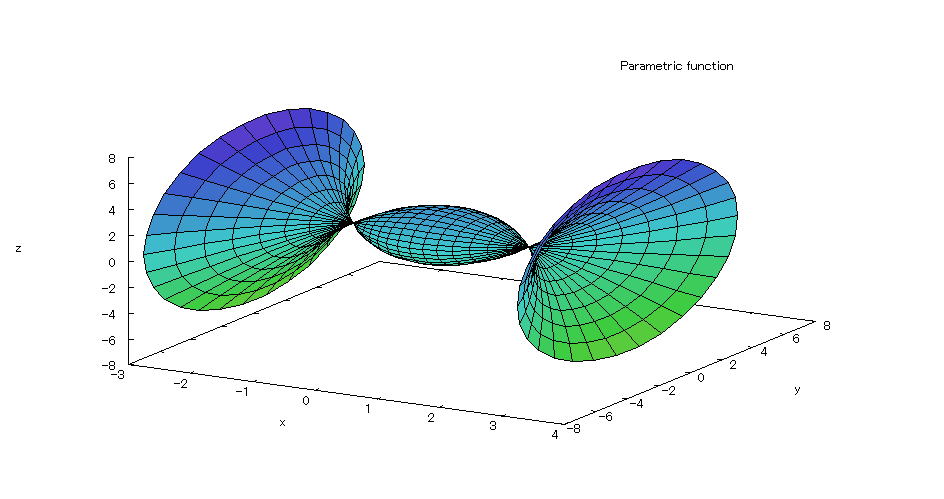 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 58】 3次元媒介変数のグラフを描く。[回転体4] |
[1]回転体 [2]入力式 plot3d([t,(t^2+2)*cos(s),(t^2+2)*sin(s)],[t,-2,2],[s,0,2*%pi]); [3]描写結果 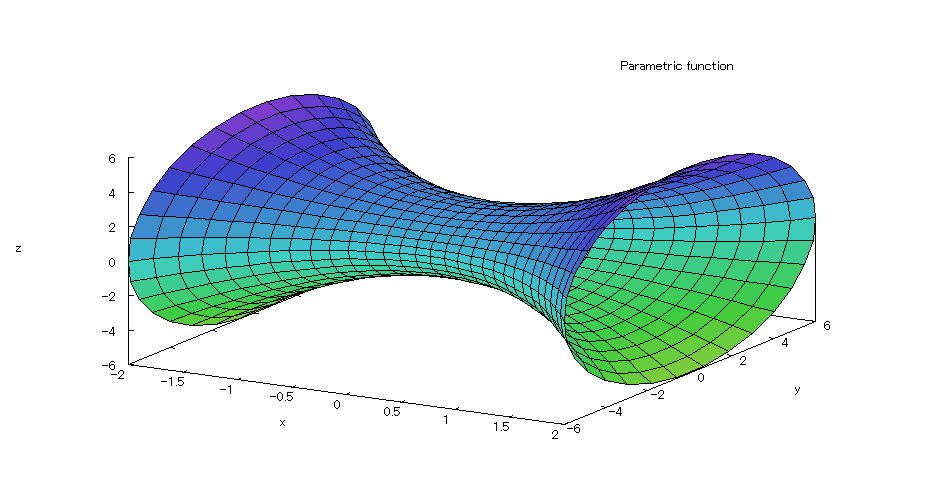 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 59】 3次元媒介変数のグラフを描く。[回転体5] |
[1]回転体 [2]入力式 plot3d([t,sqrt(4-t^2)*cos(s),sqrt(4-t^2)*sin(s)],[t,-2,2],[s,0,2*%pi]); [3]描写結果 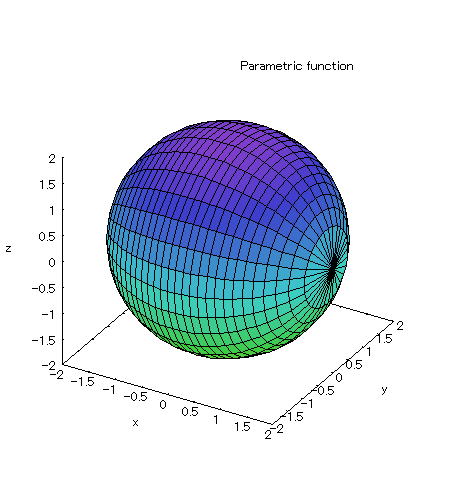 <グラフの描写方法> 上記の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 60】 テーラー展開による式の近似 [y=sinx] |
[1]sinx をテーラー展開する入力式 taylor(sin(x),x,0,12); [2]展開結果 [3]y=sinx のグラフとその近似式のグラフを描写する入力式 plot2d([sin(x),x-x^3/6+x^5/120-x^7/5040+x^9/362880-x^11/39916800],[x,-10,10],[y,-1.2,1.2]); [4]描写結果 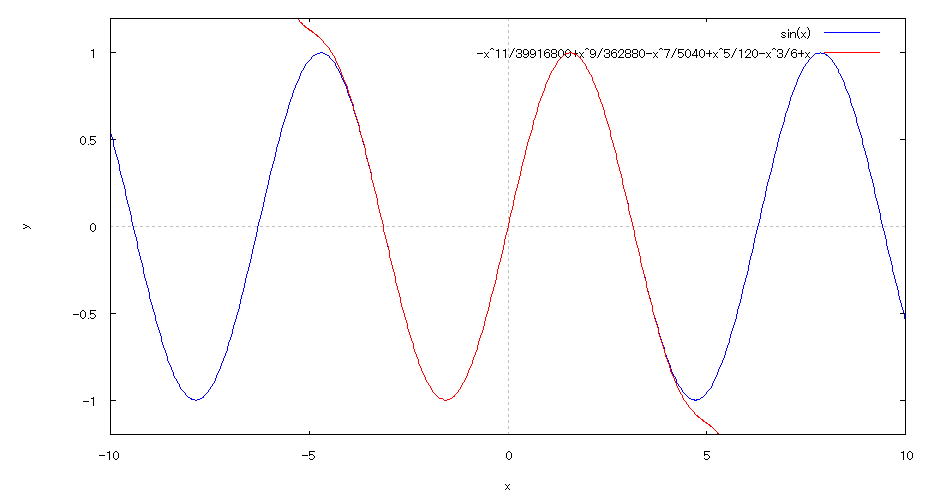 <グラフの描写方法> 上記[3]の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 61】 テーラー展開による式の近似 [y=cosx] |
[1]cosx をテーラー展開する入力式 taylor(cos(x),x,0,12); [2]展開結果 [3]y=cosx のグラフとその近似式のグラフを描写する入力式 plot2d([cos(x),1-x^2/2+x^4/24-x^6/720+x^8/40320-x^10/3628800+x^12/479001600] ,[x,-10,10],[y,-1.2,1.2]); [4]描写結果 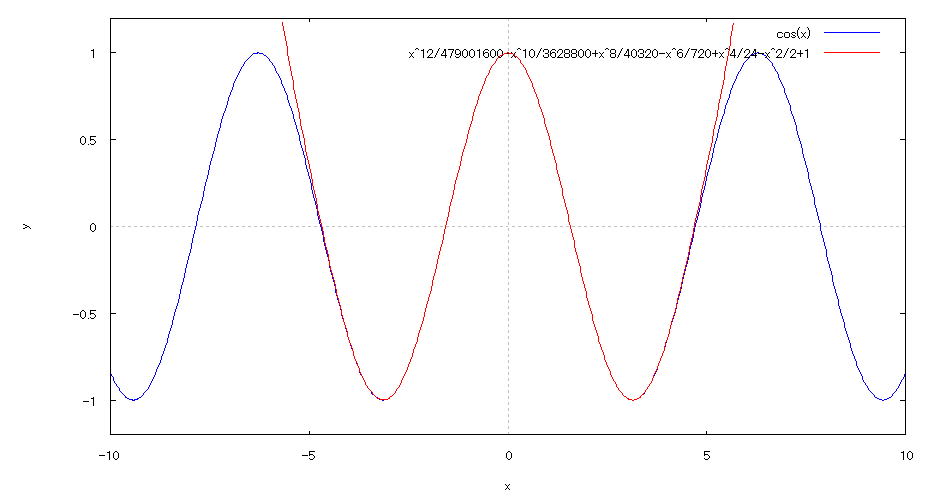 <グラフの描写方法> 上記[3]の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 62】 テーラー展開による式の近似 |
[1] taylor(exp(x),x,0,6); [2]展開結果 1+x+x^2/2+x^3/6+x^4/24+x^5/120+... [3] plot2d([exp(x),1+x+x^2/2+x^3/6+x^4/24+x^5/120],[x,-3,3],[y,0,5]); [4]描写結果 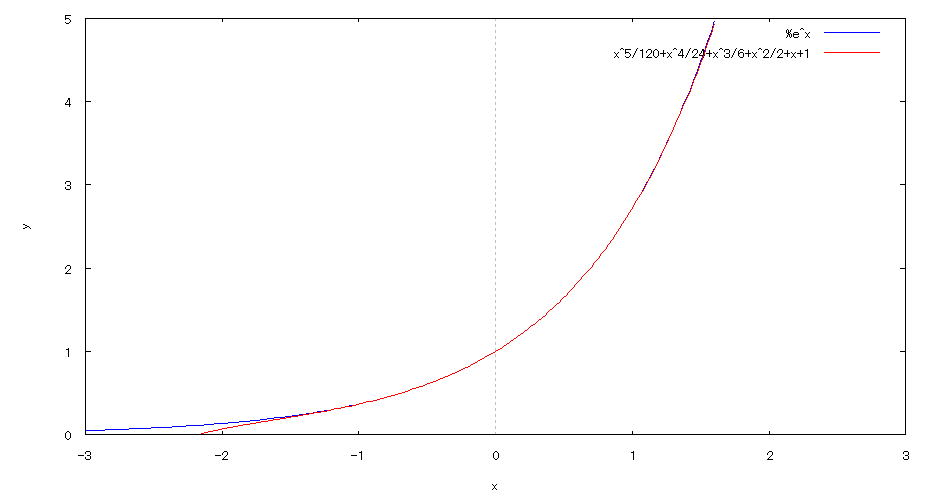 <グラフの描写方法> 上記[3]の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【例 63】 オイラーの公式 |
[1]sinx をテーラー展開する入力式 taylor(sin(x),x,0,12); [2]sinx のテーラー展開結果 [3]cosx をテーラー展開する入力式 taylor(cos(x),x,0,12); [4]cosx のテーラー展開結果 [5] taylor(exp(%i*x),x,0,12); [6] ---③ 以上 ①、②、③より、 = cosx + isinx よって、 <展開式の表示方法> 上記[1][3][5]の入力式のように全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【問題 1】 2^30 は何桁の整数になるか。 ただし、log(10,2)=0.3010 とする。 |
| この問題は常用対数のところで必ず出てくる問題である。 以下の ①→②→③→④ の順序で指導すれば、桁数をより具体的にすることができるはずである。 ①2^30、2^50、2^100、3^30、3^50、3^100 を『Maxima』に計算させたものを提示し、その桁数を数えさせる。 ②常用対数を用いた桁数の求め方を指導する。 ③2^30、2^50、2^100、3^30、3^50、3^100 を常用対数を用いて求めさせ、先ほど数えた桁数と一致していることを確かめさる。 ④大きな数の数え方に触れる。 (おく)(ちょう)(けい)(がい)(じょ)(じょう)(こう)(かん)(せい)(さい)(ごく)(ごうがしゃ)(あそうぎ)(なゆた)(ふかしぎ)(むりょうたいすう) 以下、『Maxima』に計算させた結果である。 2^30=1073741824 2^50=1125899906842624 2^100=1267650600228229401496703205376 3^30=205891132094649 3^50=717897987691852588770249 3^100=515377520732011331036461129765621272702107522001 <『Maxima』の使い方> 例えば、2^30 を計算させる場合 2^30 と全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【問題 2】 (a+b)^3 及び (a+b+c)^2 を展開しなさい。 |
| (a+b)^3 や (a+b+c)^2 を展開しても、あまり驚きを感じられるものでない。 「式の展開」の指導の導入で、(a+b)^50 の展開や(a+b+c)^20 の展開を『Maxima』に計算させて提示したら、生徒に驚きや感動を与えられる授業がでないだろうか。 以下、『Maxima』に展開させた結果である。 (a+b)^50 =b^50+50*a*b^49+1225*a^2*b^48+19600*a^3*b^47+230300*a^4*b^46+2118760*a^5*b^45 +15890700*a^6*b^44+99884400*a^7*b^43+536878650*a^8*b^42+2505433700*a^9*b^41 +10272278170*a^10*b^40+37353738800*a^11*b^39+121399651100*a^12*b^38 +354860518600*a^13*b^37+937845656300*a^14*b^36+2250829575120*a^15*b^35 +4923689695575*a^16*b^34+9847379391150*a^17*b^33+18053528883775*a^18*b^32 +30405943383200*a^19*b^31+47129212243960*a^20*b^30+67327446062800*a^21*b^29 +88749815264600*a^22*b^28+108043253365600*a^23*b^27+121548660036300*a^24*b^26 +126410606437752*a^25*b^25+121548660036300*a^26*b^24+108043253365600*a^27*b^23 +88749815264600*a^28*b^22+67327446062800*a^29*b^21+47129212243960*a^30*b^20 +30405943383200*a^31*b^19+18053528883775*a^32*b^18+9847379391150*a^33*b^17 +4923689695575*a^34*b^16+2250829575120*a^35*b^15+937845656300*a^36*b^14 +354860518600*a^37*b^13+121399651100*a^38*b^12+37353738800*a^39*b^11 +10272278170*a^40*b^10+2505433700*a^41*b^9+536878650*a^42*b^8+99884400*a^43*b^7 +15890700*a^44*b^6+2118760*a^45*b^5+230300*a^46*b^4+19600*a^47*b^3+1225*a^48*b^2 +50*a^49*b+a^50 (a+b+c)^20 =c^20+20*b*c^19+20*a*c^19+190*b^2*c^18+380*a*b*c^18+190*a^2*c^18+1140*b^3*c^17 +3420*a*b^2*c^17+3420*a^2*b*c^17+1140*a^3*c^17+4845*b^4*c^16+19380*a*b^3*c^16 +29070*a^2*b^2*c^16+19380*a^3*b*c^16+4845*a^4*c^16+15504*b^5*c^15+77520*a*b^4*c^15 +155040*a^2*b^3*c^15+155040*a^3*b^2*c^15+77520*a^4*b*c^15+15504*a^5*c^15 +38760*b^6*c^14+232560*a*b^5*c^14+581400*a^2*b^4*c^14+775200*a^3*b^3*c^14 +581400*a^4*b^2*c^14+232560*a^5*b*c^14+38760*a^6*c^14+77520*b^7*c^13 +542640*a*b^6*c^13+1627920*a^2*b^5*c^13+2713200*a^3*b^4*c^13+2713200*a^4*b^3*c^13 +1627920*a^5*b^2*c^13+542640*a^6*b*c^13+77520*a^7*c^13+125970*b^8*c^12 +1007760*a*b^7*c^12+3527160*a^2*b^6*c^12+7054320*a^3*b^5*c^12 +8817900*a^4*b^4*c^12+7054320*a^5*b^3*c^12+3527160*a^6*b^2*c^12 +1007760*a^7*b*c^12+125970*a^8*c^12+167960*b^9*c^11+1511640*a*b^8*c^11 +6046560*a^2*b^7*c^11+14108640*a^3*b^6*c^11+21162960*a^4*b^5*c^11 +21162960*a^5*b^4*c^11+14108640*a^6*b^3*c^11+6046560*a^7*b^2*c^11 +1511640*a^8*b*c^11+167960*a^9*c^11+184756*b^10*c^10+1847560*a*b^9*c^10 +8314020*a^2*b^8*c^10+22170720*a^3*b^7*c^10+38798760*a^4*b^6*c^10 +46558512*a^5*b^5*c^10+38798760*a^6*b^4*c^10+22170720*a^7*b^3*c^10 +8314020*a^8*b^2*c^10+1847560*a^9*b*c^10+184756*a^10*c^10+167960*b^11*c^9 +1847560*a*b^10*c^9+9237800*a^2*b^9*c^9+27713400*a^3*b^8*c^9 +55426800*a^4*b^7*c^9+77597520*a^5*b^6*c^9+77597520*a^6*b^5*c^9 +55426800*a^7*b^4*c^9+27713400*a^8*b^3*c^9+9237800*a^9*b^2*c^9 +1847560*a^10*b*c^9+167960*a^11*c^9+125970*b^12*c^8+1511640*a*b^11*c^8 +8314020*a^2*b^10*c^8+27713400*a^3*b^9*c^8+62355150*a^4*b^8*c^8 +99768240*a^5*b^7*c^8+116396280*a^6*b^6*c^8+99768240*a^7*b^5*c^8 +62355150*a^8*b^4*c^8+27713400*a^9*b^3*c^8+8314020*a^10*b^2*c^8 +1511640*a^11*b*c^8+125970*a^12*c^8+77520*b^13*c^7+1007760*a*b^12*c^7 +6046560*a^2*b^11*c^7+22170720*a^3*b^10*c^7+55426800*a^4*b^9*c^7 +99768240*a^5*b^8*c^7+133024320*a^6*b^7*c^7+133024320*a^7*b^6*c^7 +99768240*a^8*b^5*c^7+55426800*a^9*b^4*c^7+22170720*a^10*b^3*c^7 +6046560*a^11*b^2*c^7+1007760*a^12*b*c^7+77520*a^13*c^7+38760*b^14*c^6 +542640*a*b^13*c^6+3527160*a^2*b^12*c^6+14108640*a^3*b^11*c^6 +38798760*a^4*b^10*c^6+77597520*a^5*b^9*c^6+116396280*a^6*b^8*c^6 +133024320*a^7*b^7*c^6+116396280*a^8*b^6*c^6+77597520*a^9*b^5*c^6 +38798760*a^10*b^4*c^6+14108640*a^11*b^3*c^6+3527160*a^12*b^2*c^6 +542640*a^13*b*c^6+38760*a^14*c^6+15504*b^15*c^5+232560*a*b^14*c^5 +1627920*a^2*b^13*c^5+7054320*a^3*b^12*c^5+21162960*a^4*b^11*c^5 +46558512*a^5*b^10*c^5+77597520*a^6*b^9*c^5+99768240*a^7*b^8*c^5 +99768240*a^8*b^7*c^5+77597520*a^9*b^6*c^5+46558512*a^10*b^5*c^5 +21162960*a^11*b^4*c^5+7054320*a^12*b^3*c^5+1627920*a^13*b^2*c^5 +232560*a^14*b*c^5+15504*a^15*c^5+4845*b^16*c^4+77520*a*b^15*c^4 +581400*a^2*b^14*c^4+2713200*a^3*b^13*c^4+8817900*a^4*b^12*c^4 +21162960*a^5*b^11*c^4+38798760*a^6*b^10*c^4+55426800*a^7*b^9*c^4 +62355150*a^8*b^8*c^4+55426800*a^9*b^7*c^4+38798760*a^10*b^6*c^4 +21162960*a^11*b^5*c^4+8817900*a^12*b^4*c^4+2713200*a^13*b^3*c^4 +581400*a^14*b^2*c^4+77520*a^15*b*c^4+4845*a^16*c^4+1140*b^17*c^3 +19380*a*b^16*c^3+155040*a^2*b^15*c^3+775200*a^3*b^14*c^3 +2713200*a^4*b^13*c^3+7054320*a^5*b^12*c^3+14108640*a^6*b^11*c^3 +22170720*a^7*b^10*c^3+27713400*a^8*b^9*c^3+27713400*a^9*b^8*c^3 +22170720*a^10*b^7*c^3+14108640*a^11*b^6*c^3+7054320*a^12*b^5*c^3 +2713200*a^13*b^4*c^3+775200*a^14*b^3*c^3+155040*a^15*b^2*c^3 +19380*a^16*b*c^3+1140*a^17*c^3+190*b^18*c^2+3420*a*b^17*c^2 +29070*a^2*b^16*c^2+155040*a^3*b^15*c^2+581400*a^4*b^14*c^2 +1627920*a^5*b^13*c^2+3527160*a^6*b^12*c^2+6046560*a^7*b^11*c^2 +8314020*a^8*b^10*c^2+9237800*a^9*b^9*c^2+8314020*a^10*b^8*c^2 +6046560*a^11*b^7*c^2+3527160*a^12*b^6*c^2+1627920*a^13*b^5*c^2 +581400*a^14*b^4*c^2+155040*a^15*b^3*c^2+29070*a^16*b^2*c^2 +3420*a^17*b*c^2+190*a^18*c^2+20*b^19*c+380*a*b^18*c+3420*a^2*b^17*c +19380*a^3*b^16*c+77520*a^4*b^15*c+232560*a^5*b^14*c+542640*a^6*b^13*c +1007760*a^7*b^12*c+1511640*a^8*b^11*c+1847560*a^9*b^10*c +1847560*a^10*b^9*c+1511640*a^11*b^8*c+1007760*a^12*b^7*c +542640*a^13*b^6*c+232560*a^14*b^5*c+77520*a^15*b^4*c+19380*a^16*b^3*c +3420*a^17*b^2*c+380*a^18*b*c+20*a^19*c+b^20+20*a*b^19+190*a^2*b^18 +1140*a^3*b^17+4845*a^4*b^16+15504*a^5*b^15+38760*a^6*b^14 +77520*a^7*b^13+125970*a^8*b^12+167960*a^9*b^11+184756*a^10*b^10 +167960*a^11*b^9+125970*a^12*b^8+77520*a^13*b^7+38760*a^14*b^6 +15504*a^15*b^5+4845*a^16*b^4+1140*a^17*b^3+190*a^18*b^2+20*a^19*b+a^20 <『Maxima』の使い方> 例えば、(a+b)^50 を展開させる場合 expand((a+b)^50) と全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【問題3 】 高次方程式 x^3+2x^2+2x+1=0 を解きなさい。 |
| 高校で扱う高次方程式は因数定理などを利用して因数分解するか、または、x^2=t と置いて解ける形のものになっている。 「高次方程式」の指導の導入で、2次方程式に解の公式があったように、3次方程式にも解の公式があることを『Maxima』に ax^3+bx^2+cx+d=0 を解かせて提示したら、生徒たちに驚きや感動を与えられる授業ができないだろうか。 また、3次方程式 x^3-6x-10=0、4次方程式 x^4+3x^3-18x^2+6x-5=0 を『Maxima』に解かせて提示したならばその解の複雑さに生徒たちは驚きを感じるはずである。 <『Maxima』の使い方> 例えば、 ax^3+bx^2+cx+d=0 を解かせる場合 solve(a*x^3+b*x^2+c*x+d=0,x) と全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 3次方程式 ax^3+bx^2+cx+d=0 を『Maxima』に解かせた結果 |
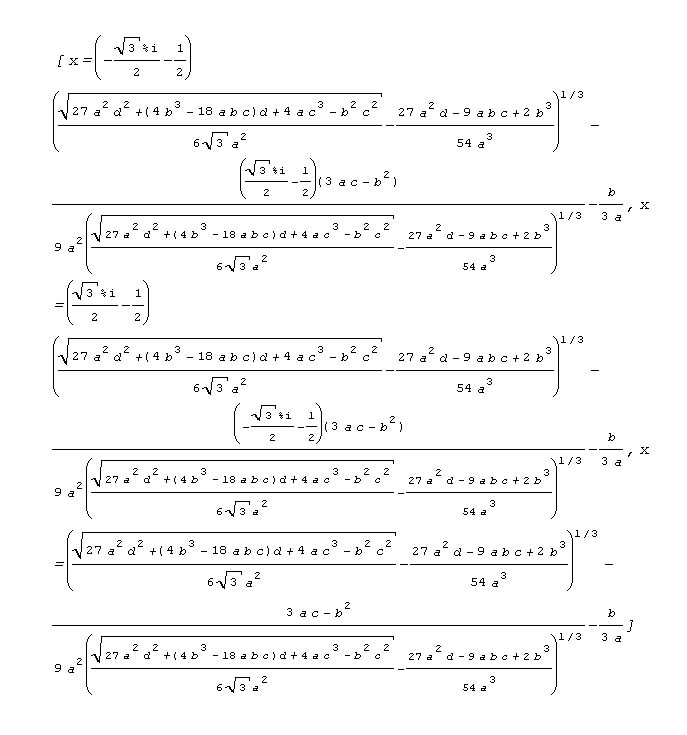 |
| 3次方程式 x^3-6x-10=0 を『Maxima』に解かせた結果 |
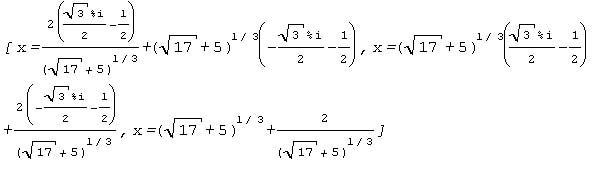 |
| 【問題4】 ab-a+b-1 を因数分解しなさい。 |
| これは1つの文字に整理して因数分解する問題である。 もっと複雑な因数分解を『Maxima』にさせて提示したら、生徒たちに驚きや感動を与えられる授業ができないだろうか。 (a+b+c)(bc+ca+ab)-abc、(b-c)^3+(c-a)^3+(a-b)^3、a^3+b^3+c^3-3abc、(b+c)(c+a)(a+b)+abc を『Maxima』に瞬時に因数分解せて提示したならば生徒たちは驚きを感じるはずである。 以下、『Maxima』に因数分解させた結果である。 (a+b+c)(bc+ca+ab)-abc = (b+a)(c+a)(c+b) (b-c)^3+(c-a)^3+(a-b)^3 = 3(b-a)(c-a)(c-b) a^3+b^3+c^3-3*a*b*c = (c+b+a)(c^2-b*c-a*c+b^2-a*b+a^2) (b+c)(c+a)(a+b)+abc = (c+b+a)(bc+ac+ab) <『Maxima』の使い方> 例えば、(a+b+c)(bc+ca+ab)-abc を因数分解させる場合 factor((a+b+c)*(b*c+c*a+a*b)-a*b*c) と全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【問題5】 (x+7x^2)^(1/3) を微分しなさい。 |
| 問題集などでもっと複雑な式を探して、『Maxima』に微分させて提示したら、生徒たちに驚きや感動を与えられる授業ができないだろうか。 以下、『Maxima』に微分させた結果である。 {(x+7x^2)^(1/3)}’ = (14*x+1)/(3*(7*x^2+x)^(2/3)) <『Maxima』の使い方> 例えば、(x+7x^2)^(1/3) を微分させる場合 diff((x+7*x^2)^(1/3), x) と全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 【問題6】 √1+5x を積分しなさい。 |
| 問題集などでもっと複雑な式を探して、『Maxima』に積分させて提示したら、生徒たちに驚きや感動を与えられる授業ができないだろうか。 以下、『Maxima』に積分させた結果である。 ∫√(1+5x)dx = (2*(5*x+1)^(3/2))/15 <『Maxima』の使い方> 例えば、 √1+5x を積分させる場合 integrate(sqrt(1+5*x) , x) と全て半角で入力し、 Shiftキー と Enterキー を同時に押す。 |
| 数式処理ソフト『Maxima』 | 数式処理ソフト『wxMaxima』 |
| 上の 数式処理ソフト『wxMaxima] をクリックすると、Maxima公式サイトが開く。 このMaxima公式サイトの左のメニューから Download をクリックする。 次に、Sourceforge download page をクリックする。 そして、Maxima Windows をクリックする。 更に、5.26.0-Windows をクリックする。 続いて、maxima-5.26.0.exe をクリックすると、『maxima 5.26.0.exe』がダウンロードされる。 ダウンロードされた 『maxima-5.26.0.exe』 をダブルクリックして『Maxima』のインストーラを起動する。 以後は、画面の表示に従ってインストールを行う。ただし、『maxima-5.26.0.exe』の5.26.0はバージョンを表す。(2012/02/12現在) |
| デスクトップに、「wxMaxima」のアイコンができているので、それをダブルクリックして『Maxima』を起動する。 |
| このwebページで表示した全てのサンプルを納めたMaximaのデータファイル「MSamp.wxm」をダウンロードできます。 下の[データファイル「MSamp.lzh」]をクリックして、デスクトップ等に保存してください。 ダウンロードしたファイル「MSamp.lzh」を解凍して、実行したい入力式にカーソルを置いて、Shifeキー と Enterキー を同時に押すと実行できます。もちろん、その前に、「Maxima」がインストールされていなければなりません。 |
| データファイル「MSamp.wxm」 |