 |
 |
| LastUpdate 6/22/2024 |
| @My first encounter with computers was during a university lecture. It
was a lecture on how to write a programing language called "Fortran".
I remember punching holes in a peace of paper tape and letting a big computer
read the program I created. @In my first year as a teacher , I encountered a computer called "NEC-PC9801" at the school where I worked. As a strage medium , I inserted a 5-inch floppy disk , which I think is quite large , into the main unit. @By the way , the strage medium of the personal computer I purchased for home use was a casstte tape. It wasn't just for personal computers. It was for cassette tape recorders that are still around today for listening to and memorizing music. The boot program is also included in this cassette tape , and it takes about 5 minutes for the computer to start up. @At that time , computers were machines for numerical processing and could not process mathematical formulas. However , computers now calculate not only numbers , but also formulas. If you use formula manipulation software , "organize formulas" , "expand" , "factorize" , "solve linear equation" , "solve quadratic equations" , "solve cubic equations" , "solve quartic equations" , " differentiate" , and "Integration" is easy for you to do. @Three-dimensional graphs can be easily drawn using Maxima. By dragging the graph , you can freely change the viewing direction of the graph. @Typical formula manipulation software includes (1) "Mathematica" , (2) "Maple" , and (3) "Maxima". While (1) , (2) are expensive , ranging from 200,000 yen to 300,000 yen , (3) "Maxima" is free software, so it is free. @In addition , the source code of "Maxima "is open to the public (open source) , and all kinds of people around the world volunteer to participate in its development. "Maxima" is written in a programming language called "LISP". @In addition , "wxMaxima 0.8.7"was used for the following examples. |
| @yExample 1z@Draw a graph of a 3D explicit function. mMexican hatn |
mPnFunction expression @@@ mQnInput formula @plot3d(sin(sqrt(x^2+y^2))/sqrt(x^2+y^2),[x,-3*%pi,3*%pi],[y,-3*%pi,3*%pi],[plot_format,gnuplot],[grid,50,50]); mRnDrawing result @@@@@ 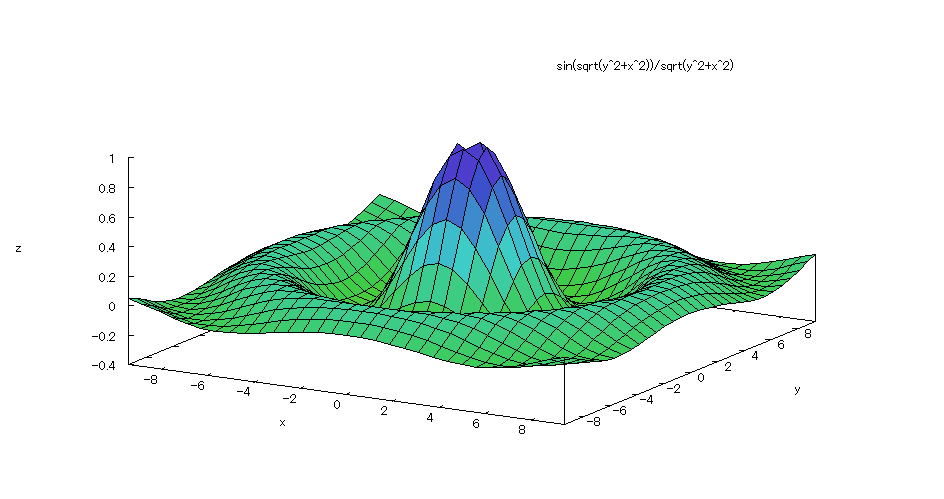 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 2z@Draw a graph of a 3D explicit function. mCaldera shapen |
mPnFunction expression @@@ mQnInput formula @@@plot3d(exp(-(x^2+y^2)/2)*(x^2+y^2)/(2*%pi),[x,-2,2],[y,-2,2],[plot_format,gnuplot],[grid,50,50]); mRnDrawing result @@@@@ 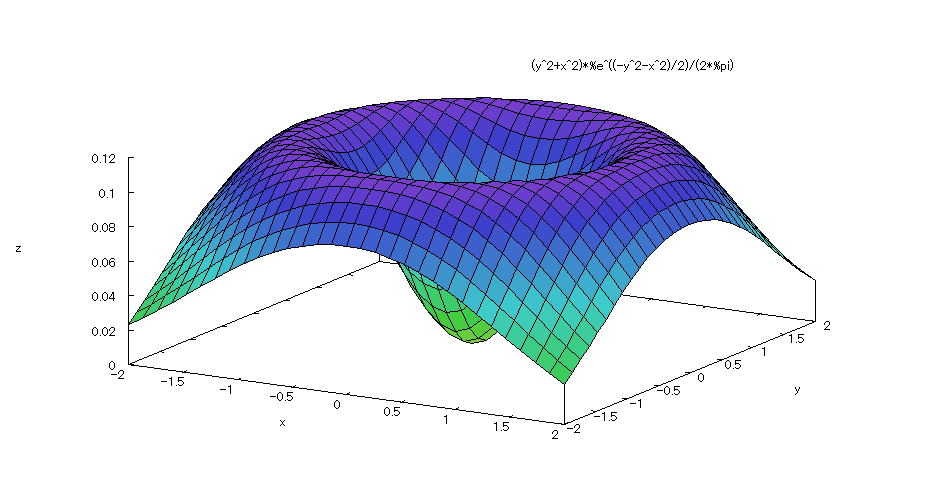 How to draw a graph @ As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 3z@Draw a graph of a 3D explicit function. mA slightly sunken saddle shapen |
mPnFunction expression @@@ mQnInput formula @@@plot3d(3*exp(-(x^2+y^2))*(2*x^2+y^2),[x,-2,2],[y,-2,2],[plot_format,gnuplot],[grid,50,50]); mRnDrawing result @@@@@ 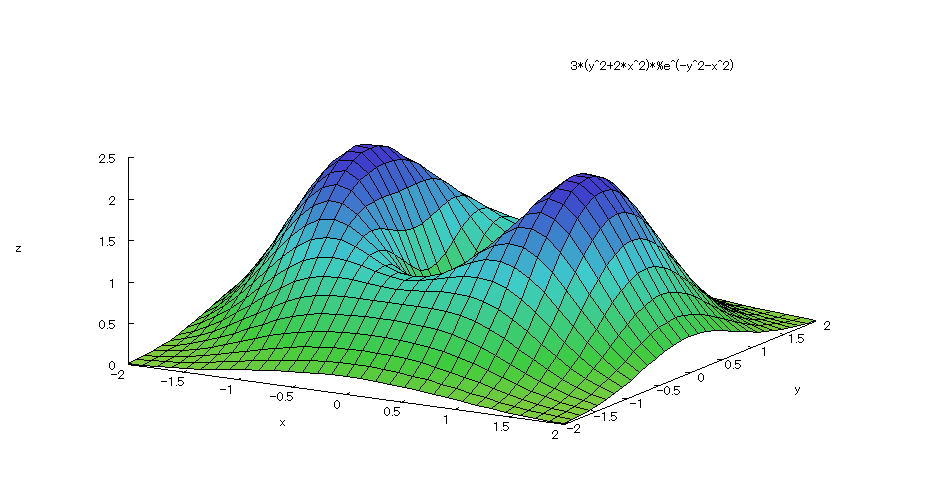 How to draw a graph @ As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 4z@Draw a wireframe graph of a 3D implicit function. mSpheren |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2+y^2+z^2=1,x,-1,1,y,-1,1,z,-1,1)); mRnDrawing result @@@@@ 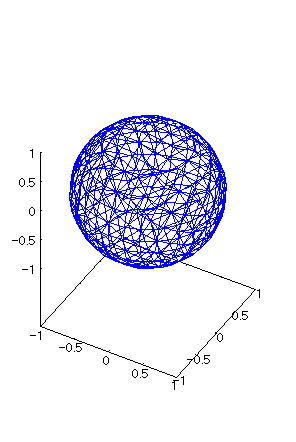 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 5z@Draw a graph of a 3D implicit function with hidden surface processing. mSpheren |
mPnFunction expression @@@ mQnInput formula @@@draw3d(enhanced3d=true,implicit(x^2+y^2+z^2=1,x,-1,1,y,-1,1,z,-1,1)); mRnDrawing result @@@@@ 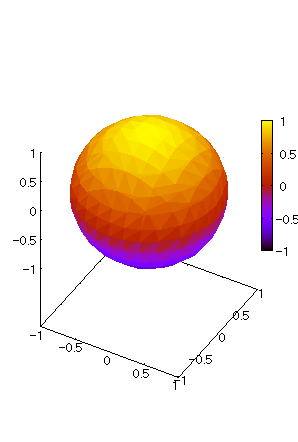 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 6z Draw a graph of a 3D implicit function with hidden surface processing. mHollow drumn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(enhanced3d=true,implicit(x^2+y^2-z^2=1,x,-2,2,y,-2,2,z,-2,2)); mRnDrawing result @@@@@ 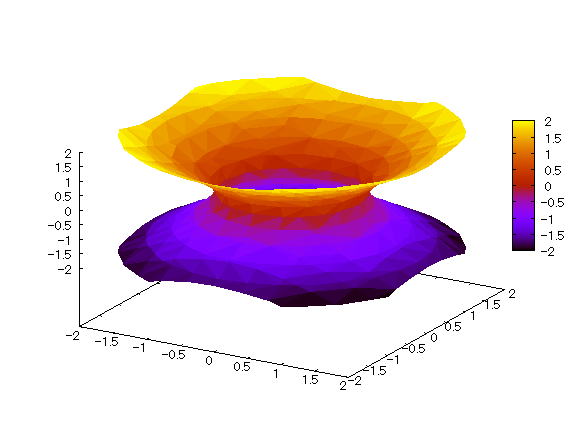 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 7z Draw a graph of a 3D implicit function with hidden surface processing. mSewer pipe jointn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(enhanced3d=true,implicit((x^2-1)^2+(y^2-1)^2+(z^2-1)^2=1.5, x,-1,1,y,-1,1,z,-1,1)); mRnDrawing result @@@@@ 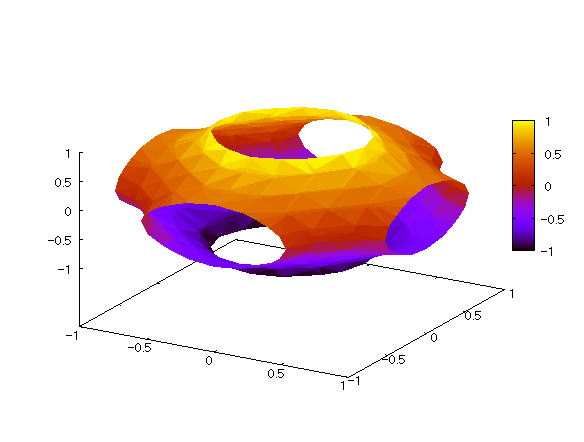 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 8z@Draw a graph of a 3D implicit function with hidden surface processing. ma cell with nucleus in the centern |
mPnFunction expression @@@({Ó){(|Ó) {({Ó){(|Ó){({Ó){(|Ó)Q @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@iHowever , Ó represents the golden ratio.j mQnInput formula @@@draw3d(enhanced3d=true,implicit(cos(x+%phi*y)+cos(x-%phi*y)+cos(y+%phi*z) @@@@@@@@@@@@@@@@@+cos(y-%phi*z)+cos(z+%phi*x)+cos(z-%phi*x)=2,x,-4,4,y,-4,4,z,-4,4)); mRnDrawing result @@@@@ 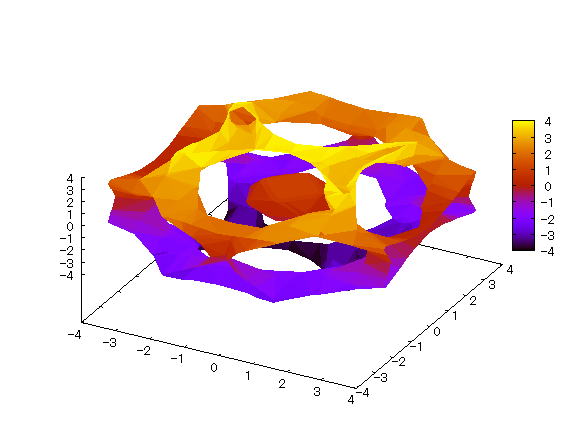 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 9z@Draw a graph of a 3D parameter. mSpheren |
mPnFunction expression @@@E @@@E @@@@@@@@@@@iO QÎj iO Îj mQnInput formula @@@plot3d([cos(s)*cos(t),cos(s)*sin(t),sin(s)],[s,0,2*%pi],[t,0,%pi]); mRnDrawing result @@@@@ 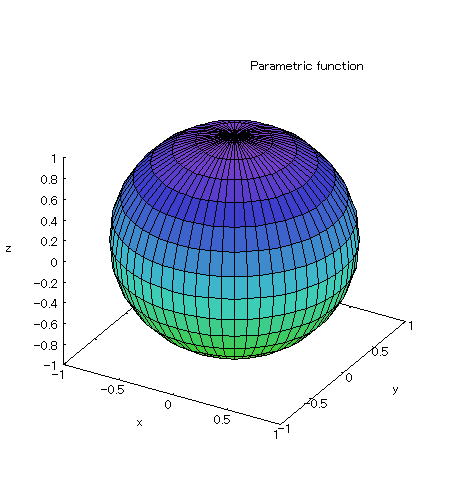 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 10z@Draw a graph of a 3D parameter. mDonut shapeitorusjn |
mPnFunction expression @@@(T{Q) @@@(T{Q) @@@Q @@@@@@@@@@@iO QÎj iO QÎj mQnInput formula @@@plot3d([(5+2*cos(s))*cos(t),(5+2*cos(s))*sin(t),2*sin(s)],[s,0,2*%pi],[t,0,2*%pi]); mRnDrawing result @@@@@ 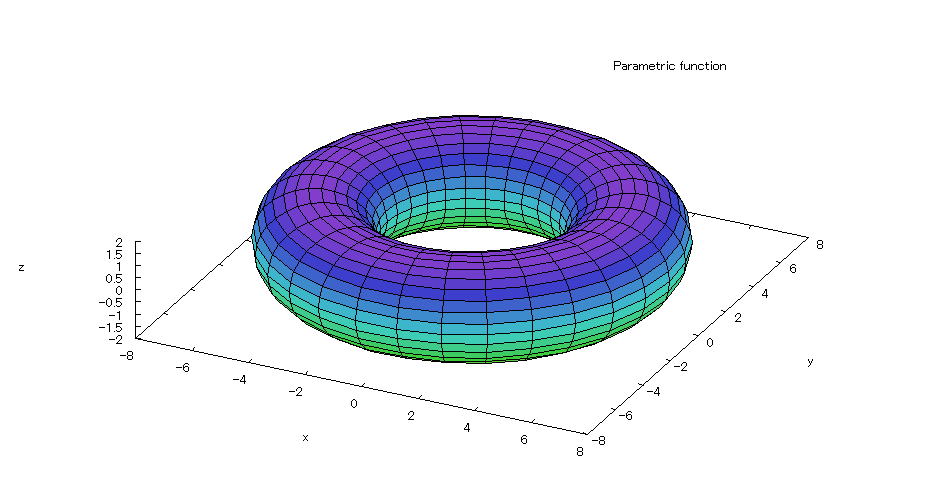 How to draw a graph @ As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 11z@Draw a graph of a 3D parameter mSpring typen |
mPnFunction expression @@@(T{) @@@(T{) @@@{ODU @@@@@iO QÎj iO VÎj mQnInput formula @@@plot3d([(5+cos(s))*cos(t),(5+cos(s))*sin(t),sin(s)+0.6*t],[s,0,2*%pi],[t,0,7*%pi]); mRnDrawing result @@@@@ 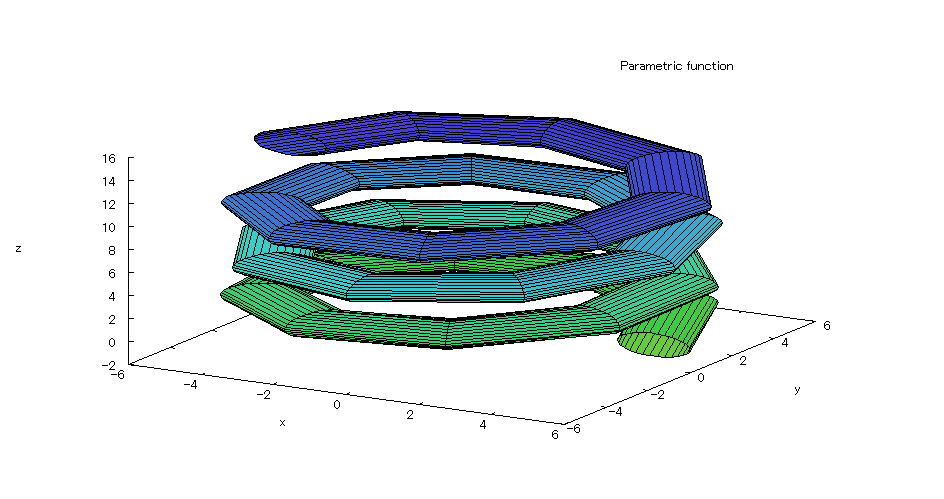 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 12z@Draw a graph of a 3D parameter. mMobius stripn |
mPnFunction expression @@@ @@@ @@@ mQnInput formula @@@plot3d([cos(s)*(3+t*cos(s/2)),sin(s)*(3+t*cos(s/2)),t*sin(s/2)],[s,0-%pi,%pi],[t,-1,1]); mRnDrawing result @@@@@ 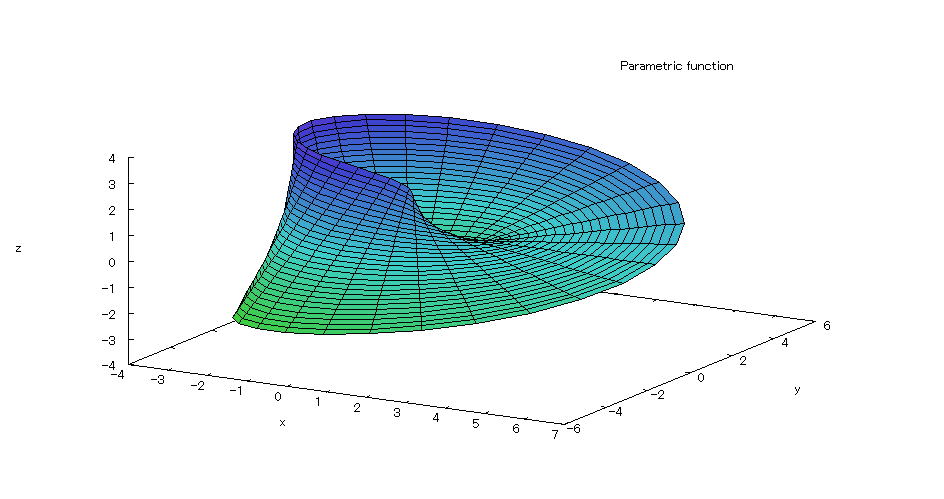 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 13z@Draw a graph of a 3D parameter. mKlein's jarn |
mPnFunction expression @@@ @@@ @@@ @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@i|Î Îj i|Î Îj mQnInput formula @@@plot3d([5*cos(s)*(cos(s/2)*cos(t)+sin(s/2)*sin(2*t)+3)-10, @@@@-5*sin(s)*(cos(s/2)*cos(t)+sin(s/2)*sin(2*t)+3.0),5*(-sin(s/2)*cos(t)+cos(s/2)*sin(2*t))], @@@@@[s,-%pi,%pi],[t,-%pi,%pi]); mRnDrawing result @@@@@ 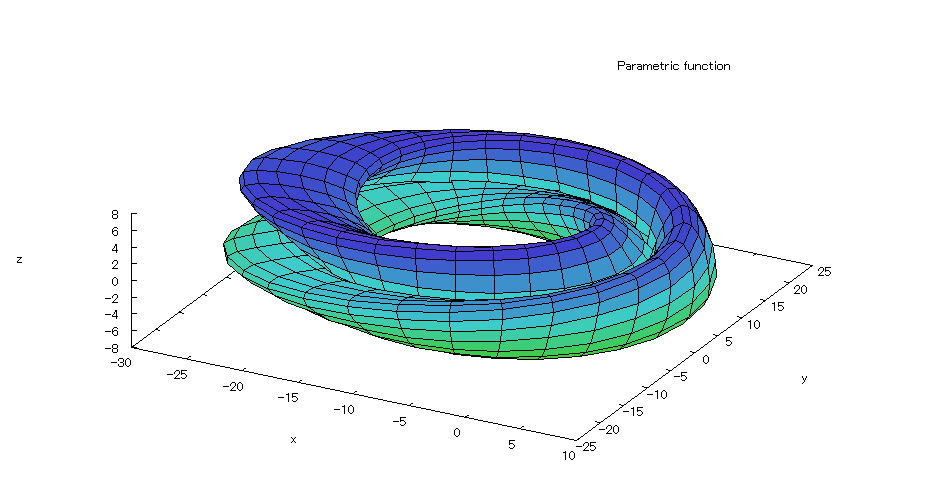 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample14z@Draw a graph of a 2D explicit function. mQuadratic functionn |
mPnFunction expression @@@ mQnInput formula @@@ plot2d(3*x^2-1,[x,-2,2]); mRnDrawing result @@@@@ 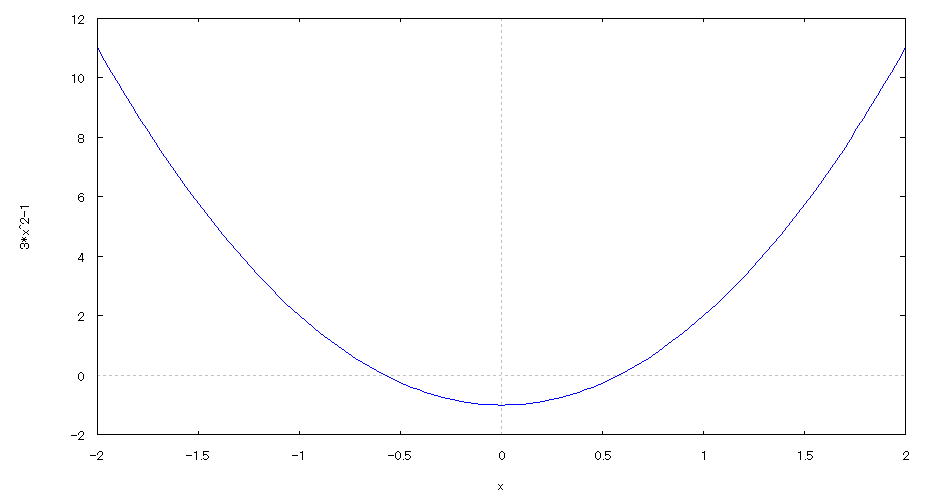 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 15z@Draw a graph of a 2D explicit function. mExpotentialETrigonometric functionn |
mPnFunction expression @@@@ mQnInput formula @@@ plot2d(exp(x)*sin(7*x),[x,0,20]); mRnDrawing result @@@@@ 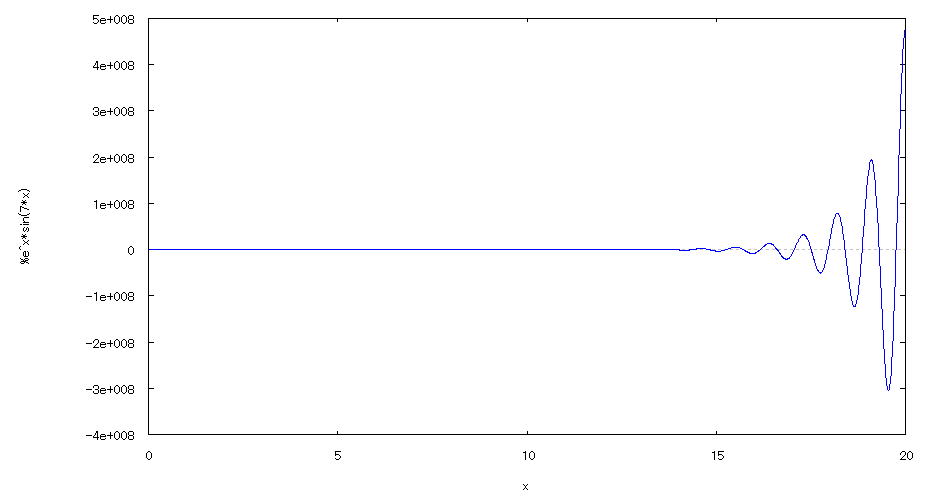 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 16z@Draw a graph of a 2D explicit function. mDraw multiple graphs simultaneouslyn |
mPnFunction expression @@@@@AQAR@@@iO QÎj mQnInput formula @@@ plot2d([sin(x),sin(2*x),sin(3*x)],[x,0,2*%pi]); mRnDrawing result @@@@@ 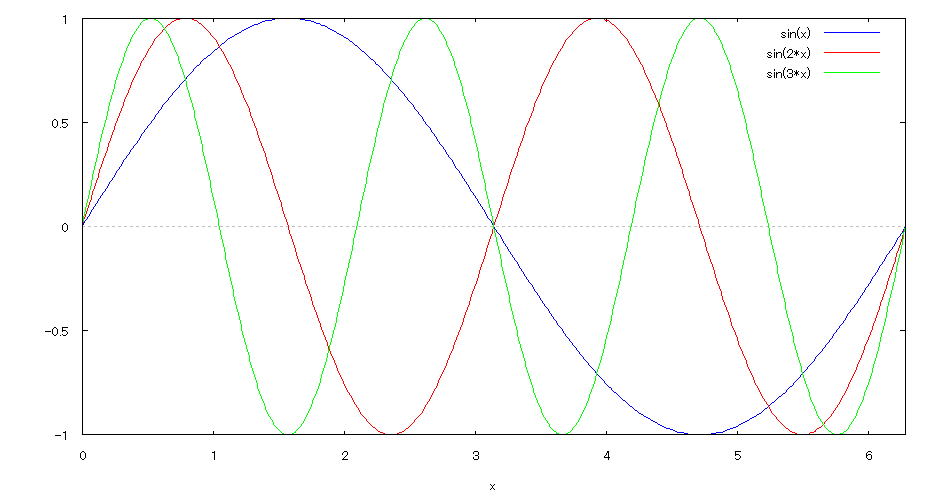 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 17z@Draw a graph of a 2D implicit function. mCirclen |
mPnFunction expression @@@@ mQnInput formula @@@ implicit_plot(x^2+y^2=1,[x,-2,2],[y,-2,2]); mRnDrawing result @@@@@ 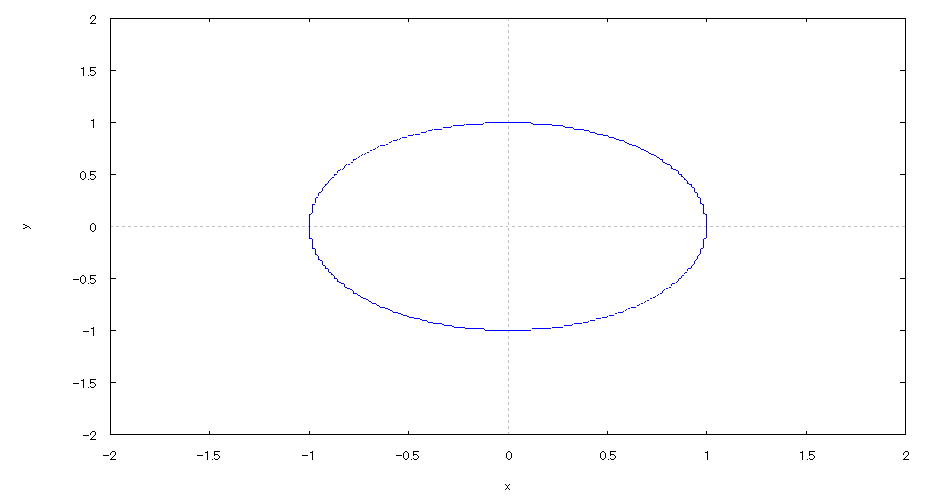 How to draw a graph @First , input "load(implicitplot)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 18z@Draw a graph of a 2D implicit function. mFour leaf clovern |
mPnFunction expression @@@@ @@@ mQnInput formula @@@ implicit_plot((x^2+y^2)^4-(x^2-y^2)^2=0,[x,-2,2],[y,-2,2]); mRnDrawing result @@@@@ 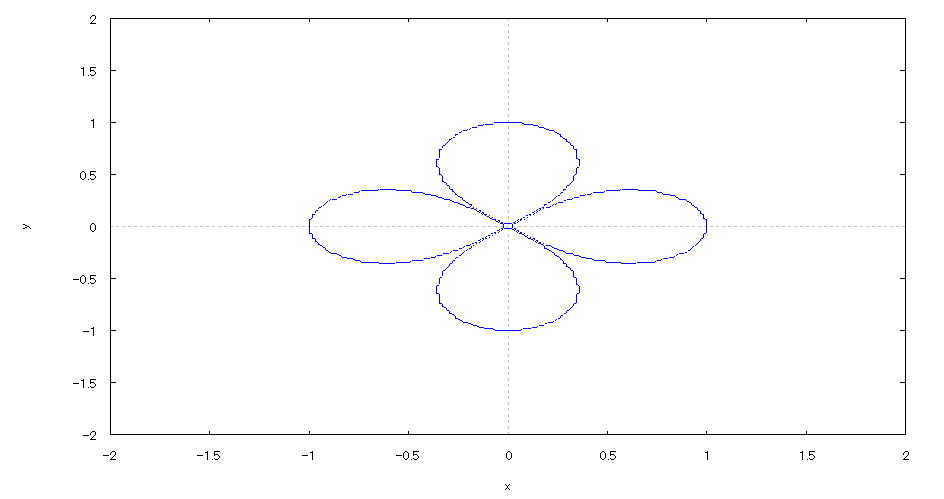 How to draw a graph @First , input "load(implicitplot)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 19z@Draw a graph of a 2D implicit function. mCircle and Four leaf clovern |
mPnFunction expression @@@@ @@@@ mQnInput formula @@@ plot2d([x^2+y^2=1,(x^2+y^2)^4-(x^2-y^2)^2=0],[x,-2,2],[y,-2,2]); mRnDrawing result @@@@@ 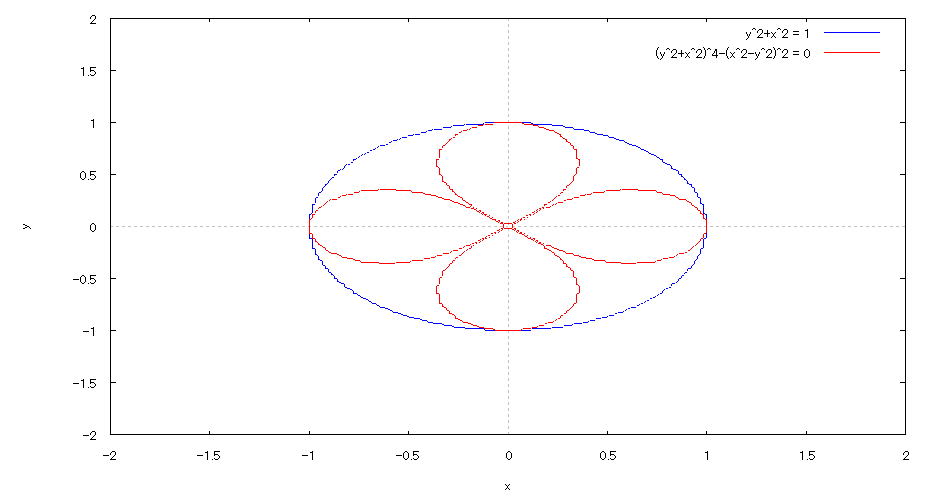 How to draw a graph @First , input "load(implicitplot)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 20z@Draw a graph of a 2D parameter. m shapen |
mPnFunction expression @@@@ @@@@Q @iO QÎj POO divisions mQnInput formula @@@ plot2d([parametric,cos(t),sin(2*t)],[t,0,2*%pi],[nticks,100]); mRnDrawing result @@@@@ 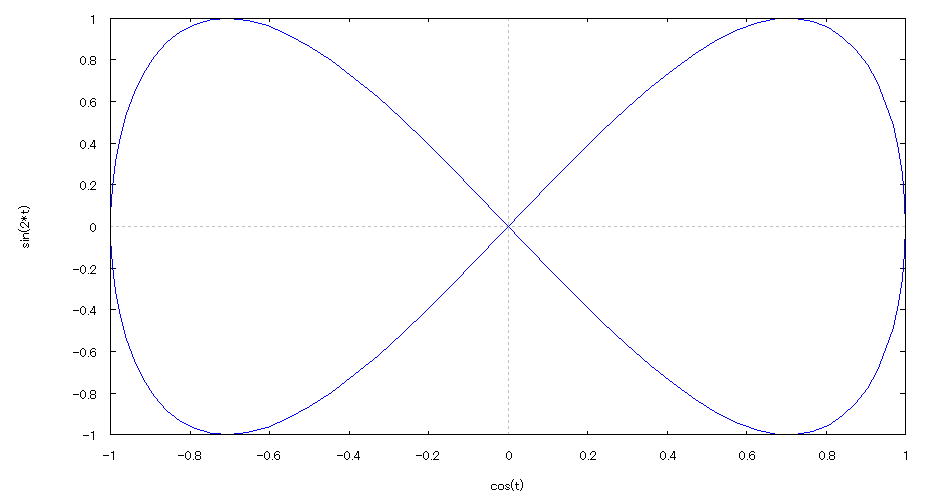 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 21z@Draw a graph of a 2D parameter. mChrysanthemum petal shapen |
mPnFunction expression @@@@SS @@@@SS @iO QÎj@ SOO divisions mQnInput formula @@@ plot2d([parametric,4*sin(4*t)*cos(t),4*sin(4*t)*sin(t)],[t,0,2*%pi],[nticks,400]); mRnDrawing result @@@@@ 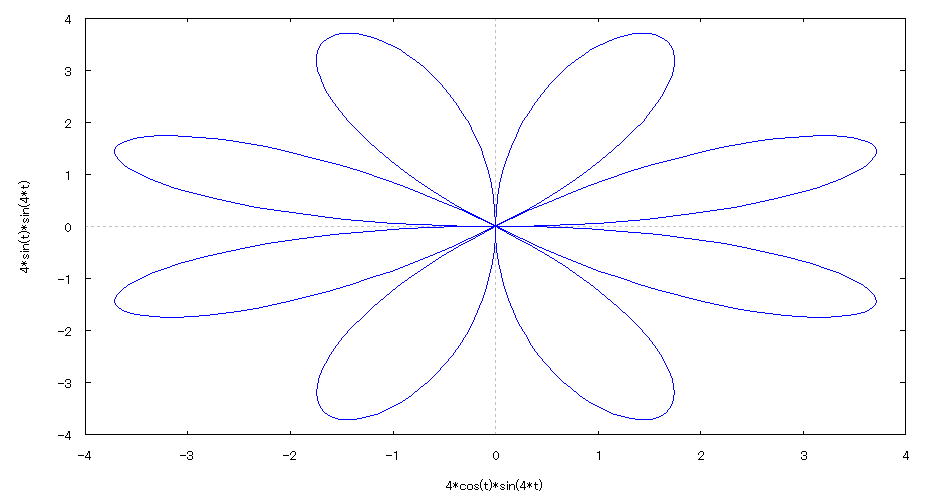 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 22z@Draw a graph of a 2D parameter. mSwirl shapen |
mPnFunction expression @@@@@@@@ @ @@@@ @@@@@ mQnInput formula @@@ plot2d([parametric,t*cos(t),t*sin(t)],[t,0,35*%pi/2],[nticks,500]); mRnDrawing result @@@@@ 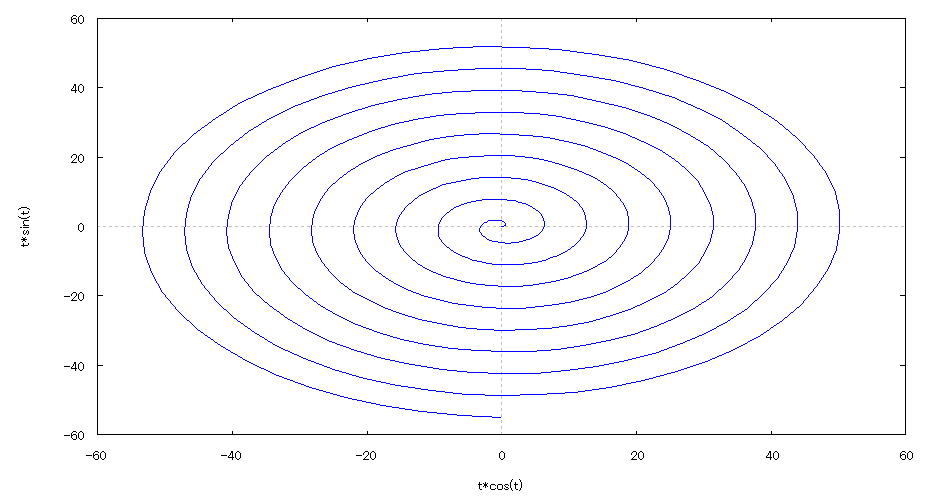 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 23z@Draw a graph of a 2D parameter. mHeart shapen |
mPnFunction expression @@@@(P{) @@@@(P{) @@iO QÎj@ POO divisions mQnInput formula @@@ plot2d([parametric,(1+cos(t))*cos(t),(1+cos(t))*sin(t)],[t,0,2*%pi],[nticks,100]); mRnDrawing result @@@@@ 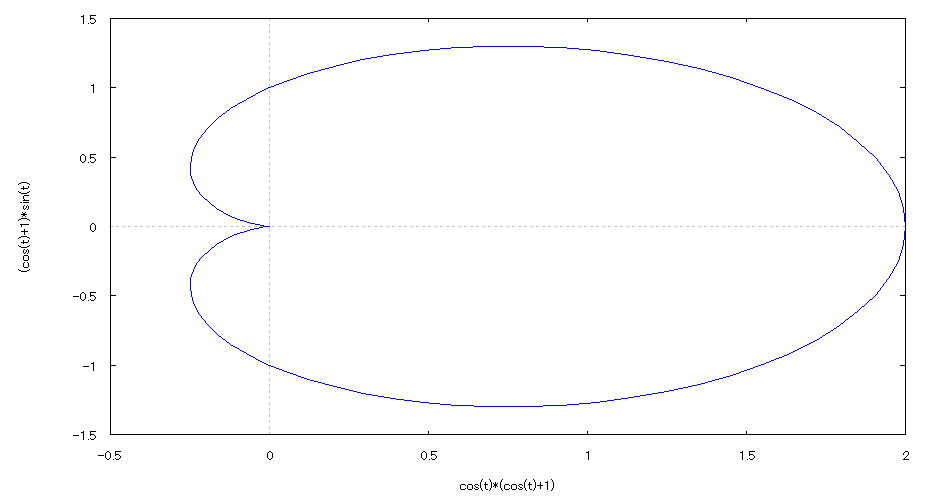 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 24z@Draw a wireframe graph of a 3D implicit function. mellipsoidn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/1^2+y^2/2^2+z^2/3^2=1,x,-1,1,y,-2,2,z,-3,3)); @@@ mRnDrawing result @@@@@ 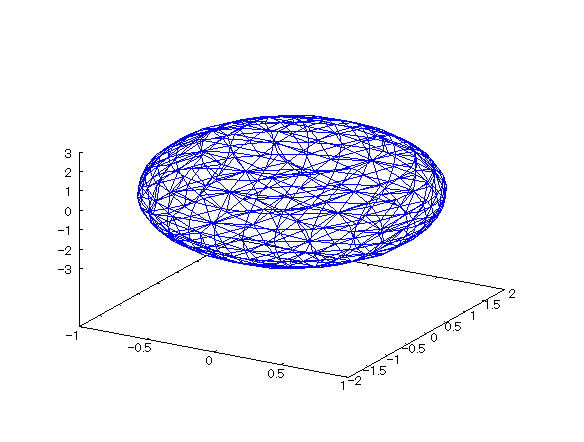 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 25z@Draw a wireframe graph of a 3D implicit function. mSingle leaf hyperbolan |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/1^2+y^2/2^2-z^2/3^2=1,x,-7,7,y,-7,7,z,-7,7)); @@@ mRnDrawing result @@@@@ 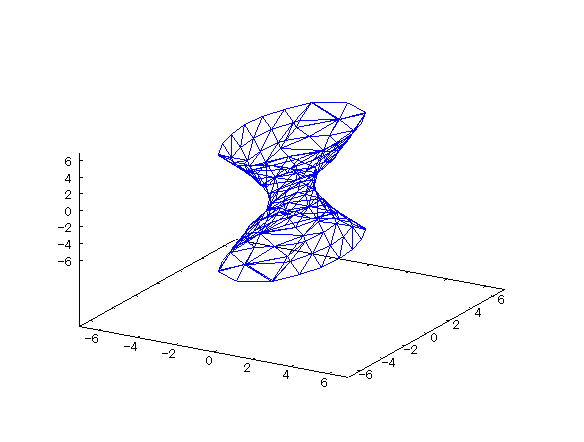 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 26z@Draw a wireframe graph of a 3D implicit function. mBilobal hyperbolan |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/1^2-y^2/2^2-z^2/3^2=1,x,-2,2,y,-4,4,z,-8,8)); @@@ mRnDrawing result @@@@@ 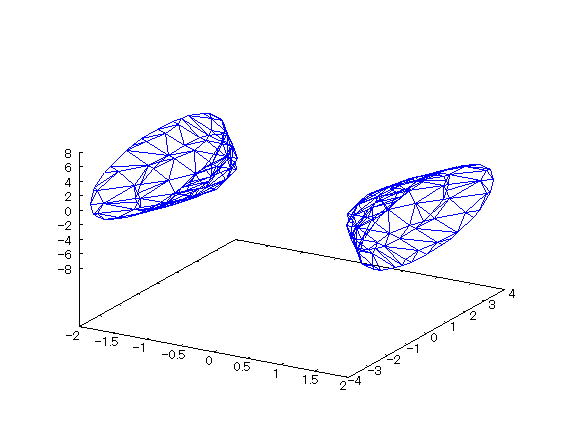 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 27z@Draw a wireframe graph of a 3D implicit function. mElliptical paraboloidn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/1^2+y^2/2^2=1/20*z,x,-1,1,y,-2,2,z,0,20)); @@@ mRnDrawing result @@@@@ 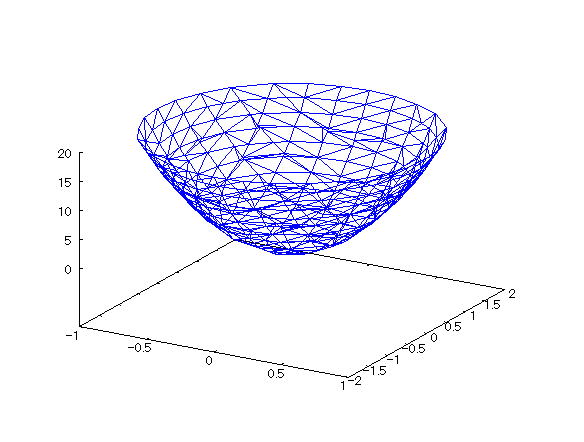 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 28z@Draw a wireframe graph of a 3D implicit function. mHyperbolic paraboloidn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/1^2-y^2/2^2=1/2*z,x,-2,2,y,-3,3,z,-4,4)); @@@ mRnDrawing result @@@@@ 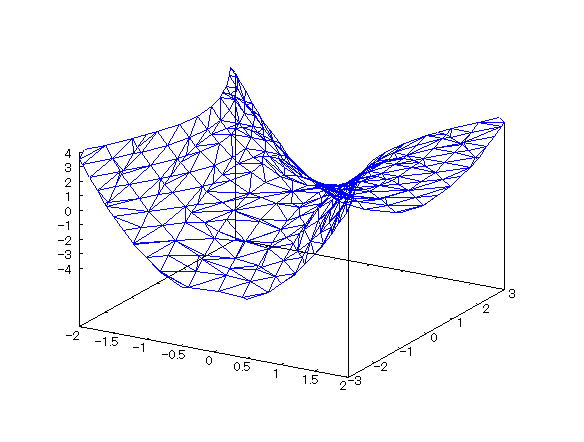 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 29z@Draw a wireframe graph of a 3D implicit function. mElliptical cylindern |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/1^2+y^2/2^2=1,x,-2,2,y,-2,2,z,-10,10)); @@@ mRnDrawing result @@@@@ 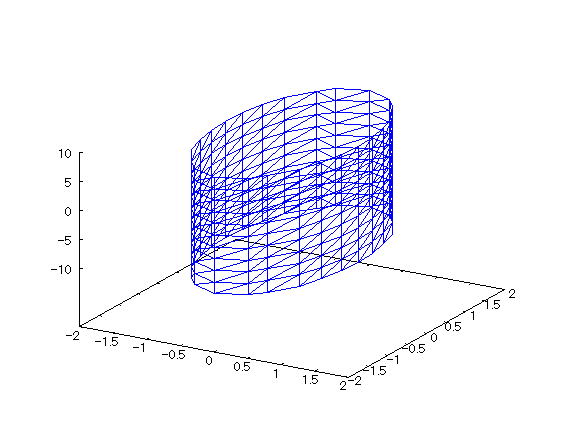 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 30z@Draw a wireframe graph of a 3D implicit function. mHyperbolic columnn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2/2^2-y^2/3^2=1,x,-10,10,y,-10,10,z,-20,20)); @@@ mRnDrawing result @@@@@ 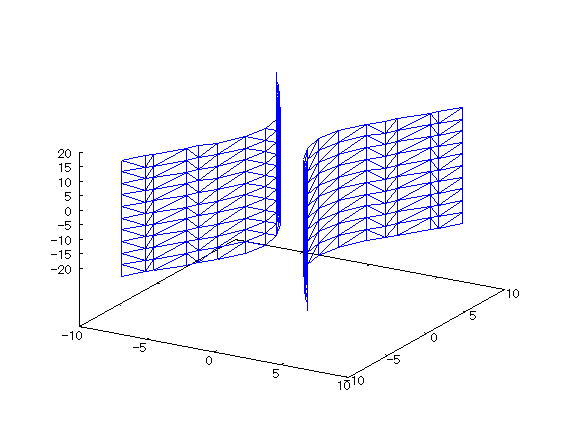 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 31z@Draw a wireframe graph of a 3D implicit function. mParabolic columnn |
mPnFunction expression @@@ mQnInput formula @@@draw3d(implicit(x^2=y,x,-5,5,y,0,25,z,-20,20)); @@@ mRnDrawing result @@@@@ 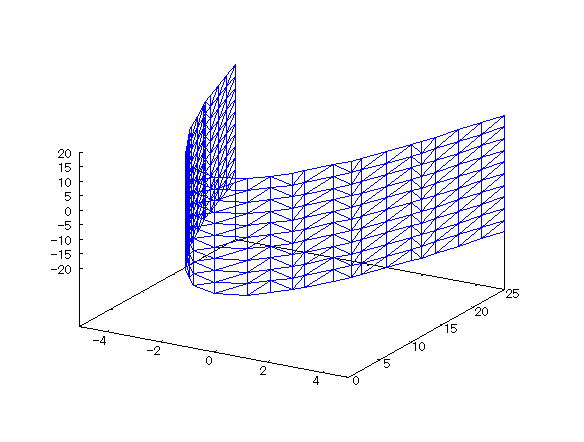 How to draw a graph @First , input "load(draw)" and press the Shift key and Enter key at the same time to load the package. @Next , as in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 32z@Draw a graph of a 2D explicit function. mMake it easier to see by specifying the range of y valuesn |
mPnFunction expression @@@ mQnInput formula @@@plot2d((x^3+2*x^2-4*x-3)/(x+1),[x,-3,3],[y,-10,10]); @@@ mRnDrawing result @@@@@ 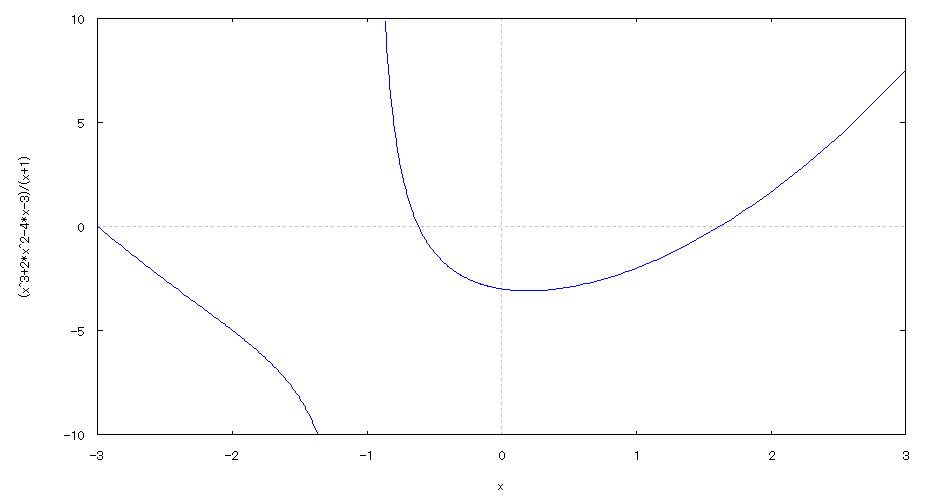 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 33z@Draw a graph of a 2D explicit function. mDisplay multiple graphs simultaneouslyn |
mPnFunction expression @@@ mQnInput formula @@@plot2d([exp(-2*x),exp(x),1],[x,-2,2],[y,0,10]); @@@ mRnDrawing result @@@@@ 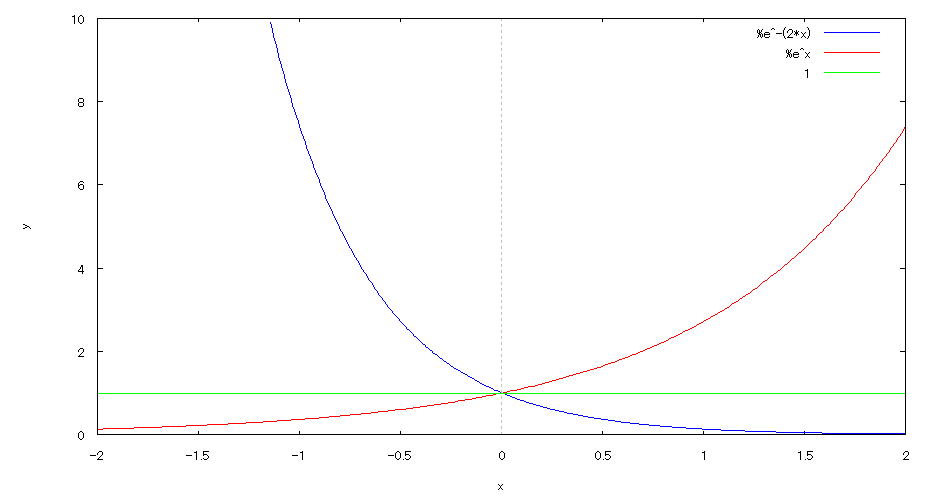 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 34z@Draw a graph of a 2D explicit function. mFind the number of real solutions to an equationn |
mPnEquation @@@ mQnInput formula @@@plot2d([x/8,cos(x)],[x,-15,15],[y,-2,2]); @@@ mRnDrawing result @@@@@ 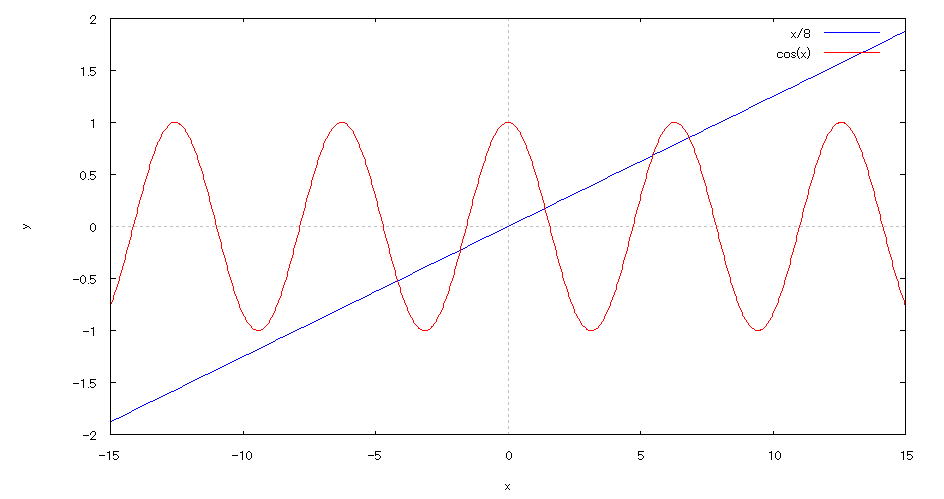 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @Since there are 5 intersections , we know that the equation has 5 real solutions. @ |
| @yExample 35z@Draw a graph of a 2D parameter. mSpecify the number of divisionsn |
mPnFunction expression @@@ mQnInput formula @@@plot2d([parametric,3*cos(t)+cos(13*t),3*sin(t)+sin(13*t)],[t,0,2*%pi],[nticks,300]); @@@ mRnDrawing result @@@@@ 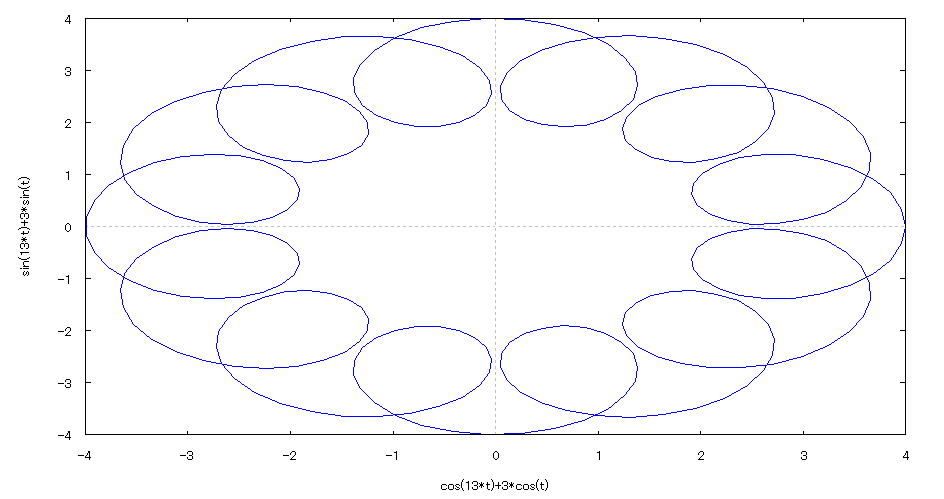 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 36z@Draw a graph of a 2D parameter. mLissajous curven |
mPnFunction expression @@@ mQnInput formula @@@plot2d([parametric,cos(7*t),sin(4*t)],[t,0,2*%pi],[nticks,300]); @@@ mRnDrawing result @@@@@ 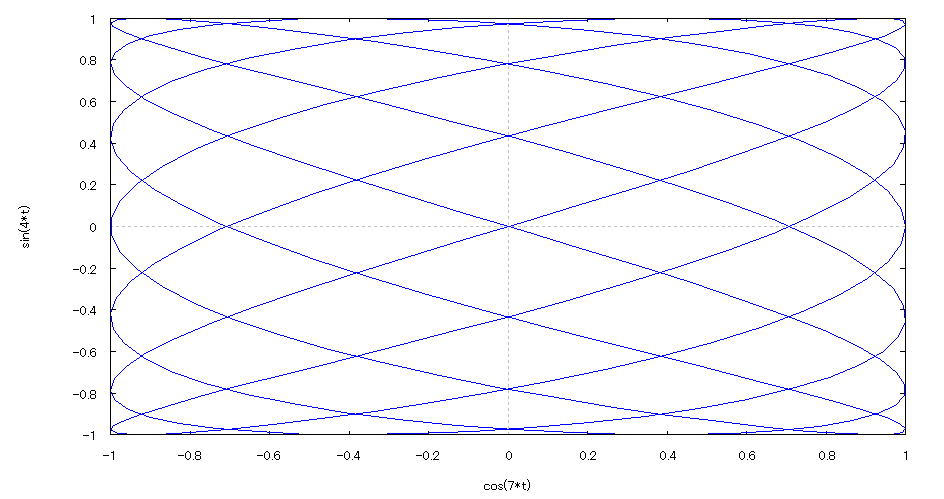 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 37z@Draw a graph of a 2D parameter. mBernoulli's lemniscate curven |
mPnFunction expression @@@ mQnInput formula @@@plot2d([parametric,cos(t)/(1+sin(t)^2),sin(t)*cos(t)/(1+sin(t)^2)],[t,0,2*%pi],[nticks,300]); @@@ mRnDrawing result @@@@@ 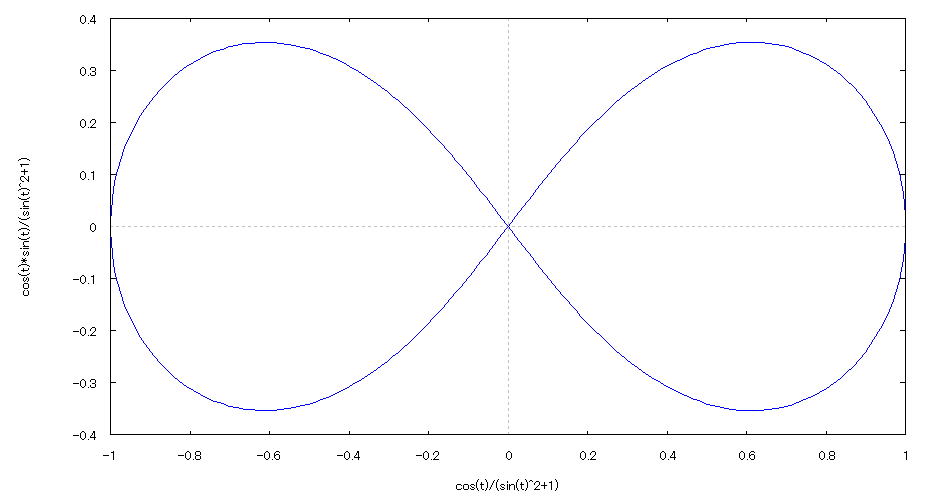 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 38z@Draw a graph of a 3D explicit function. mDo not specify the number of devisionsn |
mPnFunction expression @@@ mQnInput formula @@@plot3d(exp(-sqrt(x^2+y^2)/2)*cos(%pi*sqrt(x^2+y^2)),[x,-4,4],[y,-4,4]); @@@ mRnDrawing result @@@@@ 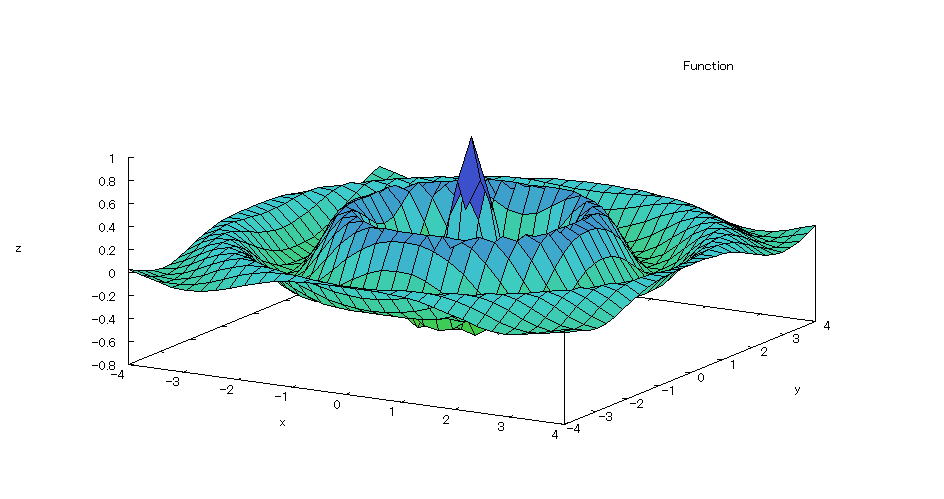 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 39z@Draw a graph of a 3D explicit function. mShark minimal surfacen |
mPnFunction expression @@@ mQnInput formula @@@plot3d(log(cos(x)/cos(y)),[x,-%pi/2,%pi/2],[y,-%pi/2,%pi/2]); @@@ mRnDrawing result @@@@@  How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 40z@Draw a graph of a 3D explicit function. mDefine and draw a functionn |
mPnFunction expression @@@@@ 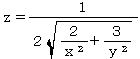 @@@iO
QCO
Qj @@@iO
QCO
QjmQnInput formula @@@u(a,x,y,p,q,r):=a*(p*x^(-r)+q*y^(-r))^(-1/r); @@@plot3d(u(2,x,y,2,3,2),[x,0.01,2],[y,0.01,2]); @@@ mRnDrawing result @@@@@ 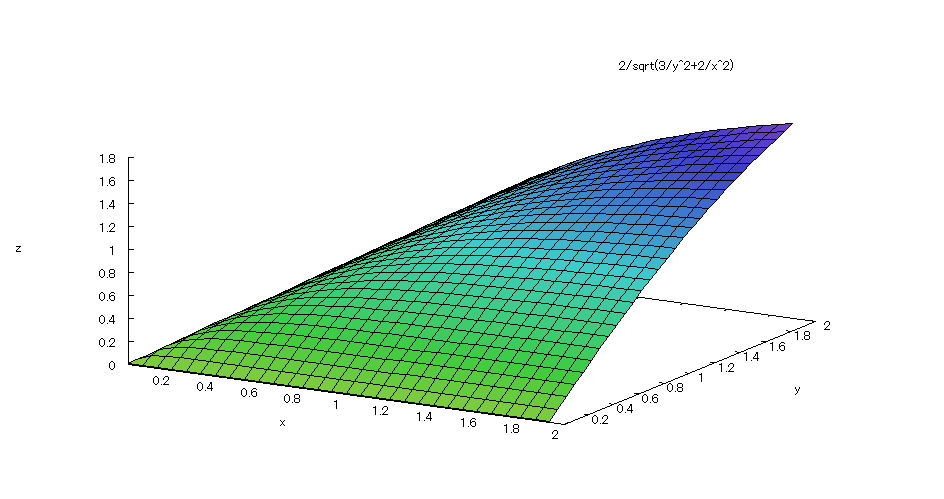 How to draw a graph @First , enter the first line of the above input express in half-width , and press the Shift key and Enter key at the same time. @Next , enter the second line in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 41z@Draw a graph of a 3D parameter. mTorusn |
mPnFunction expression @@@ @@@ @O QÎAO QÎ mQnInput formula @@@plot3d([cos(s)*(3+cos(t)),sin(s)*(3+cos(t)),sin(t)],[s,0,2*%pi],[t,0,2*%pi]); @@@ mRnDrawing result @@@@@ 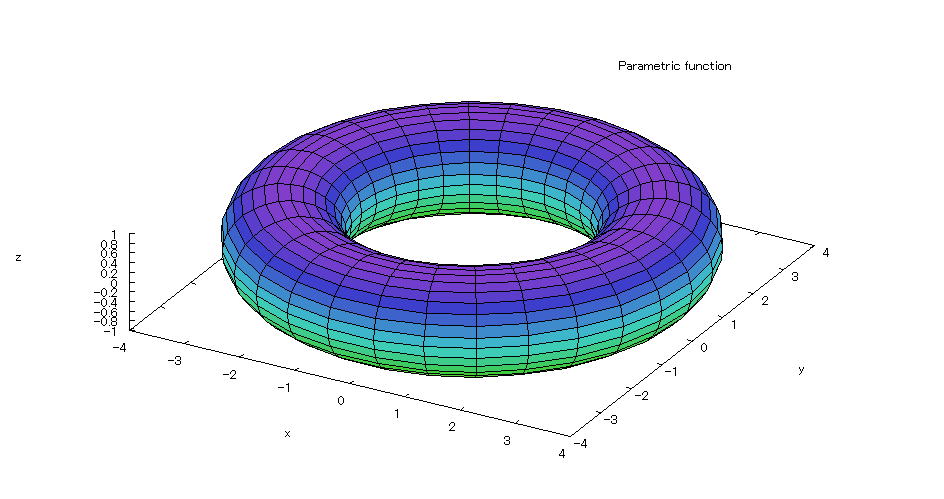 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 42z@Draw a graph of a 3D parameter. mAsteroidal spheren |
mPnFunction expression @@@ @@@ @O QÎAO QÎ mQnInput formula @@@plot3d([cos(s)^3*cos(t)^3,sin(s)^3*cos(t)^3,sin(t)^3],[s,0,2*%pi],[t,0,2*%pi]); @@@ mRnDrawing result @@@@@  How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 43z@Draw a graph of a 3D parameter. mHenneberg Minimal Surfacen |
mPnFunction expression @@@@ @@@@ @@@@ @@@ @ODR ODX@A@O QÎ mQnInput formula @@@plot3d([2*sinh(s)*cos(t)-(2/3)*sinh(3*s)*cos(3*t),2*sinh(s)*sin(t)-(2/3)*sinh(3*s) @@@@@@@@@@@@@@@@@@*sin(3*t),2*cosh(2*s)*cos(2*t)],[s,0.3,0.9],[t,0,2*%pi],[grid,4,72]); mRnDrawing result @@@@@ 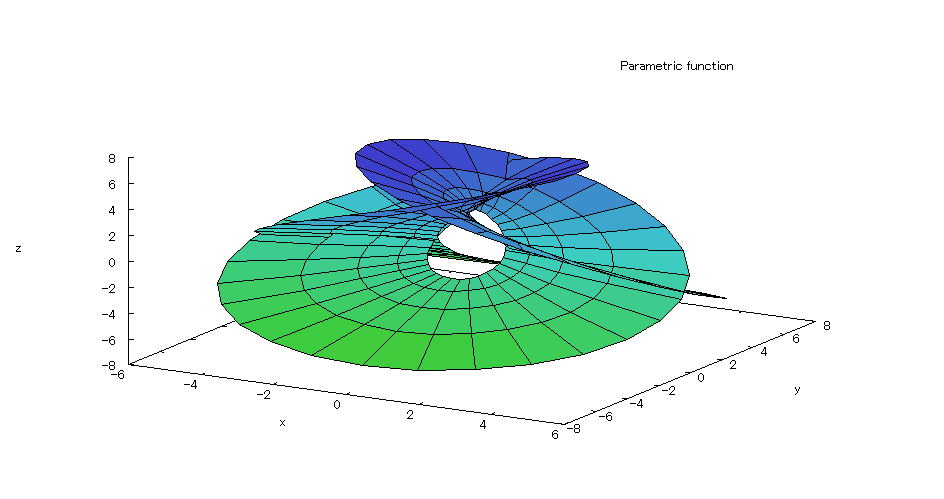 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 44z@Draw a graph of a 2D explicit function. mMake it easier to see by specifying the range of y-axis valuesn |
mPnFunction expression @@@@ mQnInput formula @@@plot2d(1/(x-1)+1,[x,-5,5],[y,-5,5]); mRnDrawing result @@@@@ 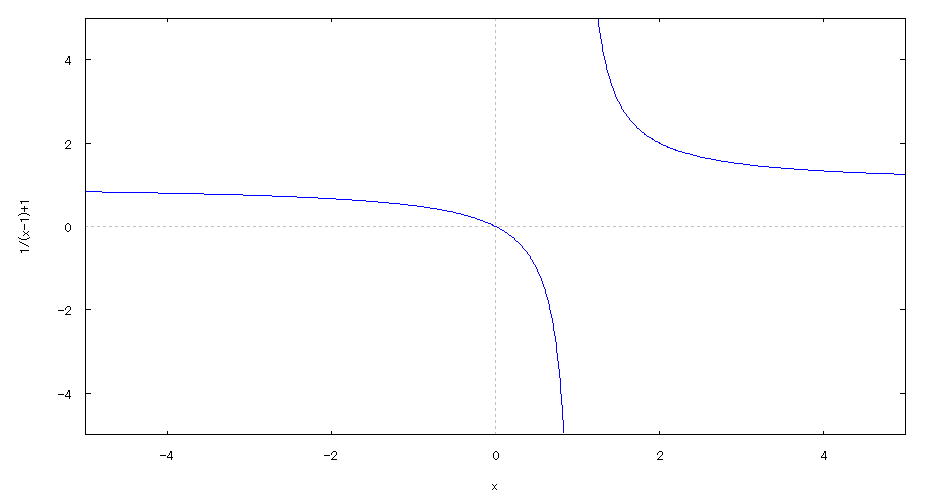 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 45z@Draw a graph of a 2D explicit function. mCompare with the Taylor expansion graph of the approximation formulan |
mPnFunction expression @@@@ mQnInput formula @@@plot2d([cos(x),1-x^2/2+x^4/24-x^6/720,1-x^2/2+x^4/24-x^6/720+x^8/40320, @@@@@@@@1-x^2/2+x^4/24-x^6/720+x^8/40320-x^10/3628800],[x,-2*%pi,2*%pi],[y,-5,5]); mRnDrawing result @@@@@ 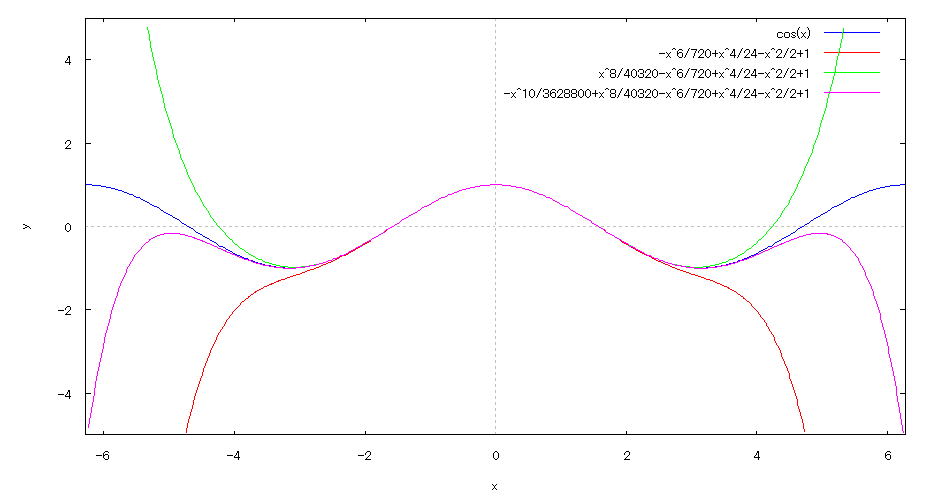 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 46z@Draw a graph of a 2D explicit function. mFind a number of real solutions to an equationn |
mPnEquation @@@@ mQnInput formula @@@plot2d([exp(x),3-x^2],[x,-2,2],[y,-1,4]); mRnDrawing result @@@@@ 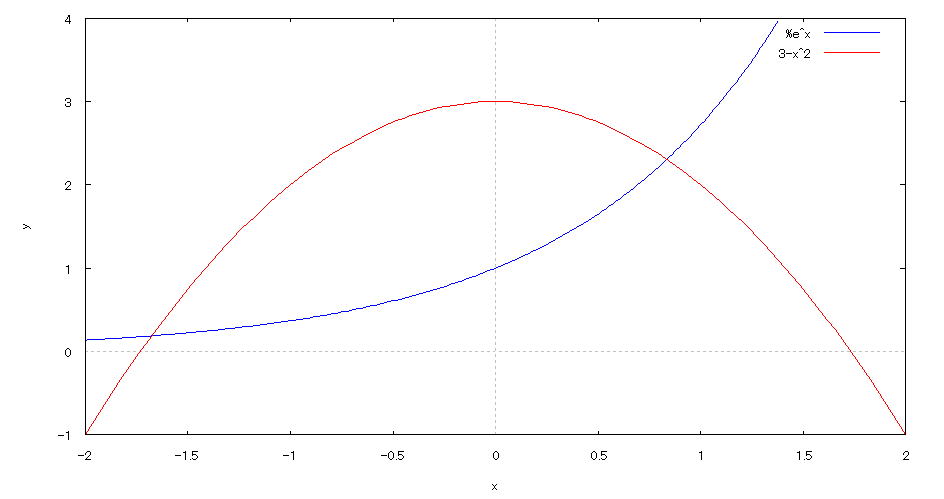 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @Since there are two points of intersection , we know that the equation has two real solutions. @ |
| @yExample 47z@Draw a graph of a 2D parameter. mCircleFDon't specify the number of divisionsn |
mPnFunction expression @@@@ mQnInput formula @@@ plot2d([parametric,cos(t),sin(t)],[t,0,2*%pi]); mRnDrawing result @@@@@ 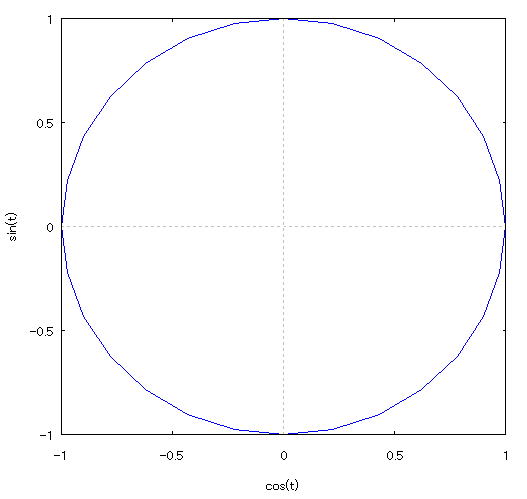 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 48z@Draw a graph of a 2D parameter. mCircleFspecify 15 divisionsn |
mPnFunction expression @@@@ mQnInput formula @@@ plot2d([parametric,cos(t),sin(t)],[t,0,2*%pi],[nticks,15]); mRnDrawing result @@@@@ 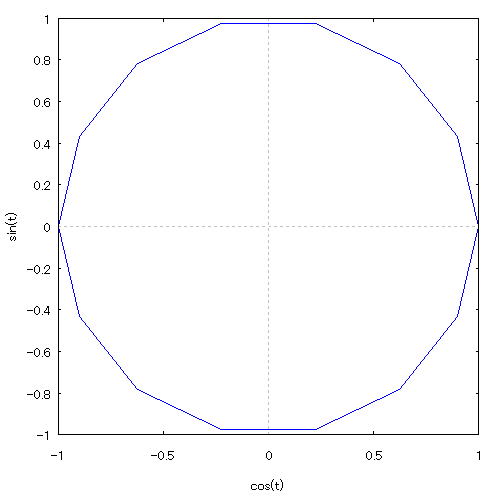 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 49z@Draw a graph of a 2D parameter. mCircleFspecify 100 divisionsn |
mPnFunction expression @@@@ mQnInput formula @@@ plot2d([parametric,cos(t),sin(t)],[t,0,2*%pi],[nticks,100]); mRnDrawing result @@@@@ 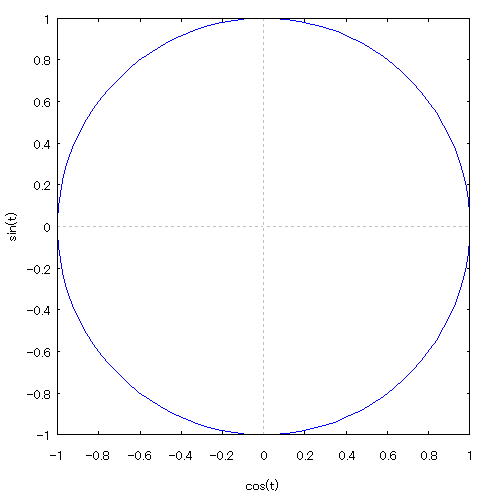 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 50z@Draw a graph of a 3D explicit function. mDo not specify the number of divisionsn |
mPnFunction expression @@@@ mQnInput formula @@@ plot3d(x^3-3*x*y^2,[x,-1,1],[y,-1,1]); mRnDrawing result @@@@@ 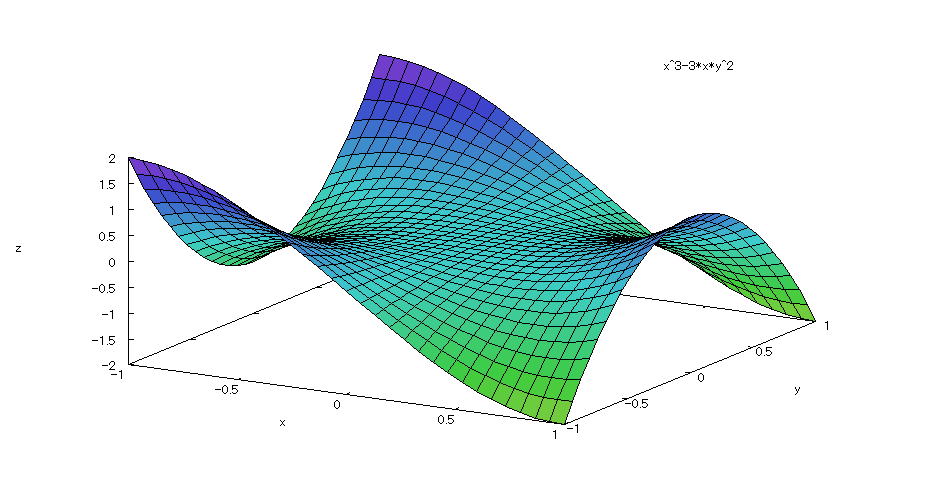 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 51z@Draw a graph of a 3D explicit function. mDon't specify the number of divisionsn |
mPnFunction expression @@@@ mQnInput formula @@@ plot3d((x^2*y)/(x^4+y^2),[x,-1,1],[y,-1,1]); mRnDrawing result @@@@@ 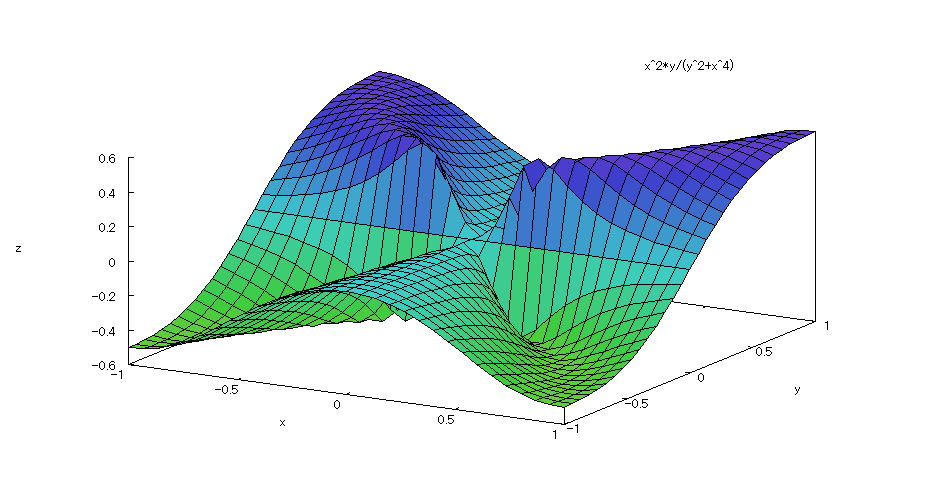 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 52z@Draw a graph of a 3D explicit function. mSpecify the number of divisionsn |
mPnFunction expression @@@@ mQnInput formula @@@ plot3d((x^2*y)/(x^4+y^2),[x,-1,1],[y,-1,1],[grid,100,100]); mRnDrawing result @@@@@ 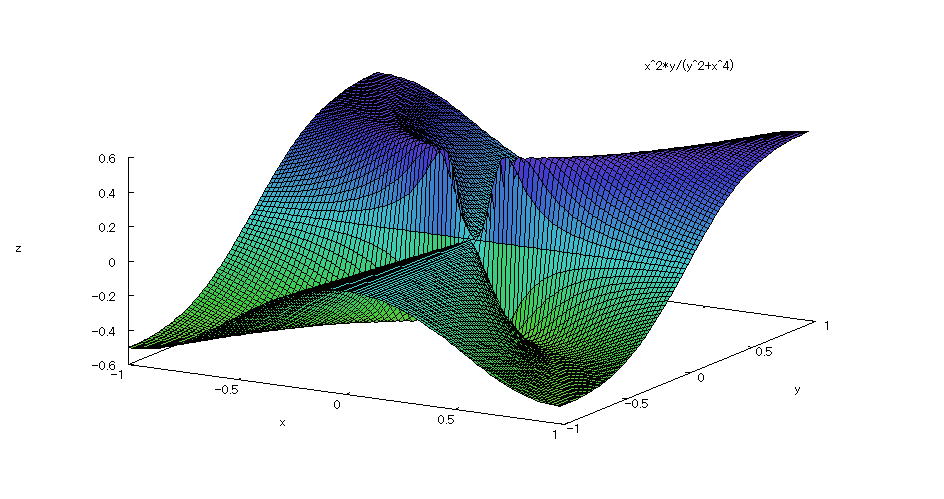 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 53z@Draw a graph of a 3D parameter. mSpherical surfaceFSpecify the number of divisionn |
mPnFunction expression @@@@ @@@@@O QÎAO QÎ mQnInput formula @@@ plot3d([cos(s)*cos(t),cos(s)*sin(t),sin(s)],[s,0,2*%pi],[t,0,2*%pi],[grid,50,50]); mRnDrawing result @@@@@ 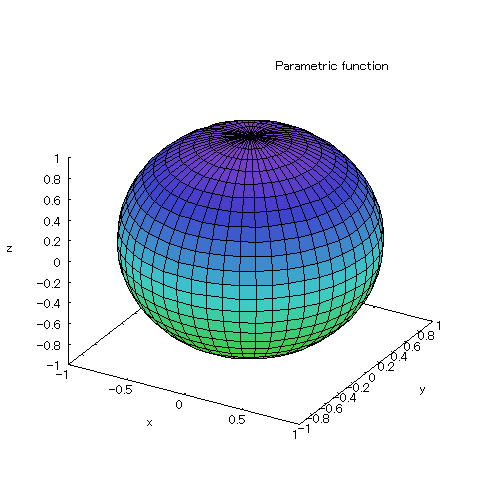 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 54z@Draw a graph of a 3D parameter. mAmazing shapes and equationsn |
mPnFunction expression @@@@ @@@@@@@@@@@@@@ @@@@ @@@@@@@@@@@@@@ @@@@ @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@O QÎAO QÎ mQnInput formula @@@ plot3d([3*cos(u)+5*cos(3*u)+(3*(cos(u)+5*cos(3*u))*cos(v))/(2*sqrt(234+90*cos(2*u))) @@@ -(3*cos(6*u)*(sin(u)+5*sin(3*u))*sin(v))/(2*sqrt(13+5*cos(2*u))*sqrt(22+5*cos(2*u) @@@ +9*cos(12*u))),3*sin(u)+5*sin(3*u)+(3*cos(v)*(sin(u)+5*sin(3*u)))/(2*sqrt(234+90*cos @@ @(2*u)))+(3*(5*cos(3*u)+cos(5*u)+cos(7*u)+5*cos(9*u))*sin(v))/(4*sqrt(13+5*cos(2*u)) @@@ *sqrt(22+5*cos(2*u)+9*cos(12*u))),3*sin(6*u)-(sqrt(13+5*cos(2*u))*sin(v))/(2*sqrt @@ @(22+5*cos(2*u)+9*cos(12*u)))],[u,0,2*%pi],[v,0,2*%pi],[grid,80,8]); mRnDrawing result @@@@@ 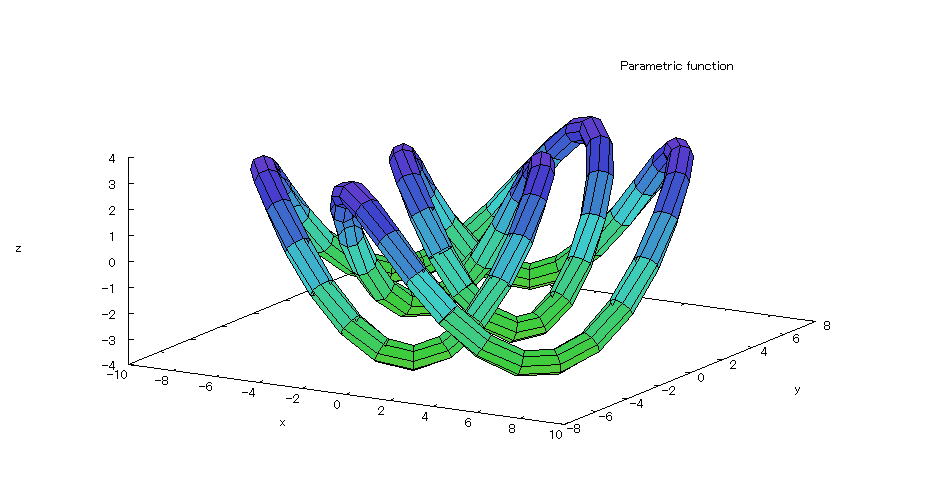 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 55z@Draw a graph of a 3D parameter. mRotating body 1n |
mPnRotating body @@@@A solid created by rotating the part enclosed by parabola y=x^2 , x=-3 , x=3 , the x-axis around the x-axis. mQnInput formula @@@ plot3d([t,t^2*cos(s),t^2*sin(s)],[t,-3,3],[s,0,2*%pi]); mRnDrawing result @@@@@ 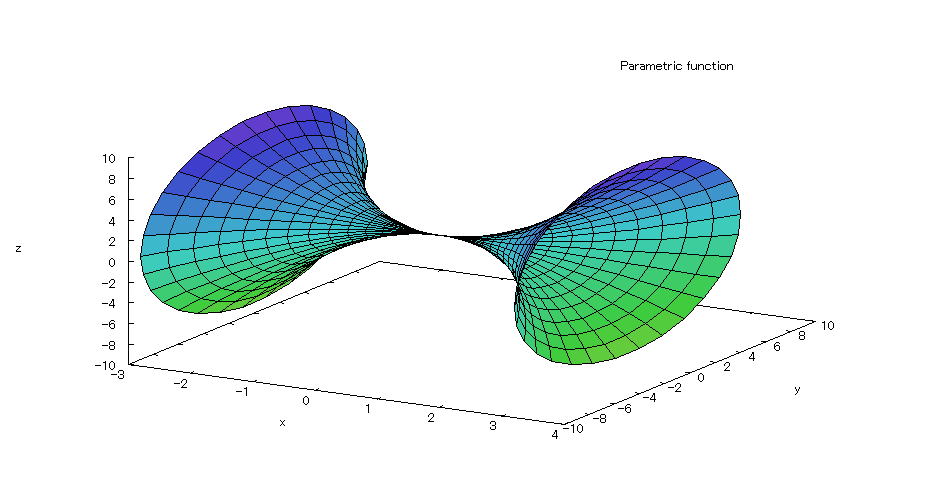 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 56z@Draw a graph of a 3D parameter. mRotating body 2n |
mPnRotating body @@@@A solid created by rotating the part enclosed by parabola x=ã , y=0 , y=9 , the y-axis around the y-axis. mQnInput formula @@@ plot3d([sqrt(t)*cos(s),t,sqrt(t)*sin(s)],[t,0,9],[s,0,2*%pi]); mRnDrawing result @@@@@ 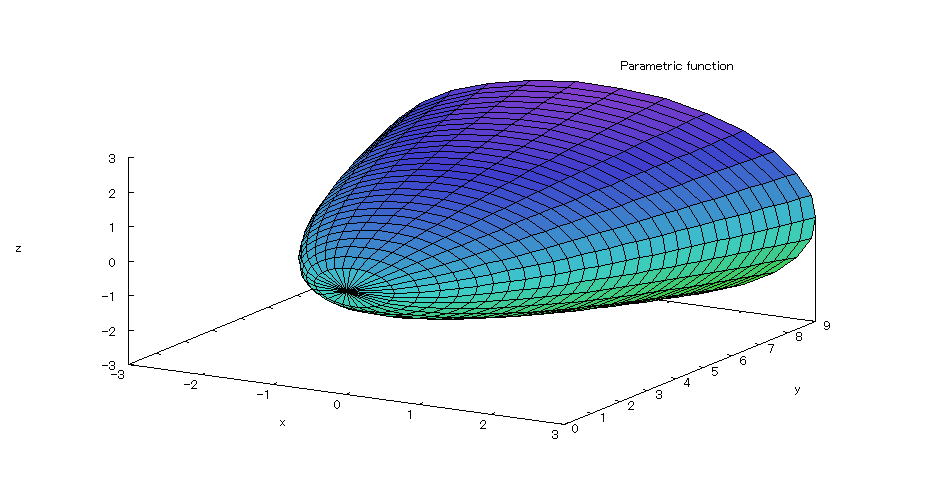 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 57z@Draw a graph of a 3D parameter. mRotating body 3n |
mPnRotating body @@@@A solid created by rotating the part enclosed by parabola y=x^2-2 , x=-3 , x=3 , the x-axis around the x-axis. mQnInput formula @@@ plot3d([t,(t^2-2)*cos(s),(t^2-2)*sin(s)],[t,-3,3],[s,0,2*%pi]); mRnDrawing result @@@@@ 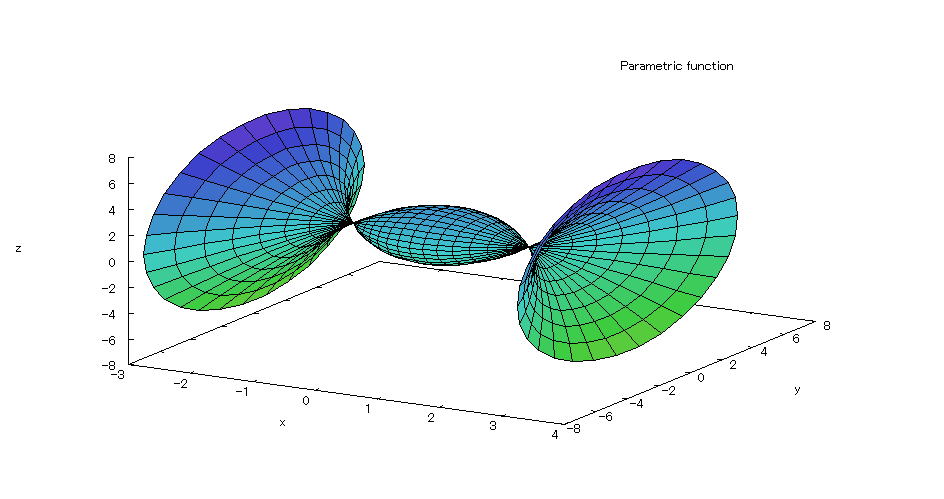 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 58z@Draw a graph of a 3D parameter. mRotating body 4n |
mPnRotating body @@@@A solid created by rotating the part enclosed by parabola y=x^2+2 , x=-3 , x=3 , the x-axis around the x-axis. mQnInput formula @@@ plot3d([t,(t^2+2)*cos(s),(t^2+2)*sin(s)],[t,-2,2],[s,0,2*%pi]); mRnDrawing result @@@@@ 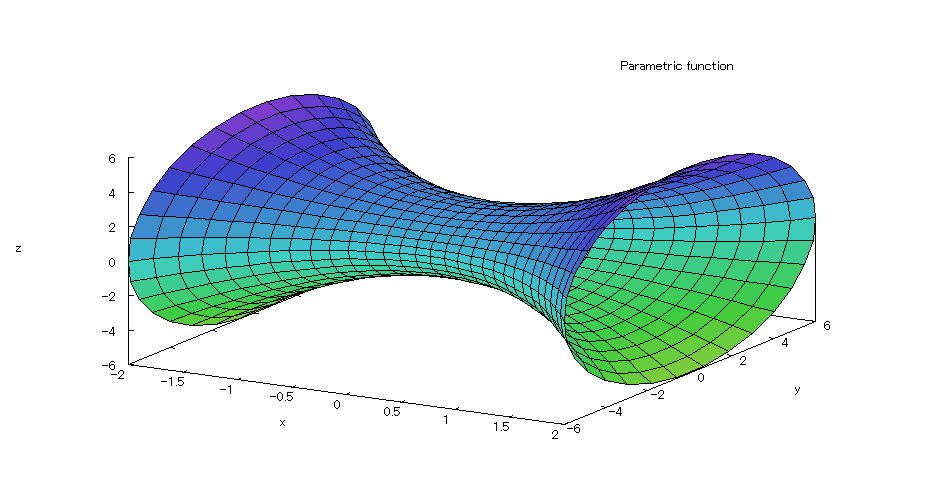 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 59z@Draw a graph of a 3D parameter. mRotating body 5n |
mPnRotating body @@@@A solid created by rotating circle: x^2+y^2=4 around the x-axis. mQnInput formula @@@ plot3d([t,sqrt(4-t^2)*cos(s),sqrt(4-t^2)*sin(s)],[t,-2,2],[s,0,2*%pi]); mRnDrawing result @@@@@ 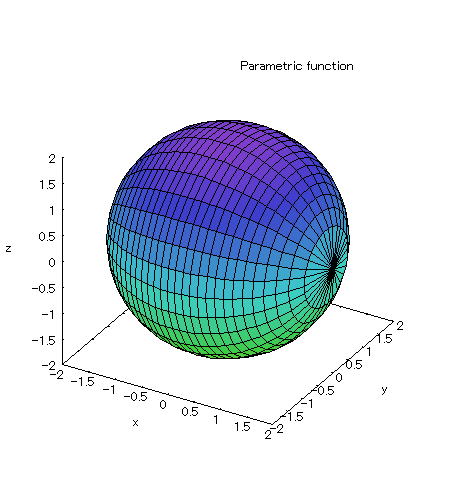 How to draw a graph @As in the above input formula , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 60z@Approximation of expressions by Taylor Expansion mn |
mPnInput expression for Taylor Expansion of sinx @@@@taylor(sin(x),x,0,12); mQnDeployment result @@@ mRnAn input expression that draws the graph of and its approximation @@@plot2d([sin(x),x-x^3/6+x^5/120-x^7/5040+x^9/362880-x^11/39916800],[x,-10,10],[y,-1.2,1.2]); mSnDrawing result @@@@@ 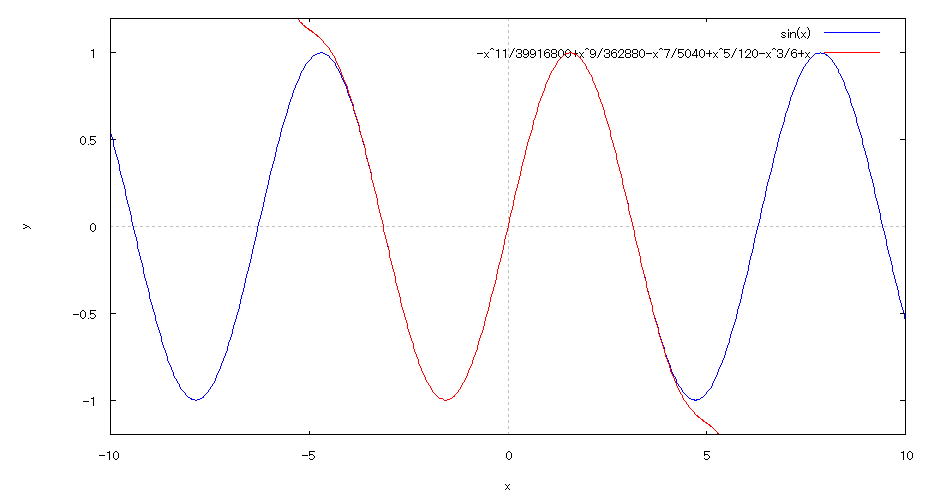 How to draw a graph @ As in the input formula in [3] above , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 61z@Approximation of expressions by Taylor Expansion mn |
mPnInput expression for Taylor Expansion of cosx @@@@taylor(cos(x),x,0,12); mQnDeployment result @@@ mRnAn input expression that draws the graph of and its aaproximation @@@plot2d([cos(x),1-x^2/2+x^4/24-x^6/720+x^8/40320-x^10/3628800+x^12/479001600] @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@,[x,-10,10],[y,-1.2,1.2]); mSnDrawing result @@@@@ 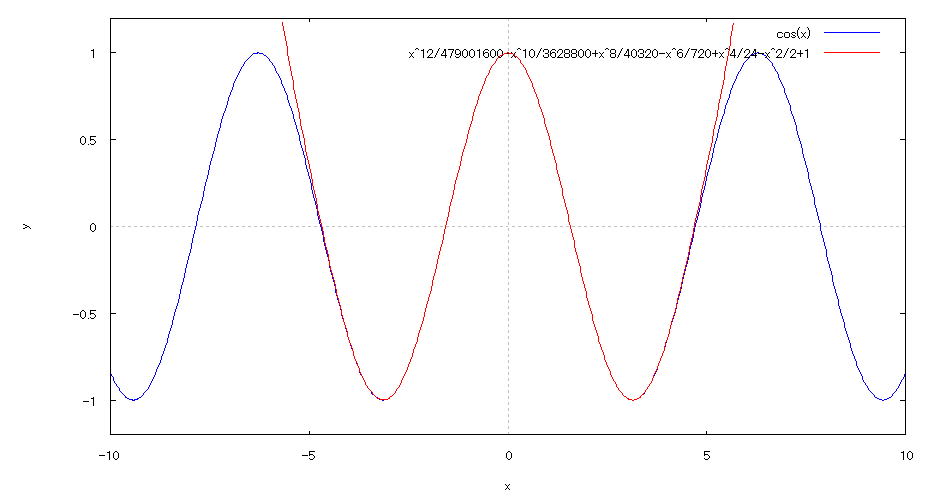 How to draw a graph @ As in the input formula in [3] above , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 62z@Approximation of expressions by Taylor Expansion |
mPnInut expression for Taylor Expansion of e^x @@@@taylor(exp(x),x,0,6); mQnDeployment result @@@ 1+x+x^2/2+x^3/6+x^4/24+x^5/120+... mRn An input expression that draws the graph of @@@@plot2d([exp(x),1+x+x^2/2+x^3/6+x^4/24+x^5/120],[x,-3,3],[y,0,5]); mSnDrawing result @@@@@ 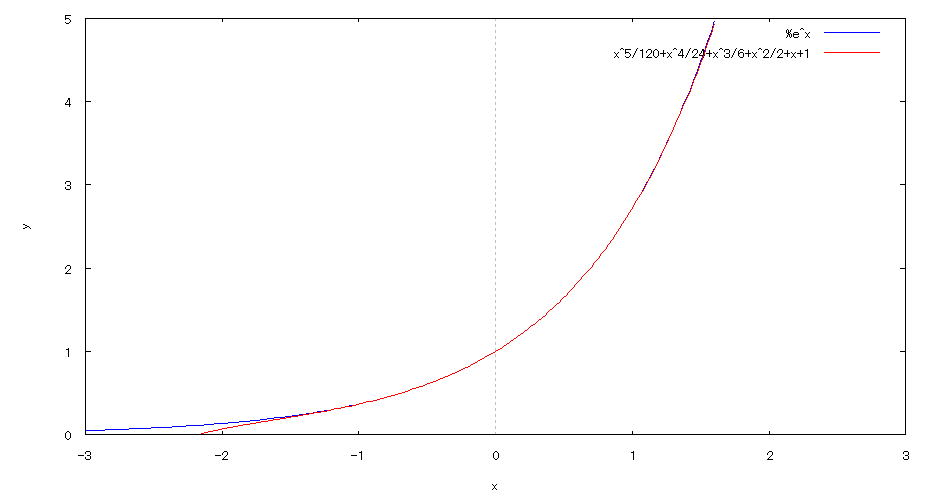 How to draw a graph @ As in the input formula in [3] above , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yExample 63z@Prove Euler's formula |
mPnInput expression for Taylor Expansion of @@@@taylor((x),x,0,12); mQnTaylor Expansion result of @@@ mRnInput expression for Taylor Expansion of cos @@@@taylor(cos(x),x,0,12); mSnTaylor Expansion result of cos @@@@ mTnInput expression for Taylor Expansion of@ @@@@taylor(exp(%i*x),x,0,12); mUnTaylor Expansion result of@ @@@ @@@@|||B @@@Above , from @ , A , B @@@@@ @@@@@@@@@@@@@@@@@@@ @@@@@@@@ { @@@Therefore , How to display the expansion formula @ As in the input formulas in [1] , [3] , [5] above , enter all in half-width and press the Shift key and Enter key at the same time. @ |
| @yProblem 1z@How many digits is 2^30 in integer ? However , (10C2)0.3010. |
| @This problem always comes up in common logarithms. @If you teach in the order of @¨A¨B¨C below , you can make the number of digits more specific. @Display 2^30 , 2^50 , 2^100 , 3^30 , 3^50 , and 3^100 computed by l and count the number of digits. ATeach how to find the number of digits by using common rogarithms. BFind the number of digits in 2^30 , 2^50 , 2^100 , 3^30 , 3^50 , and 3^100 using common logarithms and comfirm that it matches the number of digits you just counted. CTouching on how to count large numbers. Below are the results caluculated by Maxima. @2^301073741824 @2^501125899906842624 @2^1001267650600228229401496703205376 @3^30205891132094649 @3^50717897987691852588770249 @3^100515377520732011331036461129765621272702107522001 How to use "l" @For example , to calculate 2^30 @Enter 2^30@in half-width , and press the Shift key and Enter key at the same time. |
| @yProblem 2z@Expand i{j^3@and@i{{j^2@ |
| @Expanding i{j^3@or@i{{j^2@doesn't surprise you much. @I wondered if it would be possible to have a class that surprises and impresses students by having Maxima calculate and display the expansion of i{j^50 and i{{j^20 in the introduction of the expansion of equations. Below is the result of expansion by Maxima @@i{j^50 @b^50+50*a*b^49+1225*a^2*b^48+19600*a^3*b^47+230300*a^4*b^46+2118760*a^5*b^45 @@+15890700*a^6*b^44+99884400*a^7*b^43+536878650*a^8*b^42+2505433700*a^9*b^41 @@+10272278170*a^10*b^40+37353738800*a^11*b^39+121399651100*a^12*b^38 @@+354860518600*a^13*b^37+937845656300*a^14*b^36+2250829575120*a^15*b^35 @@+4923689695575*a^16*b^34+9847379391150*a^17*b^33+18053528883775*a^18*b^32 @@+30405943383200*a^19*b^31+47129212243960*a^20*b^30+67327446062800*a^21*b^29 @@+88749815264600*a^22*b^28+108043253365600*a^23*b^27+121548660036300*a^24*b^26 @@+126410606437752*a^25*b^25+121548660036300*a^26*b^24+108043253365600*a^27*b^23 @@+88749815264600*a^28*b^22+67327446062800*a^29*b^21+47129212243960*a^30*b^20 @@+30405943383200*a^31*b^19+18053528883775*a^32*b^18+9847379391150*a^33*b^17 @@+4923689695575*a^34*b^16+2250829575120*a^35*b^15+937845656300*a^36*b^14 @@+354860518600*a^37*b^13+121399651100*a^38*b^12+37353738800*a^39*b^11 @@+10272278170*a^40*b^10+2505433700*a^41*b^9+536878650*a^42*b^8+99884400*a^43*b^7 @@+15890700*a^44*b^6+2118760*a^45*b^5+230300*a^46*b^4+19600*a^47*b^3+1225*a^48*b^2 @@+50*a^49*b+a^50 @@i{{j^20 @c^20+20*b*c^19+20*a*c^19+190*b^2*c^18+380*a*b*c^18+190*a^2*c^18+1140*b^3*c^17 @@+3420*a*b^2*c^17+3420*a^2*b*c^17+1140*a^3*c^17+4845*b^4*c^16+19380*a*b^3*c^16 @@+29070*a^2*b^2*c^16+19380*a^3*b*c^16+4845*a^4*c^16+15504*b^5*c^15+77520*a*b^4*c^15 @@+155040*a^2*b^3*c^15+155040*a^3*b^2*c^15+77520*a^4*b*c^15+15504*a^5*c^15 @@+38760*b^6*c^14+232560*a*b^5*c^14+581400*a^2*b^4*c^14+775200*a^3*b^3*c^14 @@+581400*a^4*b^2*c^14+232560*a^5*b*c^14+38760*a^6*c^14+77520*b^7*c^13 @@+542640*a*b^6*c^13+1627920*a^2*b^5*c^13+2713200*a^3*b^4*c^13+2713200*a^4*b^3*c^13 @@+1627920*a^5*b^2*c^13+542640*a^6*b*c^13+77520*a^7*c^13+125970*b^8*c^12 @@+1007760*a*b^7*c^12+3527160*a^2*b^6*c^12+7054320*a^3*b^5*c^12 @@+8817900*a^4*b^4*c^12+7054320*a^5*b^3*c^12+3527160*a^6*b^2*c^12 @@+1007760*a^7*b*c^12+125970*a^8*c^12+167960*b^9*c^11+1511640*a*b^8*c^11 @@+6046560*a^2*b^7*c^11+14108640*a^3*b^6*c^11+21162960*a^4*b^5*c^11 @@+21162960*a^5*b^4*c^11+14108640*a^6*b^3*c^11+6046560*a^7*b^2*c^11 @@+1511640*a^8*b*c^11+167960*a^9*c^11+184756*b^10*c^10+1847560*a*b^9*c^10 @@+8314020*a^2*b^8*c^10+22170720*a^3*b^7*c^10+38798760*a^4*b^6*c^10 @@+46558512*a^5*b^5*c^10+38798760*a^6*b^4*c^10+22170720*a^7*b^3*c^10 @@+8314020*a^8*b^2*c^10+1847560*a^9*b*c^10+184756*a^10*c^10+167960*b^11*c^9 @@+1847560*a*b^10*c^9+9237800*a^2*b^9*c^9+27713400*a^3*b^8*c^9 @@+55426800*a^4*b^7*c^9+77597520*a^5*b^6*c^9+77597520*a^6*b^5*c^9 @@+55426800*a^7*b^4*c^9+27713400*a^8*b^3*c^9+9237800*a^9*b^2*c^9 @@+1847560*a^10*b*c^9+167960*a^11*c^9+125970*b^12*c^8+1511640*a*b^11*c^8 @@+8314020*a^2*b^10*c^8+27713400*a^3*b^9*c^8+62355150*a^4*b^8*c^8 @@+99768240*a^5*b^7*c^8+116396280*a^6*b^6*c^8+99768240*a^7*b^5*c^8 @@+62355150*a^8*b^4*c^8+27713400*a^9*b^3*c^8+8314020*a^10*b^2*c^8 @@+1511640*a^11*b*c^8+125970*a^12*c^8+77520*b^13*c^7+1007760*a*b^12*c^7 @@+6046560*a^2*b^11*c^7+22170720*a^3*b^10*c^7+55426800*a^4*b^9*c^7 @@+99768240*a^5*b^8*c^7+133024320*a^6*b^7*c^7+133024320*a^7*b^6*c^7 @@+99768240*a^8*b^5*c^7+55426800*a^9*b^4*c^7+22170720*a^10*b^3*c^7 @@+6046560*a^11*b^2*c^7+1007760*a^12*b*c^7+77520*a^13*c^7+38760*b^14*c^6 @@+542640*a*b^13*c^6+3527160*a^2*b^12*c^6+14108640*a^3*b^11*c^6 @@+38798760*a^4*b^10*c^6+77597520*a^5*b^9*c^6+116396280*a^6*b^8*c^6 @@+133024320*a^7*b^7*c^6+116396280*a^8*b^6*c^6+77597520*a^9*b^5*c^6 @@+38798760*a^10*b^4*c^6+14108640*a^11*b^3*c^6+3527160*a^12*b^2*c^6 @@+542640*a^13*b*c^6+38760*a^14*c^6+15504*b^15*c^5+232560*a*b^14*c^5 @@+1627920*a^2*b^13*c^5+7054320*a^3*b^12*c^5+21162960*a^4*b^11*c^5 @@+46558512*a^5*b^10*c^5+77597520*a^6*b^9*c^5+99768240*a^7*b^8*c^5 @@+99768240*a^8*b^7*c^5+77597520*a^9*b^6*c^5+46558512*a^10*b^5*c^5 @@+21162960*a^11*b^4*c^5+7054320*a^12*b^3*c^5+1627920*a^13*b^2*c^5 @@+232560*a^14*b*c^5+15504*a^15*c^5+4845*b^16*c^4+77520*a*b^15*c^4 @@+581400*a^2*b^14*c^4+2713200*a^3*b^13*c^4+8817900*a^4*b^12*c^4 @@+21162960*a^5*b^11*c^4+38798760*a^6*b^10*c^4+55426800*a^7*b^9*c^4 @@+62355150*a^8*b^8*c^4+55426800*a^9*b^7*c^4+38798760*a^10*b^6*c^4 @@+21162960*a^11*b^5*c^4+8817900*a^12*b^4*c^4+2713200*a^13*b^3*c^4 @@+581400*a^14*b^2*c^4+77520*a^15*b*c^4+4845*a^16*c^4+1140*b^17*c^3 @@+19380*a*b^16*c^3+155040*a^2*b^15*c^3+775200*a^3*b^14*c^3 @@+2713200*a^4*b^13*c^3+7054320*a^5*b^12*c^3+14108640*a^6*b^11*c^3 @@+22170720*a^7*b^10*c^3+27713400*a^8*b^9*c^3+27713400*a^9*b^8*c^3 @@+22170720*a^10*b^7*c^3+14108640*a^11*b^6*c^3+7054320*a^12*b^5*c^3 @@+2713200*a^13*b^4*c^3+775200*a^14*b^3*c^3+155040*a^15*b^2*c^3 @@+19380*a^16*b*c^3+1140*a^17*c^3+190*b^18*c^2+3420*a*b^17*c^2 @@+29070*a^2*b^16*c^2+155040*a^3*b^15*c^2+581400*a^4*b^14*c^2 @@+1627920*a^5*b^13*c^2+3527160*a^6*b^12*c^2+6046560*a^7*b^11*c^2 @@+8314020*a^8*b^10*c^2+9237800*a^9*b^9*c^2+8314020*a^10*b^8*c^2 @@+6046560*a^11*b^7*c^2+3527160*a^12*b^6*c^2+1627920*a^13*b^5*c^2 @@+581400*a^14*b^4*c^2+155040*a^15*b^3*c^2+29070*a^16*b^2*c^2 @@+3420*a^17*b*c^2+190*a^18*c^2+20*b^19*c+380*a*b^18*c+3420*a^2*b^17*c @@+19380*a^3*b^16*c+77520*a^4*b^15*c+232560*a^5*b^14*c+542640*a^6*b^13*c @@+1007760*a^7*b^12*c+1511640*a^8*b^11*c+1847560*a^9*b^10*c @@+1847560*a^10*b^9*c+1511640*a^11*b^8*c+1007760*a^12*b^7*c @@+542640*a^13*b^6*c+232560*a^14*b^5*c+77520*a^15*b^4*c+19380*a^16*b^3*c @@+3420*a^17*b^2*c+380*a^18*b*c+20*a^19*c+b^20+20*a*b^19+190*a^2*b^18 @@+1140*a^3*b^17+4845*a^4*b^16+15504*a^5*b^15+38760*a^6*b^14 @@+77520*a^7*b^13+125970*a^8*b^12+167960*a^9*b^11+184756*a^10*b^10 @@+167960*a^11*b^9+125970*a^12*b^8+77520*a^13*b^7+38760*a^14*b^6 @@+15504*a^15*b^5+4845*a^16*b^4+1140*a^17*b^3+190*a^18*b^2+20*a^19*b+a^20 How to use "Maxima" @For example , when expanding (a+b)^50 @Enter expand((a+b)^50)@in half-width , and press the Shift key and Enter key at the same time. |
| @yProblem 3z@Solve the higher equation ^3{Q^2{Q{PO. |
| @The high-level equation handled in high school is a form that can be solved
by using factor decomposition or the like , or can be solved as x^2=t or
the like. @Solve the cubic equation ax^3+bx^2+cx+d=0 in "Maxima". Then the formula of the cubic equation is displayed. Will the students be surprised and impressed ? @Also , if you solve the cubic equation ^3|U|POO@, and the quartic equation ^4{R^3|PW^2{U|TO@using Maxima and display them , the complexity of the solution should surprise the students. How to use "l" @For example , when solving ax^3+bx^2+cx+d=0 @Enter solve(*^3{*^2{*{O,x)@in half-width , press the Shift key and Enter key at the same time. |
| @The result of letting "Maxima"@solve a cubic equation ^3{^2{{O |
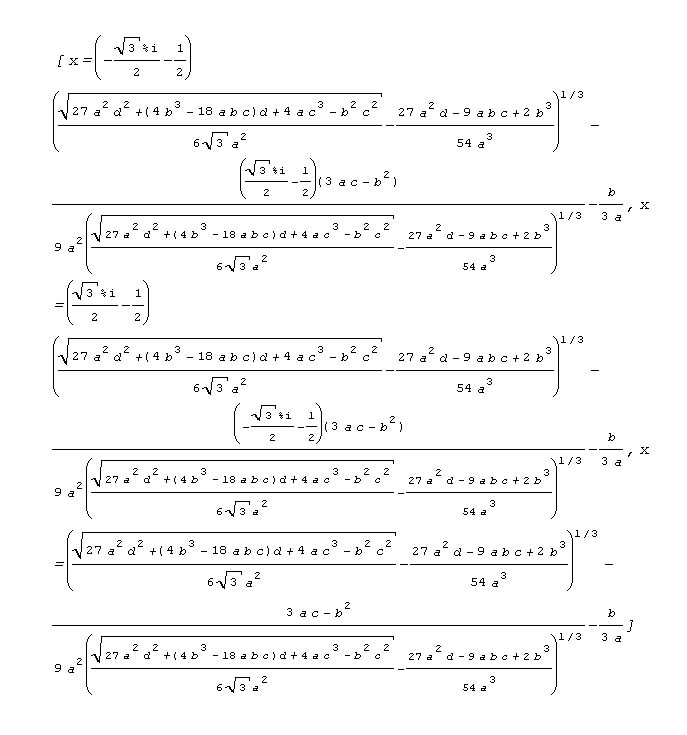 |
| @The result of letting "Maxima" solve a cubic equation @^3|U|POO |
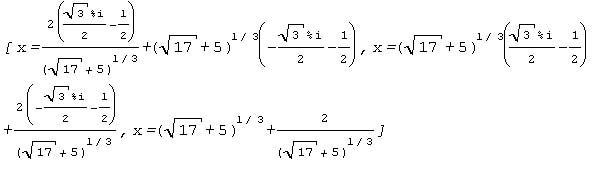 |
| @yProblem 4z@Factor |{|P |
| @This is a problem of cleaning up and factoring for one character. @If we let Maxima solve more complex factorizations and display them , I wondered if it would be possible to create a class that surprises and impresses the students. @Students would be surprised if@({{)({{)| , (|)^3{(|)^3{(|)^3 , ^3{^3{^3|R , and ({)({)({){ were factored instantly , using Maxima displayed. Below is the result of following with "Maxima" @(a+b+c)(bc+ca+ab)-abc = (b+a)(c+a)(c+b) @(b-c)^3+(c-a)^3+(a-b)^3 = 3(b-a)(c-a)(c-b) @a^3+b^3+c^3-3*a*b*c = (c+b+a)(c^2-b*c-a*c+b^2-a*b+a^2) @(b+c)(c+a)(a+b)+abc = (c+b+a)(bc+ac+ab) How to use "Maxima" @For example , when factoring (a+b+c)(bc+ca+ab)-abc @ @Enter factor((a+b+c)*(b*c+c*a+a*b)-a*b*c)@in half-width , and press the Shift key and Enter key at the same time. |
| @yProblem 5z@Differentiate ({V^2)^(1/3).@ |
| @I wonder if I could create a class that surprise and impress students
by searching for more complex expressions in workbooks and using "Maxima"
to differentiate them and display them. Below is the result of differentiating with "Maxima" @{({V^2)^(1/3)}f = (14*x+1)/(3*(7*x^2+x)^(2/3)) How to use "l" @For example , when differentiating ({V^2)^(1/3) @Enter diff((x+7*x^2)^(1/3), x)@in half-width , and press the Shift key and Enter key at the same time. |
| @yProblem 6z@Integrate ã(P{T)@ |
| @I wonder if I could create a class that surprises and impresses by searching
for more complex expressions in workbooks and using "Maxima"
to integrate them and display them. Below is the result of integrating with "Maxima". çã(P{T) = (2*(5*x+1)^(3/2))/15 How to use "l" @For example , when integrating@ã(P{T) @Enter integrate(sqrt(1+5*x) , x)@in half-width , and press the Shift key and Enter key at the same time. |
| @Formula manipulation software "Maxima" | @Formula manipulation software "wxl" |
| @Click on the formula manipulation software "l" above to open Maxima's official website. @Click Download on the left menue of this wxMaxima official site. @Next , click Sourceforge download page. @And , click Maxima Windows. @Furthermore , click 5.26.0-Windows. @Then , ckick maxima-5.26.0.exe to download "maxima 5.26.0.exe". @Double-click "maxima-5.26.0.exe" downloaded to launch the Maxima installer. @After that , follow the instructions on the screen to install. However , 5.26.0 in "maxima-5.26.0.exe" represents the version. (2/12/2012) |
| @Since the icon of "wxMaxima" is created on the desktop , double-click it to start "Maxima". |
| @You can download a Maxima data file "MSample.wxm" containing
all the sample programs shown on this website. @Click the data file "MSamp.lzh" and save it to your desktop or other location. @Unzip the downloaded file "MSamp.lzh" , put the cursor on the input expression you want to excute , and press the Shift key and Enter key at the same time to excute it. Of course , "Maxima" must be installed before that. |
| Data file "MSamp.wxm" |